Shorelark

В этом туториале мы создадим симуляцию эволюции с помощью нейронной сети и генетического алгоритма.

Я расскажу вам, как работают простая нейронная сеть и генетический алгоритм, затем мы реализуем их на Rust и скомпилируем приложение в WebAssembly.

Предполагается, что вы немного знакомы с Rust, остальное я постараюсь объяснить.

• Исходный код проекта
• Демо приложения

Часть 1

Проект

Начнем с того, что мы будем симулировать.

Основная идея состоит в том, что у нас есть двумерная доска, представляющая мир:

Этот мир состоит из птиц (поэтому проект называется "Shorelark" (береговой жаворонок)):

...и еды (абстрактной, богатой белком и клетчаткой):

Каждая птица обладает зрением, позволяющим обнаруживать еду:

...и мозгом, управляющим ее телом (скоростью и вращением).

Вместо кодирования определенного поведения птиц (например, "иди к ближайшей еде, находящейся в поле зрения"), мы сделаем так, что они будут учиться и эволюционировать.

Мозг

Условно, мозг - это не что иное, как функция от некоторых входных данных к некоторым выходных данным, например:

f(зрение, обоняние, слух, вкус, осязание) = (речь, движение)

Поскольку у наших птиц есть только зрение, их мозг может быть упрощен до:

f(зрение) = движение

Математически мы можем представить входные данные этой функции (биологического глаза) как список чисел, где каждое число (биологический фоторецептор) описывает, как близко находится объект (еда):

(0.0 - в поле зрения нет объектов, 1.0 - объект находится прямо напротив нас)

Наши птицы не видят цвет (для простоты) - вы можете использовать трассировку лучей, чтобы сделать глаза более реалистичными.

В качестве выходных данных функция будет возвращать кортеж (Δspeed, Δrotation).

Например, сообщение от мозга (0.1, 45) означает "тело, ускорься на 0.1 единицы и повернись на 45 градусов по часовой стрелке", а сообщение (0.0, 0) означает "тело, продолжай в том же духе".

Важно, чтобы использовались относительные значения (delta speed и delta rotation), поскольку наш мозг не будет знать о локации и вращении относительно мира - передача этой информации усложнит мозг без реальной выгоды.

Получается, что мозг - это f(глаза), верно? Но f(глаза) = что?

Нейронная сеть: введение

Полагаю, вы знаете, что мозг состоит из нейронов, соединенных синапсами:

Синапсы переносят электрический и химический сигналы между нейронами, а нейроны "решают", должен определенный сигнал передаваться дальше или блокироваться; в конечном счете, это позволяет людям распознавать буквы, есть брюссельскую капусту и писать злобные комментарии в Твиттере.

Из-за внутренней сложности биологические нейронные сети не самая легкая вещь для симуляции, что заставило некоторых умных людей изобрести класс математических структур под названием "искусственные нейронные сети", которые позволяют до некоторой степени аппроксимировать работу мозга с помощью математики.

Искусственные нейронные сети (далее - просто нейронные сети) играют важную роль в обобщении наборов данных (например, изучая, как выглядит кошка), поэтому они широко используются в распознавании лиц (например, для камер), языковом переводе (например, для GNMT) и - в нашем случае - для управления цветными пикселями.

Сеть, которую мы будем использовать, называется "нейронной сетью прямого распространения" (feedforward neural network, FFNN)...

FFNN иногда называют многослойными перцептронами. Они являются одним из строительных блоков сверточных нейронных сетей, таких как DeepDream.

...и выглядит так:

Это макет FFNN с 5 синапсами и 3 нейронами, организованными в 2 слоя: входной (слева) и выходной (справа).

Между этими слоями могут существовать дополнительные слои, которые называются "скрытыми" - они улучшают способность сети к интерпретации входных данных (чем больше мозг, тем "большую абстракцию" он способен понять, до определенной степени).

Похожий процесс происходит в нашей зрительной коре.

В отличие от биологических нейронных сетей (которые переносят электрические сигналы), FFNN принимают некоторые числа и пропускают их через несколько слоев. Числа на последнем слое определяют ответ сети.

Например, если мы скормили сети сырые пиксели изображения, она может ответить следующим:

• 0.0 - это изображение не содержит рыжего кота, поедающего лазанью
• 0.5 - это изображение может содержать рыжего кота, поедающего лазанью
• 1.0 - это изображение точно содержит рыжего кота, поедающего лазанью

Сеть также может возвращать несколько значений (количество выходных значений равняется количеству нейронов в выходном слое):

• (0.0, 0.5) - это изображение не содержит рыжего кота, но может содержать лазанью
• (0.5, 0.0) - это изображение может содержать рыжего кота, но не содержит лазанью

Значение входных и выходных чисел определяется нами - мы готовим так называемый набор обучающих данных ("при получении этого изображения, ты должна возвращать 1.0", "при получении этого изображения, ты должна возвращать 0.0").

Вы даже можете создать сеть для определения зрелых яблок - виды сетей ограничены только вашим воображением.

Двигаемся дальше.

Нейронные сети: глубокое погружение

FFNN зиждется на 2 столпах: нейронах и синапсах.

Нейрон (обычно изображаемый в виде круга) принимает некоторые входные значения, обрабатывает их и возвращает некоторое выходное значение - каждый нейрон имеет минимум один вход и максимум один выход:

Один нейрон с тремя синапсами

Кроме того, каждый нейрон имеет смещение (bias):

Один нейрон с тремя синапсами и смещением

Смещение - это как инструкция if нейрона - оно позволяет нейрону оставаться неактивным (возвращать нуль) до тех пор, пока входное значение не будет выше (строго) смещения. Формально, мы говорим, что смещение позволяет регулировать порог активации (activation threshold) нейрона.

Предположим, что у нас есть нейрон с тремя входными значениями, каждое значение определяет, видит нейрон лазанью (1.0) или нет (0.0). Если мы хотим, чтобы нейрон активировался при виде двух лазаний, мы просто создаем нейрон со смещением -1.0. Таким образом, "обычным" состоянием нейрона будет -1.0 (покой), при виде одной лазаньи - 0.0 (все еще покой), при виде двух лазаний - 1.0 (активация, вуаля).

Если вам не нравится моя метафора с лазаньей, вот математическое объяснение.

Помимо нейронов, у нас есть синапсы - сети, соединяющие выход одного нейрона с входном другого нейрона. Каждый синапс имеет вес (weight):

Один нейрон с тремя синапсами с весами

Вес - это фактор (отсюда x перед каждым числом, подчеркивающий его мультипликативную природу), поэтому вес:

• 0.0 означает, что синапс фактически мертв (он не передает информацию от одного нейрона другому)
• 0.3 означает, что если нейрон А возвращает 0.7, нейрон B получит 0.7 * 0.3 ~= 0.2
• 1.0 означает, что синапс фактически является транзитным - если нейрон A возвращает 0.7, нейрон B получит 0.7 * 1.0 = 0.7

Вернемся к нашей сети и заполним недостающие веса и смещения произвольными числами:

Красиво, не правда ли?

Посмотрим, что наша сеть думает о, скажем, (0.5, 0.8):

Напомню, что нас интересует выходное значение самого правого нейрона (это наш выходной слой). Поскольку он зависит от двух предыдущих нейронов (из входного слоя), начнем с них.

Сначала сфокусируемся на верхнем левом нейроне - для вычисления его выходного значения начнем с вычисления взвешенной суммы (weighted sum) его входных значений:

0.5 * 0.2 = 0.1

...затем добавляем смещение:

0.1 - 0.3 = -0.2

...и фиксируем (clamp) это значение с помощью так называемой функции активации (activation function). Функция активации ограничивает выходное значение нейрона предопределенным диапазоном, симулируя поведение оператора if.

Простейшей функцией активации является линейный выпрямитель (rectified linear unit, ReLU), что по сути является f32::max:

Другой популярной функцией активации является tanh - ее граф выглядит несколько иначе (похож на s), и она имеет другие свойства.

Функция активации влияет на входное и выходное значения. Например, tanh заставляет сеть работать с числами в диапазоне <-1.0, 1.0>, ReLU - в диапазоне <0.0, +inf>.

Как мы видим, когда наша взвешенная сумма со смещением меньше нуля, выходным значением нейрона будет 0.0. Это как раз то, что происходит в нашем случае:

max(-0.2, 0.0) = 0.0

Отлично, теперь разберемся с нижним левым нейроном:

# Взвешенная сумма:
0.8 * 1.0 = 0.8

# Смещение:
0.8 + 0.0 = 0.8

# Функция активации:
max(0.8, 0.0) = 0.8

Вычисление входного слоя завершено:

...что приводит нас к последнему нейрону:

# Взвешенная сумма:
(0.0 * 0.6) + (0.8 * 0.5) = 0.4

# Смещение:
0.4 + 0.2 = 0.6

# Функция активации:
max(0.6, 0.0) = 0.6

...и выводу всей сети:

0.6 * 1.0 = 0.6

Вуаля: для входного значения (0.5, 0.8) наша сеть отвечает 0.6 (в нашем случае это число ничего не значит).

Несмотря на то, что это одна из самых простых FFNN, при наличии соответствующих весов, она способна решить проблему XOR. Но управлять птицей она не может.

Более сложные FFNN, такие как эта:

...работают точно также: мы двигаемся слева направо, нейрон за нейроном, вычисляя выходные значений, пока не получим все числа из выходного слоя (на представленной диаграмме некоторые синапсы пересекаются, но это ничего не значит - это просто неудачное представление многомерных графов на плоском экране).

Вы можете задать вопрос: "Как узнать веса сети?". Ответ прост: в качестве весов используются произвольные значения!

Если вы привыкли к детерминированным алгоритмам (сортировка пузырьком), это может вас раздражать, но так работают сети, состоящие более чем из нескольких нейронов: мы скрещиваем пальцы, рандомизируем начальные веса и работаем с тем, что получили.

Обратите внимание, я сказал начальные веса - некоторые ненулевые веса. Существуют алгоритмы, позволяющие улучшить сеть (по сути, обучить ее).

Одним из самых популярных "обучающих" алгоритмов для FFNN является обратное распространение (backpropagation):

Мы показываем сети много (сотни тысяч) примеров в форме "для этого входного значения, ты должна возвращать это", и алгоритм медленно меняет веса сети до тех пор, пока не получит правильные ответы.

Или нет - сеть может застрять в локальном оптимуме и перестать учиться.

Обратное распространение - это пример обучения с учителем (supervised learning).

Обратное распространение - отличный инструмент, когда у нас имеется большой набор размеченных примеров (таких как фотографии или статистика), поэтому он нам не подходит: мы хотим, чтобы наши птицы учились всему самостоятельно.

Решение?

Генетические алгоритмы и магия больших чисел.

Генетический алгоритм: введение

С математической точки зрения наша основная проблема состоит в том, что у нас есть функция (представленная с помощью нейронной сети), которая определяется с помощью большого количества параметров:

Если каждый параметр будет представлен числом с плавающей точкой одинарной точности, сеть, состоящая всего из 3 нейронов и 5 синапсов, можно определить в таком количестве разных комбинаций...

(3.402 * 10^38) ^ (3 + 5) ~= 1.8 * 10^308

Сколько здесь чисел с плавающей точкой?

...что тепловая смерть Вселенной наступит быстрее, чем мы закончим их проверять - нам нужно быть умнее!

Все возможные наборы параметров называются пространством поиска (search space).

Поскольку перебор нашего пространства поиска в поисках единственного лучшего ответа не обсуждается, мы можем сосредоточиться на гораздо более простой задаче - поиске списка неоптимальных ответов.

И для этого нам нужно погрузиться глубже.

Генетический алгоритм: глубокое погружение

Это дикая морковь и ее одомашненная форма:

Эта одомашненная широко известная форма не появилась из ниоткуда, она является результатом сотен лет искусственного отбора по определенным критериям, таким как текстура или цвет корня.

Было бы здорово, если бы мы могли проделать тоже самое с нашими нейронными мозгами. Если мы создадим группу произвольных птиц и выборочно отберем тех, которые кажутся наиболее приспособленными... хм.

Оказывается, мы не первые, кому в голову пришла эта идея - существует целая отрасль информатики, называемая "эволюционными вычислениями", которая занимается решением проблем "точно так, как это делает природа".

Из всех эволюционных алгоритмов конкретный подкласс, который мы будем изучать, называется "генетическим алгоритмом".

Как и в случае с нейронными сетями, нет одного генетического алгоритма - существует множество разных алгоритмов. Поэтому, мы рассмотрим, как все работает в целом.

Генетический алгоритм начинается с популяции:

Популяция состоит из особей (individuals) (иногда называемых агентами (agents)):

Особь - это одно возможное решение определенной задачи (отсюда популяция - это набор возможных решений).

В нашем случае каждая особь будет моделировать мозг (или всю птицу, если угодно), но обычно это зависит от проблемы, которую вы решаете:

• если мы пытаемся эволюционировать антенну, особь будет одной антенной
• если мы пытаемся эволюционировать план запроса, особь будет одним планом запроса

Особь представляет некоторое решение, не обязательно лучшее.

Особь состоит из генов (совокупность генов особи называется геномом):

Геном представлен весами нейронной сети. Геном может быть списком чисел, графом или чем угодно, что способно моделировать решение задачи

Ген - это единичный параметр, который эволюционирует и настраивается генетическим алгоритмом.

В нашем случае каждый ген будет просто весом нейронной сети, но представление предметной области не всегда является настолько простым.

Например, если мы пытаемся помочь приятелю коммивояжеру, и основная проблема вообще не основана на нейронных сетях, одиночный ген может представлять собой кортеж координат (x, y), определяющий часть пути коммивояжера (в этом случае особь будет описывать весь его путь):

Теперь предположим, что у нас есть произвольная популяция из 50 птиц - мы передаем их генетическому алгоритму, что происходит?

Как и в случае с искусственным отбором, генетический алгоритм начинает с оценки каждой особи (каждого из возможных решений), чтобы определить, какие из них являются лучшими для текущей популяции.

С биологической точки зрения это эквивалентно прогулке по саду и проверке, какая морковь самая оранжевая и вкусная.

Оценка происходит с использованием так называемой функции приспособленности (fitness function), которая возвращает оценку приспособленности (fitness score), количественно определяющую, насколько хороша конкретная особь (то есть конкретное решение):

Пример фитнес-функции, которая количественно оценивает морковь по цвету и радиусу ее корня

Создание пригодной для использования функции приспособленности - одна из самых сложных задач, когда дело касается генетических алгоритмов, поскольку обычно существует множество показателей, по которым можно оценивать особь.

Даже наша воображаемая морковка имеет как минимум три показателя: цвет, радиус корня и вкус, и все их нужно свести в одно число.

К счастью, когда дело касается птиц, нам особо не из чего выбирать: "качество" птицы определяется количеством пищи, которую она съела в течение текущего поколения.

Птица, съевшая 30 единиц еды, лучше той, которая съела всего 20 - вот и все.

Отрицание функции приспособленности заставляет генетический алгоритм возвращать худшие решения вместо лучших - просто забавный трюк, который стоит запомнить на будущее.

Теперь пришло время для главного генетического алгоритма: воспроизводства (reproduction)!

В широком смысле воспроизводство - это процесс создания новой (в идеале, несколько улучшенной) популяции, на основе нынешней.

Это математический эквивалент выбора самой вкусной моркови и посадки ее семян.

Происходит следующее: генетический алгоритм произвольно выбирает двух особей (отдавая предпочтение тем, у которых более высокие показатели приспособленности) и использует их для создания двух новых особей (так называемого потомства (offspring)):

Потомство получается путем взятия геномов обоих родителей и проведения над ними скрещивания (crossover - кроссинговер) и мутации:

Скрещивание позволяет смешивать два разных генома для получения приблизительного промежуточного решения, а мутация позволяет обнаруживать новые решения, которых не было в исходной популяции.

Обе новые особи попадают в new population (новую популяцию), и процесс повторяется, пока не будет создана вся новая популяция. Затем текущая популяция отбрасывается, и все моделирование повторяется с этой новой (в идеале, улучшенной) популяцией.

Как видите, в этом процессе много случайностей: мы начинаем c произвольной популяции, рандомизируем распределение генов…​ ​это не может работать, не так ли?

Часть 2

В этой части мы заложим основы нашего проекта и реализуем простую FFNN (feedforward neural network - нейронная сеть прямого распространения), которая впоследствии станет мозгом. Мы также рассмотрим множество тонкостей и идиом, которые встречаются в коде Rust, включая тесты.

Настройка

Создаем новый проект:

mkdir shorelark
cd shorelark

Прежде всего, нам нужно определить, какую версию набора инструментов (toolchain) мы будем использовать - в противном случае, некоторые части кода могут работать не так, как ожидается.

По состоянию на март 2024 года последней стабильной версией Rust является 1.76, поэтому создаем файл rust-toolchain следующего содержания:

1.76.0

Теперь самое сложное - нам нужно определиться со структурой нашего проекта. Поскольку он будет состоять из множества независимых подмодулей (таких как нейронная сеть и генетический алгоритм), нам пригодится рабочая область (workspace):

# Cargo.toml
[workspace]
resolver = "2"

members = [
    "libs/*",
]

Это означает, что вместо обычного src/main.rs, мы создадим директорию libs и поместим туда наши библиотеки (крейты):

mkdir libs
cd libs
cargo new neural-network --name lib-neural-network --lib

Существует много подходов к организации рабочих пространств. Вместо того, чтобы хранить все в директории libs, можно хранить все в директории crates. Или можно создать две отдельные директории: одну для крейтов приложения, другую — для крейтов библиотек:

project
├─ Cargo.toml
├─ app
│  ├─ Cargo.toml
│  └─ src
│      └─ main.rs
└─ libs
   ├─ subcrate-a
   │  ├─ Cargo.toml
   │  └─ src
   │     └─ lib.rs
   └─ subcrate-b
      ├─ Cargo.toml
      └─ src
         └─ lib.rs

Разработка propagate()

Пора заняться делом.

Начнем сверху вниз со структуры, моделирующей сеть - она обеспечит точку входа в наш крейт. Редактируем lib.rs:

// libs/neural-network/src/lib.rs
#[derive(Debug)]
pub struct Network;

Самая важная операция нейронной сети - распространение (передача) чисел:

...поэтому:

#[derive(Debug)]
pub struct Network;

impl Network {
    pub fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> {
        todo!()
    }
}

Некоторые языки программирования позволяют оставлять разрабатываемые функции пустыми:

int get_berry_number() {
    // TODO решить парадокс
}

но эквивалентный код Rust не будет компилироваться:

fn berry_number() -> usize {
    // TODO решить парадокс
}

error[E0308]: mismatched types
 --> src/lib.rs
  |
1 | fn berry_number() -> usize {
  |    ------------      ^^^^^ expected `usize`, found `()`
  |    |
  |    implicitly returns `()` as its body has no tail or `return`
  |    expression

Это объясняется тем, что почти все в Rust является выражением:

// это выражение
let value = if condition {
    "computer says yass"
} else {
    "computer says no"
};

// и это выражение
let value = loop {
    break 123;
};

let value = {
    // пустой блок - это тоже выражение
};

...поэтому Rust видит эту функцию так:

fn berry_number() -> usize {
    return ();
}

() называется единичным значением (unit value) (или единичным типом (unit type), в зависимости от контекста).

Rust предоставляет два макроса, позволяющие пометить функцию как находящуюся в процессе разработки: todo!() и устаревший unimplemented!().

Оба макроса позволяют компилировать код и, если встречаются во время выполнения, приводят к безопасному сбою приложения:

thread 'main' panicked at 'not yet implemented'

Подобно океану, состоящему из капель, сеть состоит из слоев:

...поэтому:

#[derive(Debug)]
pub struct Network {
    layers: Vec<Layer>,
}

#[derive(Debug)]
struct Layer;

Слои состоят из нейронов:

...поэтому:

#[derive(Debug)]
struct Layer {
    neurons: Vec<Neuron>,
}

Наконец, нейроны содержат смещения (biases) и выходные (output) веса:

#[derive(Debug)]
struct Neuron {
    bias: f32,
    weights: Vec<f32>,
}

Взглянем на наш начальный проект целиком:

#[derive(Debug)]
pub struct Network {
    layers: Vec<Layer>,
}

impl Network {
    pub fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> {
        todo!()
    }
}

#[derive(Debug)]
struct Layer {
    neurons: Vec<Neuron>,
}

#[derive(Debug)]
struct Neuron {
    bias: f32,
    weights: Vec<f32>,
}

Отлично.

Вы могли заметить, что только два объекта являются общедоступными (pub): Network и Network:propagate().

Это связано с тем, что Layer и Neuron останутся деталями реализации, мы не будем делать их общедоступными.

Благодаря такому подходу мы сможем вносить изменения в нашу реализацию, не навязывая критических изменений другим крейтам (пользователям нашей библиотеки).

Например, настоящие нейронные сети обычно реализуются с помощью матриц - если мы решим переписать нашу сеть для использования матриц, это не будет критическим изменением: сигнатура Network:propagate() останется прежней, а поскольку пользователи не имеют доступа к Layer и Neuron, они не заметят их исчезновения.

Далее, поскольку числа необходимо передавать через каждый слой, в них нам также понадобится propagate():

impl Layer {
    fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> {
        todo!()
    }
}

Имея Layer::propagate(), мы можем вернуться и реализовать Network::propagate():

impl Network {
    pub fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> {
        let mut inputs = inputs;

        for layer in &self.layers {
            inputs = layer.propagate(inputs);
        }

        inputs
    }
}

Это вполне удовлетворительный и правильный фрагмент кода, но он не идиоматичен - мы можем сделать его лучше, более rustic!

Прежде всего, это называется перепривязкой (повторной привязкой, rebinding) (или затенением (shadowing)):

let mut inputs = inputs;

...и в этом нет необходимости, потому что мы можем переместить этот mut в параметр функции:

impl Network {
    pub fn propagate(&self, mut inputs: Vec<f32>) -> Vec<f32> {
        for layer in &self.layers {
            inputs = layer.propagate(inputs);
        }

        inputs
    }
}

Но не обяжет ли это вызывающую сторону передавать изменяемые (мутабельные) значения? Неа!

fn process(mut items: Vec<f32>) {
    // ...
}

fn main() {
    let items = vec![1.2, 3.4, 5.6];
    // ^ `mut` здесь не нужен

    process(items);
    //      ^ просто работает
}

Только что введенный нами mut находится в так называемой позиции привязки (binding position):

// иммут. - иммутабельный, мут. - мутабельный
fn foo_1(items: &[f32]) {
    //   ^^^^^  ------
    //  привязка  тип
    //  (иммут.) (иммут.)
}

fn foo_2(mut items: &[f32]) {
    //   ^^^^^^^^^  ------
    //    привязка   тип
    //     (мут.)  (иммут.)
}

fn foo_3(items: &mut [f32]) {
    //   ^^^^^  ----------
    //  привязка   тип
    //  (иммут.)  (мут.)
}

fn foo_4(mut items: &mut [f32]) {
    //   ^^^^^^^^^  ----------
    //    привязка    тип
    //     (мут.)    (мут.)
}

struct Person {
    name: String,
    eyeball_radius: usize,
}

fn decompose(Person { name, mut eyeball_radius }: Person) {
    //       ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^  ------
    //                     привязка                тип
    //         (частично иммут., частично мут.)  (иммут.)
}

...и привязки, в отличие от типов, являются локальными для функции:

fn foo(items: &mut Vec<usize>) {
    // Когда тип является мутабельным, мы можем модифицировать то,
    // на что указывает ссылка:
    items.push(1234);

    // Но если привязка остается иммутабельной, мы НЕ можем модифицировать
    // саму ссылку:
    items = some_another_vector;
    //    ^ error: cannot assign to immutable argument
}

fn bar(mut items: &Vec<usize>) {
    // С другой стороны, когда привязка является мутабельной, мы можем модифицировать
    // саму ссылку:
    items = some_another_vector;

    // Но если тип остается иммутабельным, мы не можем модифицировать то,
    // на что указывает ссылка:
    items.push(1234);
    //   ^^^^^ error: cannot borrow `*items` as mutable, as it is
    //         behind a `&` reference
}

Есть еще одна вещь, которую мы можем применить к нашему коду - этот шаблон известен как свертывание (folding):

for layer in &self.layers {
    inputs = layer.propagate(inputs);
}

...и стандартная библиотека Rust предоставляет для этого специальную функцию:

impl Network {
    pub fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> {
        self.layers
            .iter()
            .fold(inputs, |inputs, layer| layer.propagate(inputs))
    }
}

На вкус и цвет, как известно, товарища нет.

Вуаля - в конце концов, благодаря замыканию нам даже не нужен mut inputs - теперь наш код полностью соответствует Haskell (т.е. является функциональным по духу).

Перейдем к нейронам - один нейрон принимает много входных данных и возвращает одно выходное значение, поэтому:

#[derive(Debug)]
struct Neuron {
    bias: f32,
    weights: Vec<f32>,
}

impl Neuron {
    fn propagate(&self, inputs: Vec<f32>) -> f32 {
        todo!()
    }
}

Возвращаемся к реализации Layer::propagate():

#[derive(Debug)]
struct Layer {
    neurons: Vec<Neuron>,
}

impl Layer {
    fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> {
        let mut outputs = Vec::new();

        for neuron in &self.neurons {
            let output = neuron.propagate(inputs);
            outputs.push(output);
        }

        outputs
    }
}

Если мы попытаемся скомпилировать этот код, то получим первый сбой проверки заимствований:

error[E0382]: use of moved value: `inputs`
  --> src/lib.rs
   |
   |     fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> {
   |                         ------ move occurs because `inputs` has
   |                                type `Vec<f32>`, which does not
   |                                implement the `Copy` trait
  ...
   |             let output = neuron.propagate(inputs);
   |                                           ^^^^^^
   |                                value moved here, in previous
   |                                iteration of loop

Очевидно, что компилятор прав: после вызова neuron.propagate(inputs) мы теряем владение над inputs, поэтому не можем использовать их в последующих итерациях цикла.

К счастью, исправить это легко - достаточно сделать так, чтобы neuron::propagate() работал с заимствованными значениями:

impl Layer {
    fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> {
        /* ... */

        for neuron in &self.neurons {
            let output = neuron.propagate(&inputs);
            /* ... */
        }

        /* ... */
    }
}

/* ... */

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> f32 {
        /* ... */
    }
}

Вот как выглядит наш код на данный момент:

impl Layer {
    fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> {
        let mut outputs = Vec::new();

        for neuron in &self.neurons {
            let output = neuron.propagate(&inputs);
            outputs.push(output);
        }

        outputs
    }
}

...и, верите или нет, этот шаблон называется отображением (mapping), и стандартная библиотека также предоставляет для него специальный метод!

impl Layer {
    fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> {
        self.neurons
            .iter()
            .map(|neuron| neuron.propagate(&inputs))
            .collect()
    }
}

Остается завершить neuron::propagate() - как и прежде, начнем с сырой версии:

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> f32 {
        let mut output = 0.0;

        for i in 0..inputs.len() {
            output += inputs[i] * self.weights[i];
        }

        output += self.bias;

        if output > 0.0 {
            output
        } else {
            0.0
        }
    }
}

Этот фрагмент содержит две неидиоматичные конструкции и одну потенциальную ошибку - начнем с последней.

Поскольку мы перебираем self.weights, используя длину inputs, у нас есть три крайних случая:

1. Когда inputs.len() < self.weights.len().
2. Когда inputs.len() == self.weights.len().
3. Когда inputs.len() > self.weights.len().

Наш код основан на предположении, что пункт 2 всегда верен, но это предположение: мы нигде его не проверяем! Если мы по ошибке передадим меньше или больше входных данных, то получим либо неверный результат, либо сбой.

Существует как минимум два способа решить эту проблему:

1. Мы можем изменить Neuron::propagate() для возврата сообщения об ошибке:

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> Result<f32, String> {
        if inputs.len() != self.weights.len() {
            return Err(format!(
                "получено {} входных данных, ожидалось {}",
                inputs.len(),
                self.weights.len(),
            ));
        }

        /* ... */
    }
}

...или с помощью одного из моих любимых крейтов - thiserror:

pub type Result<T> = std::result::Result<T, Error>;

#[derive(Debug, Error)]
pub enum Error {
    #[error("получено {got} входных данных, ожидалось {expected}")]
    MismatchedInputSize {
        got: usize,
        expected: usize,
    },
}

/* ... */

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> Result<f32> {
        if inputs.len() != self.weights.len() {
            return Err(Error::MismatchedInputSize {
                got: inputs.len(),
                expected: self.weights.len(),
            });
        }

        /* ... */
    }
}

2. Мы можем использовать assert_eq!() / panic!():

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> f32 {
        assert_eq!(inputs.len(), self.weights.len());

        /* ... */
    }
}

В большинстве случаев первый вариант лучше, поскольку он позволяет вызывающей стороне поймать ошибку и легко ее обработать. Однако в нашем случае игра не стоит свеч, поскольку:

1. Если assert_eq() не сработает, значит, наша реализация, скорее всего, неверна, и пользователи ничего не смогут сделать со своей стороны, чтобы решить проблему.
2. Это игрушечный проект - не будем зря тратить время.

Поэтому:

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> f32 {
        assert_eq!(inputs.len(), self.weights.len());

        /* ... */
    }
}

Что касается идиом, это:

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> f32 {
        /* ... */

        if output > 0.0 {
            output
        } else {
            0.0
        }
    }
}

...является скрытым f32::max():

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> f32 {
        /* ... */

        output.max(0.0)
    }
}

А это:

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> f32 {
        /* ... */

        let mut output = 0.0;

        for i in 0..inputs.len() {
            output += inputs[i] * self.weights[i];
        }

        /* ... */
    }
}

...можно упростить сначала с помощью .zip():

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> f32 {
        /* ... */

        let mut output = 0.0;

        for (&input, &weight) in inputs.iter().zip(&self.weights) {
            output += input * weight;
        }

        /* ... */
    }
}

Операции индексации массива, такие как inputs[i], всегда выполняют так называемую проверку границ (bounds check) - это фрагмент кода, который гарантирует, что индекс находится в пределах массива, и паникует, когда он слишком велик:

fn main() {
    let numbers = vec![1];
    println!("{}", numbers[123]);
}

thread 'main' panicked at 'index out of bounds: the len is 1 but
the index is 123'

Когда вместо индексации мы используем комбинаторы, такие как .zip() или .map(), мы позволяем компилятору опустить эти проверки, что делает наш код не только более читаемым (на вкус и цвет...), но и более быстрым.

...затем с помощью .map() и .sum():

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> f32 {
        /* ... */

        let mut output = inputs
            .iter()
            .zip(&self.weights)
            .map(|(input, weight)| input * weight)
            .sum::<f32>();

        /* ... */
    }
}

Синтаксис ::<>, используемый на последней строке, называется турборыбой (turbofish). Он позволяет предоставлять явные общие (generic) аргументы, когда у компилятора возникают проблемы с их выводом.

Вуаля:

impl Neuron {
    fn propagate(&self, inputs: &[f32]) -> f32 {
        assert_eq!(inputs.len(), self.weights.len());

        let output = inputs
            .iter()
            .zip(&self.weights)
            .map(|(input, weight)| input * weight)
            .sum::<f32>();

        (self.bias + output).max(0.0)
    }
}

Это, несомненно, красиво, но работает ли это? Может ли наш код распознать кошку на изображении? Можем ли мы использовать его для прогнозирования будущих цен Dogecoin?

Разработка new()

До сих пор мы были настолько сосредоточены на алгоритме, что практически не думали о конструкторах, но как можно использовать сеть, которую невозможно создать?

Мы могли бы сделать так:

#[derive(Debug)]
pub struct Network {
    layers: Vec<Layer>,
}

impl Network {
    pub fn new(layers: Vec<Layer>) -> Self {
        Self { layers }
    }

    /* ... */
}

...но не будем, поскольку хотим оставить Layer и Neuron вне общедоступного интерфейса.

В прошлой статье мы много говорили о произвольных числах, поэтому я уверен, что рано или поздно нам понадобится что-то вроде этого:

impl Network {
    pub fn random() -> Self {
        todo!()
    }
}

Чтобы рандомизировать сеть, нам нужно знать количество ее слоев и количество нейронов в каждом слое - их можно описать одним вектором:

impl Network {
    pub fn random(neurons_per_layer: Vec<usize>) -> Self {
        todo!()
    }
}

...или более элегантным способом:

#[derive(Debug)]
pub struct LayerTopology {
    pub neurons: usize,
}

impl Network {
    pub fn random(layers: Vec<LayerTopology>) -> Self {
        todo!()
    }

    /* ... */
}

// Заметьте, как создание отдельного типа позволило нам переименовать аргумент просто в `layers`.
//
// Изначально аргумент назывался `neurons_per_layer`, поскольку `Vec<usize>`
// не предоставлял достаточно информации о том, что представляет собой этот `usize`.
// Использование отдельного типа делает это очевидным.

Теперь, если внимательно посмотреть на слой нейронной сети:

...можно заметить, что на самом деле он определяется двумя числами: размерами входных и выходных данных. Означает ли это, что наша структура LayerTopology с одним полем неверна? Наоборот!

Мы использовали знания в предметной области.

В FFNN все слои соединены последовательно слева направо:

Поскольку выходные данные слоя A являются входными данными слоя B, если мы сделаем так:

#[derive(Debug)]
pub struct LayerTopology {
    pub input_neurons: usize,
    pub output_neurons: usize,
}

...тогда мы не только сделаем наш интерфейс громоздким, но, что еще хуже, нам потребуется дополнительная проверка, гарантирующая, что соблюдаются условия layer[0].output_neurons == layer[1].input_neurons и т.д. - полная бессмыслица!

Принимая во внимание тот простой факт, что последовательные слои должны иметь совпадающие входы и выходы, мы можем упростить код еще до его написания.

Наивная реализация выглядит так:

impl Network {
    pub fn random(layers: Vec<LayerTopology>) -> Self {
        let mut built_layers = Vec::new();

        for i in 0..(layers.len() - 1) {
            let input_size = layers[i].neurons;
            let output_size = layers[i + 1].neurons;

            built_layers.push(Layer::random(
                input_size,
                output_size,
            ));
        }

        Self { layers: built_layers }
    }
}

...давайте ее "растифицируем" - угадайте, что произойдет, если мы вызовем Network::random(vec![])?

impl Network {
    pub fn random(layers: Vec<LayerTopology>) -> Self {
        // Сеть с одним слоем технически возможна, но бессмысленна:
        assert!(layers.len() > 1);

        /* ... */
    }
}

Так лучше.

Что касается цикла for, то итерация по соседним элементам - это еще один шаблон, предоставляемый стандартной библиотекой через метод windows():

impl Network {
    pub fn random(layers: Vec<LayerTopology>) -> Self {
        /* ... */

        for adjacent_layers in layers.windows(2) {
            let input_size = adjacent_layers[0].neurons;
            let output_size = adjacent_layers[1].neurons;

            /* ... */
        }

        /* ... */
    }
}

Если вы знаете о деструктуризации, то можете попробовать переписать этот цикл следующим образом:

for [fst, snd] in layers.windows(2) {
    built_layers.push(Layer::random(fst.neurons, snd.neurons));
}

...но, к сожалению, компьютер говорит "Нет":

error[E0005]: refutable pattern in `for` loop binding: `&[]`,
              `&[_]` and `&[_, _, _, ..]` not covered
 --> src/lib.rs
  |
  |     for [fst, snd] in layers.windows(2) {
  |         ^^^^^^^^^^ patterns `&[]`, `&[_]` and `&[_, _, _, ..]`
  |                    not covered
  |
  = note: the matched value is of type `&[LayerTopology]`

Компилятор не понимает, что windows(2) возвращает массив, состоящий ровно из двух элементов, ему известно лишь, что windows() может возвращать массивы произвольных размеров, которые не обязательно соответствуют нашему шаблону (этот шаблон называется опровержимым (refutable), потому что он не совпадает со всеми возможными случаями; трюк с деструктуризацией можно провернуть только с помощью неопровержимого (irrefutable) шаблона).

Ночной Rust, содержащий константные дженерики (const generics) предлагает решение - .array_windows():

#![feature(array_windows)]

for [fst, snd] in layers.array_windows() {
    built_layers.push(Layer::random(fst.neurons, snd.neurons));
}

...однако для простоты мы не будем использовать константные дженерики и продолжим работать со стабильной функцией.

В этом случае переход на итераторы для меня является очевидным:

impl Network {
    pub fn random(layers: Vec<LayerTopology>) -> Self {
        let layers = layers
            .windows(2)
            .map(|layers| Layer::random(layers[0].neurons, layers[1].neurons))
            .collect();

        Self { layers }
    }
}

И последний штрих: если это не делает код неудобным, рекомендуется принимать заимствованные значения вместо собственных:

impl Network {
    pub fn random(layers: &[LayerTopology]) -> Self {
        /* ... */
    }
}

Чаще всего принятие заимствованных значений не сильно меняет логику функции, но делает ее более универсальной - с заимствованным массивом теперь можно делать следующее:

let network = Network::random(&[
    LayerTopology { neurons: 8 },
    LayerTopology { neurons: 15 },
    LayerTopology { neurons: 2 },
]);

...и:

let layers = vec![
    LayerTopology { neurons: 8 },
    LayerTopology { neurons: 15 },
    LayerTopology { neurons: 2 },
];

let network_a = Network::random(&layers);
let network_b = Network::random(&layers);
//                              ^ нет необходимости в `.clone()`

Что дальше, что дальше... проверяем заметки... а, Layer::random()!

impl Layer {
    fn random(input_size: usize, output_size: usize) -> Self {
        let mut neurons = Vec::new();

        for _ in 0..output_size {
            neurons.push(Neuron::random(input_size));
        }

        Self { neurons }
    }

    /* ... */
}

...или:

impl Layer {
    fn random(input_size: usize, output_size: usize) -> Self {
        let neurons = (0..output_size)
            .map(|_| Neuron::random(input_size))
            .collect();

        Self { neurons }
    }
}

|_| называется toilet closure (гардеробным замыканием?) - это функция, принимающая аргумент, который ей не важен/нужен.

Мы могли бы написать:

.map(|output_neuron_id| Neuron::random(input))

...но поскольку нам не нужно читать этот output_neuron_id, более идиоматичным будет назвать аргумент _ (или хотя бы _output_neuron_id) для индикации факта неиспользуемости.

Сам _ называется заменителем (placeholder) и может использоваться в разных контекстах:

// Как привязка:
fn ignore_some_arguments(_: usize, b: usize, _: usize) {
    //                   ^                   ^
}

// ...но не как название:
fn _() {
// ^ error: expected identifier, found reserved identifier `_`
}

// Как тип:
fn load_files(paths: &[&Path]) -> Vec<String> {
    paths
        .iter()
        .map(std::fs::read_to_string)
        .collect::<Result<_, _>>()
    //                    ^  ^
        .unwrap()
}

// ...но только внутри выражений:
fn what_am_i(foo: _) {
    //            ^ error: the type placeholder `_` is not allowed
    //              within types on item signatures
}

Наконец, последний фрагмент нашей цепочки - Neuron::random():

impl Neuron {
    fn random(input_size: usize) -> Self {
        let bias = todo!();

        let weights = (0..input_size)
            .map(|_| todo!())
            .collect();

        Self { bias, weights }
    }

    /* ... */
}

В отличие от C++ или Python, стандартная библиотека Rust не предоставляет генератора псевдослучайных чисел (далее также - ГПСЧ). Что это означает? Это означает, что пришло время для crates.io!

Когда дело доходит до ГПСЧ, rand фактически является стандартом. Это чрезвычайно универсальный крейт, который позволяет генерировать не только псевдослучайные числа, но и другие типы, такие как строки.

Добавляем его в Cargo.toml:

# ...

[dependencies]
rand = "0.8"

...и затем:

use rand::Rng;

/* ... */

impl Neuron {
    fn random(input_size: usize) -> Self {
        let mut rng = rand::thread_rng();
        let bias = rng.gen_range(-1.0..=1.0);

        let weights = (0..input_size)
            .map(|_| rng.gen_range(-1.0..=1.0))
            .collect();

        Self { bias, weights }
    }
}

0..3 - это полуоткрытый интервал, который совпадает с 0, 1 и 2. 0..=3 - это закрытый интервал, который также включает 3.

Конечно, rng.gen_range(-1.0..=1.0) довольно точно предсказывает цены Dogecoin, но существует ли способ убедиться, что наша сеть работает, как ожидается?

Тестирование

Чистая функция - это функция, которая при одних и тех же аргументах всегда возвращает одно и то же значение. Например, это чистая функция:

pub fn add(x: usize, y: usize) -> usize {
    x + y
}

...а это нет:

pub fn read(path: impl AsRef<Path>) -> String {
    std::fs::read_to_string(path).unwrap()
}

add(1, 2) всегда возвращает 3, в то время как read("file.txt") будет возвращать разные строки в зависимости от того, что содержит файл file.txt в данный момент.

Чистые функции хороши тем, что их можно тестировать изолированно:

// Этот тест всегда проходит
// (он является *детерминированным*)
#[test]
fn test_add() {
    assert_eq!(add(1, 2), 3);
}

// Этот тест может пройти, а может провалиться, предугадать невозможно
// (он является *недетерминированным*)
#[test]
fn test_read() {
    assert_eq!(
        std::fs::read_to_string("serials-to-watch.txt"),
        "killing eve",
    );
}

К сожалению, генерация чисел в Neuron::random() делает эту функцию нечистой, что легко доказать:

#[test]
fn random_is_pure() {
    let neuron_a = Neuron::random(4);
    let neuron_b = Neuron::random(4);

    // Если бы `Neuron::random()` была чистой, оба нейрона всегда были бы одинаковыми:
    assert_eq!(neuron_a, neuron_b);
}

Тестировать нечистые функции сложно, потому что мы мало что можем утверждать достоверно:

/* ... */

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn random() {
        let neuron = Neuron::random(4);

        assert!(/* что? */);
    }
}

Мы можем попробовать:

#[test]
fn test() {
    let neuron = Neuron::random(4);

    assert_eq!(neuron.weights.len(), 4);
}

...но это бесполезный тест, он ничего не доказывает.

С другой стороны, превращать Neuron::random() в чистую функцию кажется... нелепым? Какой смысл в рандомизации, если результат всегда будет одинаковым?

Обычно я примиряю оба мира, рассматривая источник нечистоты. В данном случае это:

impl Neuron {
    fn random(input_size: usize) -> Self {
        let mut rng = rand::thread_rng(); // упс

        /* ... */
    }
}

Что если вместо вызова thread_rng(), мы будем принимать параметр с рандомизатором?

use rand::{Rng, RngCore};

/* ... */

impl Network {
    pub fn random(rng: &mut dyn RngCore, layers: &[LayerTopology]) -> Self {
        let layers = layers
            .windows(2)
            .map(|layers| Layer::random(rng, layers[0].neurons, layers[1].neurons))
            .collect();

        /* ... */
    }

    /* ... */
}

/* ... */

impl Layer {
    fn random(rng: &mut dyn RngCore, input_size: usize, output_size: usize) -> Self {
        let neurons = (0..output_size)
            .map(|_| Neuron::random(rng, input_size))
            .collect();

        /* ... */
    }

    /* ... */
}

/* ... */

impl Neuron {
    fn random(rng: &mut dyn RngCore, input_size: usize) -> Self {
        /* ... */
    }

    /* ... */
}

...тогда мы сможем использовать в наших тестах фиктивный, предсказуемый ГПСЧ, в то время как пользователи смогут передавать настоящий ГПСЧ по своему выбору.

Вы можете использовать аналогичный подход для проверки вывода приложения, если вместо:

fn do_something() {
    println!("Делаем что-нибудь...");
    println!("...сделано!");
}

...мы сделаем:

fn do_something(stdout: &mut dyn Write) {
    writeln!(stdout, "Делаем что-нибудь...").unwrap();
    writeln!(stdout, "...сделано!").unwrap();
}

...тогда мы сможем легко тестировать вывод:

#[test]
fn ensure_something_happens() {
    let mut stdout = String::new();
    do_something(&mut stdout);

    assert_eq!(stdout, "Делаем что-нибудь...\n...сделано!\n");
}

Я делал это раньше, и это оказалось очень удобным.

Технически ни do_something(), ни random() не являются чистыми функциями, поскольку им не хватает свойства, называемого ссылочной прозрачностью (referential transparency) - хотя всегда есть:

fn do_something<W: Write>(stdout: W) -> W {
    /* ... */
}

Поскольку крейт rand не предоставляет предсказуемого (фиктивного) ГПСЧ, нам придется использовать другой крейт — мне нравится rand_chacha (легко запомнить, вероятно, вы уже запомнили):

# ...

[dependencies]
rand = "0.8"

[dev-dependencies]
rand_chacha = "0.3"

...что позволяет нам сделать следующее:

#[cfg(test)]
mod tests {
    use super::*;
    use rand::SeedableRng;
    use rand_chacha::ChaCha8Rng;

    #[test]
    fn random() {
        // Поскольку мы всегда используем одинаковый заполнитель (seed), наш `rng`
        // будет всегда возвращать одинаковый набор значений
        let mut rng = ChaCha8Rng::from_seed(Default::default());
        let neuron = Neuron::random(&mut rng, 4);

        assert_eq!(neuron.bias, /* ... */);
        assert_eq!(neuron.weights, &[/* ... */]);
    }
}

Мы пока не знаем, какие числа будут возвращены, но это легко выяснить - мы просто начнем с нулей, а затем скопируем и вставим числа из результатов теста:

#[test]
fn random() {
    /* ... */

    assert_eq!(neuron.bias, 0.0);
    assert_eq!(neuron.weights, &[0.0, 0.0, 0.0, 0.0]);
}

Первый cargo test дает нам:

thread '...' panicked at 'assertion failed: `(left == right)`
  left: `-0.6255188`,
 right: `0.0`

...поэтому:

#[test]
fn random() {
    /* ... */

    assert_eq!(neuron.bias, -0.6255188);

    /* ... */
}

Второй cargo test дает:

thread '...' panicked at 'assertion failed: `(left == right)`
  left: `[0.67383957, 0.8181262, 0.26284897, 0.5238807]`,
 right: `[0.0, 0.0, 0.0, 0.0]`', src/lib.rs:29:5

...поэтому:

#[test]
fn random() {
    /* ... */

    assert_eq!(
        neuron.weights,
        &[0.67383957, 0.8181262, 0.26284897, 0.5238807]
    );
}

Обратите внимание, что числа разные, и это нормально - они могут быть разными, пока каждый cargo test работает с одним и тем же набором чисел (и это так, потому что мы использовали ГПСЧ с постоянным заполнителем).

Прежде чем двигаться дальше, нам нужно затронуть еще одну тему: неточность чисел с плавающей точкой (запятой).

Тип, который мы используем, f32, представляет собой 32-битное число с плавающей точкой, которое может представлять значения от ~1,2*10^-38 до ~3,4*10^38. Увы, он может представлять не все эти числа, а только некоторые.

Например, с помощью f32 мы не можем закодировать ровно 0.15:

fn main() {
    println!("{:.10}", 0.15f32);
    // 0.1500000060
}

...или 0.45:

fn main() {
   println!("{:.10}", 0.45f32);
   // 0.4499999881
}

Обычно это не имеет значения, потому что числа с плавающей точкой проектировались не для точности, а только для скорости, но иногда это похоже на кирпич, падающий с неба:

#[test]
fn test() {
    assert_eq!(0.45f32, 0.15 + 0.15 + 0.15);
}

thread 'test' panicked at 'assertion failed: `(left == right)`
  left: `0.45`,
 right: `0.45000002`'

Если вы не читали о числах с плавающей точкой, советую взглянуть на эту статью.

Итак, если мы не можем сравнивать числа точно, то как их сравнивать? Приблизительно!

#[test]
fn test() {
    let actual: f32 = 0.1 + 0.2;
    let expected = 0.3;

    assert!((actual - expected).abs() < f32::EPSILON);
}

Это стандартный способ сравнения чисел с плавающей точкой во всех языках программирования, реализующих IEEE 754 (по сути, во всех языках программирования) - вместо того, чтобы искать точный результат, мы сравниваем оба числа с отступом погрешности (margin of error) (также называемым допуском (tolerance)).

Поскольку сравнивать числа таким способом неудобно, это можно делать с помощью макроса:

macro_rules! assert_almost_eq {
    ($left:expr, $right:expr) => {
        let left: f32 = $left;
        let right: f32 = $right;

        assert!((left - right).abs() < f32::EPSILON);
    }
}

#[test]
fn test() {
    assert_almost_eq!(0.45f32, 0.15 + 0.15 + 0.15);
}

...или с помощью крейта, такого как approx:

#[test]
fn test() {
    approx::assert_relative_eq!(0.45f32, 0.15 + 0.15 + 0.15);
}

Мне нравится approx, добавляем его в Cargo.toml:

# ...

[dev-dependencies]
approx = "0.4"
rand_chacha = "0.3"

...и обновляем тесты:

use super::*;
use approx::assert_relative_eq;
use rand::SeedableRng;
use rand_chacha::ChaCha8Rng;

#[test]
fn random() {
    let mut rng = ChaCha8Rng::from_seed(Default::default());
    let neuron = Neuron::random(&mut rng, 4);

    assert_relative_eq!(neuron.bias, -0.6255188);

    assert_relative_eq!(
        neuron.weights.as_slice(),
        [0.67383957, 0.8181262, 0.26284897, 0.5238807].as_ref()
    );
}

После того, что мы узнали, написать тест для Neuron::propagate() не составляет труда:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn random() {
        /* ... */
    }

    #[test]
    fn propagate() {
        todo!()
    }
}

Вероятно, вы слышали, что тесты следует именовать, исходя из их предварительных условий и ожиданий.

Обычно это так - если бы мы разрабатывали магазин, было бы полезно структурировать тесты следующим образом:

#[cfg(test)]
mod tests {
    use super::*;

    mod cart {
        use super::*;

        mod when_user_adds_a_flower_to_their_cart {
            use super::*;

            #[test]
            fn user_can_see_this_flower_in_their_cart() {
                /* ... */
            }

            #[test]
            fn user_can_remove_this_flower_from_their_cart() {
                /* ... */
            }

            mod and_submits_order {
                /* ... */
            }

            mod and_abandons_cart {
                /* ... */
            }
        }
    }
}

Проблема в том, что наш Neuron не является типичным "бизнес-кодом", и многие "шаблоны бизнес-кода" не работают с математическим кодом. Если нам потребуется учитывать некоторые крайние случаи, скажем:

fn propagate(/* ... */) {
    if /* ... */ {
        do_foo()
    } else {
        do_bar()
    }
}

...тогда имеет смысл создать два отдельных теста:

#[cfg(test)]
mod tests {
    use super::*;

    mod propagate {
        use super::*;

        mod given_neuron_with_foo {
            use super::*;

            #[test]
            fn fooifies_it() {
                /* ... */
            }
        }

        mod given_neuron_thats_bar {
            use super::*;

            #[test]
            fn bars_it() {
                /* ... */
            }
        }
    }
}

...но в нашем случае лучше использовать простые fn random() и fn propagate().

Как убедиться в том, что propagate() работает правильно? Вычислить ожидаемый результат вручную:

#[test]
fn propagate() {
    let neuron = Neuron {
        bias: 0.5,
        weights: vec![-0.3, 0.8],
    };

    // Проверяем работу `.max()` (нашего ReLU):
    assert_relative_eq!(
        neuron.propagate(&[-10.0, -10.0]),
        0.0,
    );

    // `0.5` и `1.0` выбраны произвольно:
    assert_relative_eq!(
        neuron.propagate(&[0.5, 1.0]),
        (-0.3 * 0.5) + (0.8 * 1.0) + 0.5,
    );

    // Мы могли бы сразу написать `1.15`, но полная формула
    // делает наши намерения более ясными
}

Попробуйте самостоятельно реализовать тесты для Layer и Network.

Заключительные мысли

Что именно мы создали?

Может показаться, что реализованное нами не имеет ничего общего с обучением или моделированием:

• Что насчет глаз?
• Где код, отвечающий за движение?
• Как создать этот зеленоватый терминал в стиле Fallout?

...но это только потому, что сама нейронная сеть, хотя и является относительно сложной частью нашей кодовой базы, сама по себе почти ничего не делает - не волнуйтесь, в конце концов, все встанет на свои места.

А пока не стесняйтесь знакомиться с исходным кодом.

Почему наш код такой объемный?

При поиске "нейронная сеть на Python с нуля", мы находим множество статей, в которых FFNN реализуется с помощью нескольких строк кода Python - по сравнению с ними наш код кажется раздутым, почему так?

Потому что это позволяет многому научиться! Мы могли бы закодировать нашу сеть в 1/10 от ее текущего размера, используя nalgebra, мы могли бы использовать один из уже существующих крейтов, но нам важен не только пункт назначения, но и само путешествие.

Что дальше?

На данный момент у нас есть простая FFNN - в следующем разделе мы реализуем генетический алгоритм и подключим его к нашей нейронной сети.

Часть 3

В предыдущей части мы реализовали простую FFNN, которая может передавать числа через рандомизированные слои - это первый шаг на пути создания мозга.

Однако рандомизация - это далеко не все. По большей части эволюция заключается во внесении небольших, постепенных изменений, чтобы система со временем становилась лучше, чтобы наш мозг начал накапливать знания и функционировать так, как ожидается.

Но как мы можем обучить группу чисел с плавающей точкой (запятой, если угодно)?

Проект

Скоро мы узнаем, как работает генетический алгоритм, реализовав его на Rust. Мы подробно рассмотрим, как селекция, скрещивание и мутация вместе позволяют компьютеру находить сложные решения, казалось бы, из воздуха.

Мы постараемся не жестко кодировать конкретный алгоритм выбора или скрещивания, а использовать типажи для создания библиотеки, которую при желании даже можно будет опубликовать на crates.io!

Как и в предыдущей части, сегодня мы рассмотрим различные тонкости синтаксиса Rust, уделяя особое внимание терминологии.

Надеюсь, к концу этой статьи вы сможете сказать: я могу реализовать все это самостоятельно!

Введение

Для начала вспомним, как работает генетический алгоритм, и в чем смысл нашей затеи.

У нас есть объект - нейронная сеть, которая определяется множеством параметров. Их так много, что даже для самых маленьких сетей мы не сможем перебрать все их комбинации за всю нашу жизнь.

Все возможные параметры называются пространством поиска (search space); эрудит сказал бы, что пространство поиска нашей проблемы огромно, и после этого просто убежал бы.

Что мы можем сделать, так это попробовать подражать природе: если мы начнем с группы произвольных неоптимальных решений, мы можем попытаться улучшить их, чтобы со временем получить лучшие решения.

Одним из методов, позволяющих моделировать всю эту эволюционную технику, является генетический алгоритм - он начинается с группы произвольных кандидатов-решений (популяции), которые затем улучшаются с помощью мутаций и скрещиваний, используя функцию приспособленности для оценки найденных решений (особей):

Обзор генетического алгоритма; сверху по часовой стрелке: 1) оцениваем текущие решения с помощью функции приспособленности, 2) выполняем скрещивание и мутацию, 3) повторяем процесс с новой улучшенной популяцией.

Поскольку генетический алгоритм предполагает работу с произвольными числами, он является примером вероятностного метода.

Вероятностные алгоритмы жертвуют точностью ради производительности - они не всегда возвращают лучшие ответы, но обычно дают довольно хорошие результаты и делают это довольно дешево.

Производители овощей не хотят, чтобы вы знали об этом, но существует простая процедура, позволяющая стать морковным магнатом, основанная на генетическом алгоритме:

10  идем в сад
20  сеем несколько произвольных морковок
30  ждем, когда они вырастут
40  берем семена лучших морковок и сеем их
50  возвращаемся к 30

в этом случае:
- популяция = морковки
- особь = морковка
- мутация & скрещивание = происходят автоматически (бесплатный труд!)
- фитнес-функция = ваши глаза & мозг

К этому моменту большинство этих слов должны быть вам знакомы - мы уже рассматривали основы эволюционных вычислений в первой статье. К концу этой статьи вы получите ответы на такие вопросы, как:

• Как мы отбираем особей? Должна существовать тысяча способов делать это! (это правда)
• Как мы представляем их геномы? Должна существовать тысяча способов делать это! (это правда)
• Как реализовать это на Rust? Ты обещал, что код будет работать в браузере! (будет)

Разработка: схема

Начнем с создания второго крейта в нашем рабочем пространстве:

cd shorelark/libs
cargo new genetic-algorithm --name lib-genetic-algorithm --lib

Редактируем lib.rs:

pub struct GeneticAlgorithm;

Наш генетический алгоритм будет предоставлять только одну функцию - иногда ее называют iterate, иногда - step или process. Я решил быть оригинальным:

impl GeneticAlgorithm {
    pub fn evolve(&self) {
        todo!()
    }
}

Что мы эволюционируем? Популяцию, конечно!

impl GeneticAlgorithm {
    pub fn evolve(&self, population: &[???]) -> Vec<???> {
        todo!()
    }
}

Наша реальная проблема будет зависеть от нейронной сети, но поскольку мы хотим, чтобы эта библиотека была универсальной, мы не можем жестко закодировать NeuralNetwork в качестве принимаемого параметра - вместо этого мы можем указать параметр типа:

impl GeneticAlgorithm {
    pub fn evolve<I>(&self, population: &[I]) -> Vec<I> {
        todo!()
    }
}

I означает особь (individual):

// видимость  дженерики   _ параметры функции
// |          _|     ____|  (или просто "параметры")
// |         |      |
// v-v       v-----vv----------v
   pub fn foo<'a, T>(bar: &'a T) { /* ... */ }
//            ^^  ^  ^--------^
//            |   |  |
//            |   |  параметр функции
//            |   |  (или просто "параметр")
//            |   параметр типа
//            параметр времени жизни

Это читается так:

"Общедоступная функция foo является общей по времени жизни a и типу T, и принимает один параметр bar, который является ссылкой на T".

Это определение функции. В месте вызова функции передаваемые ей значения называются аргументами:

// v-----------------------v место вызова
   foo::<'static, f32>(&1.0);
//       ^-----^  ^-^  ^--^
//       |        |    |
//       |        |    аргумент функции
//       |        |    (или просто "аргумент")
//       |        аргумент типа
//       аргумент времени жизни

Не будем забывать о предварительных условиях:

impl GeneticAlgorithm {
    pub fn evolve<I>(&self, population: &[I]) -> Vec<I> {
        assert!(!population.is_empty());

        /* ... */
    }
}

Схема алгоритма:

impl GeneticAlgorithm {
    pub fn evolve<I>(&self, population: &[I]) -> Vec<I> {
        /* ... */

        (0..population.len())
            .map(|_| {
                // TODO отбор
                // TODO скрещивание
                // TODO мутация
                todo!()
            })
            .collect()
    }
}

Разработка: отбор

На этом этапе внутри цикла нам нужно выбрать двух особей - они станут родителями и "создадут" для нас цифровое потомство.

Выбор особей называется этапом отбора генетического алгоритма и должен удовлетворять следующим двум свойствам:

• каждая особь должна иметь ненулевой шанс быть выбранной
• особи с более высоким показателем приспособленности в среднем должны выбираться чаще, чем особи с более низким показателем приспособленности

Начнем с того, что подумаем, как мы хотим, чтобы пользователи предоставляли свою фитнес-функцию - как бы тривиально это ни звучало, здесь существует как минимум два взаимоисключающих подхода:

1. Фитнес-функция как параметр особи:

impl GeneticAlgorithm {
    pub fn evolve<I>(
        &self,
        population: &[I],
        evaluate_fitness: &dyn Fn(&I) -> f32,
    ) -> Vec<I> {
        /* ... */
    }
}

2. Показатель приспособленности как свойство особи:

pub trait Individual {
    fn fitness(&self) -> f32;
}

impl GeneticAlgorithm {
    pub fn evolve<I>(&self, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */
    }
}

Первый подход:

• ✅ позволяет предоставить множество различных фитнес-функций для одного типа особей, что может кому-то пригодиться (но не нам)
• ❌ требует указания фитнес-функции для каждого вызова .evolve(), что немного неудобно

Второй подход:

• ✅ позволяет инкапсулировать все индивидуально-ориентированные атрибуты в один типаж, облегчая понимание того, что пользователи должны предоставить
• ❌ указание различных фитнес-функций возможно, но делать это немного сложнее

Моя интуиция голосует 213:7 за использование типажа (он нам в любом случае понадобится, как вы увидите позже).

Что касается метода отбора, мы будем использовать алгоритм, который называется пропорциональным отбором по приспособленности (fitness proportionate selection) (также известный как выбор колеса рулетки (roulette wheel selection)), потому что его легко понять - представим, что у нас есть три особи:

Особь	Показатель приспособленности	Показатель приспособленности в %
A	3	3 / (1 + 2 + 3) = 3 / 6 = 50%
B	2	2 / (1 + 2 + 3) = 2 / 6 = 33%
C	1	1 / (1 + 2 + 3) = 1 / 6 = 16%

Если мы поместим их на колесо рулетки (или, если угодно, на круговую диаграмму), где каждая особь займет часть колеса, равную доле его показателя приспособленности ко всей популяции:

...тогда рандомизация особи будет сводиться к "вращению" колеса с произвольной силой и оценке того, что получилось:

На практике отбор, пропорциональный приспособленности, является, скорее, антипаттерном, потому что позволяет лучшим особям доминировать в симуляции.

Предположим, наш генетический алгоритм находит решение, которое намного лучше остальных:

...в этом случае отбор, пропорциональный приспособленности, с радостью будет выбирать это зеленое решение в 99% случаев, превращая остальных особей в армию скопированных зеленых клонов.

Вы можете задаться вопросом:

"Но разве наша цель состоит не в нахождении лучшего решения?"

Да, но важно помнить, что решения, найденные с помощью генетического алгоритма, всегда являются лучшими на сегодняшний день: если мы отбросим, казалось бы, бесперспективного кандидата слишком рано, то никогда не узнаем, не сделает ли настройка какого-либо параметра его лучше лучшего (простите за тавтологию) решения в долгосрочной перспективе.

Другими словами, чем больше у нас разных особей, тем больше шансов, что одна из них окажется вундеркиндом по игре на тромбоне.

Для простоты мы продолжим использовать выбор колеса рулетки, но отмечу, что выбор ранга (rank selection) - это пример алгоритма, который не демонстрирует доминирующего поведения лучших особей и будет работать с нашими птичками!

Вместо того, чтобы жестко кодировать нашу библиотеку для использования выбора колеса рулетки, создадим типаж. Это позволит пользователям предоставлять любой алгоритм, который им нравится:

pub trait SelectionMethod {
    fn select(&self);
}

Метод отбора должен иметь доступ ко всей популяции:

pub trait SelectionMethod {
    fn select<I>(&self, population: &[I]) -> &I
    where
        I: Individual;
}

...и, для ясности, укажем время жизни:

pub trait SelectionMethod {
    fn select<'a, I>(&self, population: &'a [I]) -> &'a I
    where
        I: Individual;
}

Нам потребуются произвольные числа, так что:

# ...

[dependencies]
rand = "0.8"

[dev-dependencies]
rand_chacha = "0.3"

Каждый крейт в рабочем пространстве имеет собственный набор зависимостей, поэтому rand, указанный в libs/neural-network/Cargo.toml, не доступен другим крейтам рабочего пространства.

Указываем ГПСЧ (генератор псевдослучайных чисел) как параметр:

use rand::RngCore;

/* ... */

pub trait SelectionMethod {
    fn select<'a, I>(&self, rng: &mut dyn RngCore, population: &'a [I]) -> &'a I
    where
        I: Individual;
}

Какая чудесная сигнатура, не правда ли?

Почему бы нам не пойти дальше и не сделать select() универсальным также для ГПСЧ?

pub trait SelectionMethod {
    fn select<'a, R, I>(
       &self,
       rng: &mut R,
       population: &'a [I],
    ) -> &'a I
    where
        R: RngCore,
        I: Individual;
}

Для начала разберемся в терминологии:

1. dyn Trait, &dyn Trait и &mut dyn Trait подразумевают динамическую диспетчеризацию (dynamic dispatch).
2. T, &T и &mut T подразумевают статическую диспетчеризацию (static dispatch).

Диспетчеризация - это способ, которым компилятор отвечает на вопрос "куда именно нам следует перейти?" для универсальных типов:

fn foo() {
   bar();
   // ^ компиляция этого вызова не составляет труда, поскольку мы всегда переходим в `bar`
}

fn bar() {
   println!("yas queen");
}

fn method(obj: &dyn SomeTrait) {
    obj.method();
    // ^ компиляция этого вызова сложнее, поскольку
    //   каждая реализация `SomeTrait` предоставляет
    //   собственную `fn method(&self) { ... }`
}

В качестве примера рассмотрим такой типаж с двумя реализациями:

trait Animal {
    fn kind(&self) -> &'static str;
}

// --

struct Chinchilla;

impl Animal for Chinchilla {
    fn kind(&self) -> &'static str {
        "chinchilla"
    }
}

// --

struct Viscacha;

impl Animal for Viscacha {
    fn kind(&self) -> &'static str {
        "viscacha"
    }
}

Если мы захотим создать функцию, которая печатает вид любого животного, мы можем сделать это двумя способами:

// С помощью статической диспетчеризации (статический полиморфизм):
fn print_kind_static<A>(animal: &A)
where
    A: Animal,
{
    println!("{}", animal.kind());
}

// С помощью динамической диспетчеризации (динамический полиморфизм, полиморфизм времени выполнения):
fn print_kind_dynamic(animal: &dyn Animal) {
    println!("{}", animal.kind());
}

fn main() {
    print_kind_static(&Chinchilla);
    print_kind_static(&Viscacha);

    print_kind_dynamic(&Chinchilla);
    print_kind_dynamic(&Viscacha);
}

На первый взгляд функции выглядят похоже - в чем разница?

print_kind_static() использует технику, называемую мономорфизацией (monomorphization), - для каждого животного, с которым вызывается функция, компилятор прозрачно генерирует специальную "скопированную" версию функции:

fn print_kind_static__chinchilla(animal: &Chinchilla) {
    println!("{}", Chinchilla::kind(animal));
}

fn print_kind_static__viscacha(animal: &Viscacha) {
    println!("{}", Viscacha::kind(animal));
}

fn main() {
    print_kind_static__chinchilla(&Chinchilla);
    print_kind_static__viscacha(&Viscacha);
}

Теперь вы понимаете, почему это называется статической диспетчеризацией - компилятор заменяет динамические типажи статическими типами.

У мономорфизации есть недостаток: она немного медленнее компилируется (компилятору приходится генерировать несколько функций вместо одной), но обычно она приводит к более быстрому и оптимизированному коду во время выполнения - это может иметь существенное значение для приложений, которые вызывают такие общие функции, скажем, миллион раз в секунду.

print_kind_dynamic(), с другой стороны, использует технику под названием vtable (virtual table - виртуальная таблица), когда для каждой реализации создается выделенная таблица сопоставлений с конкретными функциями:

// (это псевдокод для демонстрации концепции)

struct AnimalVtable {
    // Ссылка на определенную функцию `kind()`
    kind: fn(*const ()) -> &'static str,
}

const CHINCHILLA_VTABLE: AnimalVtable = AnimalVtable {
    kind: Chinchilla::kind,
};

const VISCACHA_VTABLE: AnimalVtable = AnimalVtable {
    kind: Viscacha::kind,
};

fn print_kind_dynamic(
    animal_obj: *const (),
    animal_vtable: &AnimalVtable,
) {
    println!("{}", animal_vtable.kind(animal_obj));
}

fn main() {
    print_kind_dynamic(&Chinchilla, &CHINCHILLA_VTABLE);
    print_kind_dynamic(&Viscacha, &VISCACHA_VTABLE);
}

Поскольку все реализации могут быть описаны через AnimalVtable, print_kind_dynamic() не нужно мономорфизировать - в зависимости от базового типа компилятор просто передаст другую виртуальную таблицу.

Недостатком такого подхода является то, что при каждом вызове функции print_kind_dynamic() мы должны проходить через эту дополнительную "прокси таблицу", что теоретически делает ее более медленной, чем print_kind_static(), однако в большинстве случаев разница несущественна.

Возвращаясь к исходному вопросу: почему не сделать where R: RngCore?

Поскольку мы не будем вызывать этот метод миллион раз в секунду, игра не стоит свеч.

Реализация:

pub struct RouletteWheelSelection;

impl SelectionMethod for RouletteWheelSelection {
    fn select<'a, I>(&self, rng: &mut dyn RngCore, population: &'a [I]) -> &'a I
    where
        I: Individual,
    {
        todo!()
    }
}

...мы можем сделать это вручную:

impl SelectionMethod for RouletteWheelSelection {
    fn select<'a, I>(&self, rng: &mut dyn RngCore, population: &'a [I]) -> &'a I
    where
        I: Individual,
    {
        let total_fitness: f32 = population
            .iter()
            .map(|individual| individual.fitness())
            .sum();

        // Это наивный подход для целей демонстрации - более эффективная
        // реализация будет вызывать `rng` только один раз
        loop {
            let indiv = population
                .choose(rng)
                .expect("получена пустая популяция");

            let indiv_share = indiv.fitness() / total_fitness;

            if rng.gen_bool(indiv_share as f64) {
                return indiv;
            }
        }
    }
}

...но идеальным кодом будет... его отсутствие!

Если полистать документацию rand, можно найти типаж SliceRandom. Если заглянуть в него, можно найти метод choose_weighted, который делает как раз то, что нам нужно:

use rand::seq::SliceRandom;
use rand::{Rng, RngCore};

/* ... */

impl SelectionMethod for RouletteWheelSelection {
    fn select<'a, I>(&self, rng: &mut dyn RngCore, population: &'a [I]) -> &'a I
    where
        I: Individual,
    {
        population
            .choose_weighted(rng, |individual| individual.fitness())
            .expect("получена пустая популяция")
    }
}

Помимо доверия разработчикам rand, как мы можем убедиться, что select_weighted() делает то, что нам нужно? Протестировав его!

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn roulette_wheel_selection() {
        todo!();
    }
}

Путь к TDD-нирване (test driven development - разработка через тестирование) усыпан розами, и мы вот-вот вкусим их шипы:

#[cfg(test)]
mod tests {
    use super::*;
    use rand::SeedableRng;
    use rand_chacha::ChaCha8Rng;

    #[test]
    fn roulette_wheel_selection() {
        let mut rng = ChaCha8Rng::from_seed(Default::default());

        let population = vec![ /* что здесь? */ ];
        let actual = RouletteWheelSelection::new().select(&mut rng, &population);

        assert!(/* что здесь? */);
    }
}

На данный момент у нас есть две проблемы:

1. Поскольку Individual - это типаж, не очень понятно, как сымитировать его для целей тестирования?
2. Поскольку select() возвращает отдельную особь, не очень понятно, как убедиться в ее произвольности?

Начнем с начала: создание фиктивных объектов для целей тестирования называется макетированием (mocking) - и хотя для Rust существуют решения для создания макетов, я никогда не был поклонником этой концепции.

Мое предложение, не требующее каких-либо внешних крейтов, - создать специальную структуру для тестирования:

#[cfg(test)]
mod tests {
    /* ... */

    #[derive(Clone, Debug)]
    struct TestIndividual {
        fitness: f32,
    }

    impl TestIndividual {
        fn new(fitness: f32) -> Self {
            Self { fitness }
        }
    }

    impl Individual for TestIndividual {
        fn fitness(&self) -> f32 {
            self.fitness
        }
    }

    /* ... */
}

...которую мы затем можем использовать следующим образом:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn roulette_wheel_selection() {
        /* ... */

        let population = vec![
            TestIndividual::new(2.0),
            TestIndividual::new(1.0),
            TestIndividual::new(4.0),
            TestIndividual::new(3.0),
        ];

        /* ... */
    }
}

А что насчет утверждения? Такой тест:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn roulette_wheel_selection() {
        /* ... */

        let actual = RouletteWheelSelection::new()
            .select(&mut rng, &population);

        assert!(actual, &population[2]);
    }
}

...не внушает доверия, поскольку не доказывает, что показатели приспособленности действительно учитываются. Совершенно некорректная реализация, такая как:

impl SelectionMethod for RouletteWheelSelection {
    fn select<'a, I>(/* ... */) -> &'a I
    where
        I: Individual,
    {
        &population[2]
    }
}

...успешно проходит такой тест!

К счастью, выход есть - поскольку мы хотим оценить вероятность, вместо того, чтобы вызывать select() один раз, мы можем сделать это несколько раз и посмотреть на гистограмму:

Ось X представляет элементы, ось Y - частоту.

#[cfg(test)]
mod tests {
    /* ... */
    use std::collections::BTreeMap;
    use std::iter::FromIterator;

    #[test]
    fn roulette_wheel_selection() {
        let mut rng = ChaCha8Rng::from_seed(Default::default());

        let population = vec![
            /* ... */
        ];

        let mut actual_histogram = BTreeMap::new();

        //          /--| Цифра 1000 взята с потолка;
        //          v  | возможно, 50 тоже подойдет
        for _ in 0..1000 {
            let fitness = RouletteWheelSelection
                .select(&mut rng, &population)
                .fitness() as i32;

            *actual_histogram
                .entry(fitness)
                .or_insert(0) += 1;
        }

        let expected_histogram = BTreeMap::from_iter([
            // (приспособленность, сколько раз эта приспособленность была выбрана)
            (1, 0),
            (2, 0),
            (3, 0),
            (4, 0),
        ]);

        assert_eq!(actual_histogram, expected_histogram);
    }
}

Обратите внимание, что при построении гистограммы мы преобразуем показатели приспособленности от f32 до i32:

let fitness = RouletteWheelSelection
    .select(&mut rng, &population)
    .fitness() as i32;

Мы должны это сделать, поскольку числа с плавающей точкой в Rust не реализуют типаж Ord, что делает невозможным их использование в качестве ключей BTreeMap:

use std::collections::BTreeMap;

fn main() {
    let mut map = BTreeMap::new();
    map.insert(1.0, "one point zero");
}

error[E0277]: the trait bound `{float}: Ord` is not satisfied
  |
  |     map.insert(1.0, "one point zero");
  |         ^^^^^^ the trait `Ord` is not implemented for `{float}`

Дело в том, что числа с плавающей точкой, как определено стандартом IEEE 754, не являются полностью упорядоченным набором, сравнение NaN проблематично, поскольку:

NaN != NaN

На практике это означает, что если бы мы могли вставить NaN в карту, то не только не могли бы получить его обратно, но это также могло бы сломать внутренние структуры данных BTreeMap, также сделав невозможным получение любого другого элемента. Кстати, это также верно для пользовательских реализаций Ord и PartialOrd - если они не будут удовлетворять асимметрии и транзитивности, вы быстро об этом пожалеете.

cargo test (или cargo test --workspace, если вы находитесь в каталоге виртуального манифеста) возвращает:

thread '...' panicked at 'assertion failed: `(left == right)`
  left: `{1: 98, 2: 202, 3: 278, 4: 422}`,
 right: `{1: 0, 2: 0, 3: 0, 4: 0}`'

...доказывая, что choose_weighted() работает так, как ожидается (более высокие показатели приспособленности выбираются чаще), поэтому скорректируем тест:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn roulette_wheel_selection() {
        /* ... */

        let expected_histogram = BTreeMap::from_iter(vec![
            // (приспособленность, сколько раз эта приспособленность была выбрана)
            (1, 98),
            (2, 202),
            (3, 278),
            (4, 422),
        ]);

        /* ... */
    }
}

Вуаля - мы проверили непроверяемое! Подготовив отбор, вспомним, на чем мы остановились:

impl GeneticAlgorithm {
    pub fn evolve<I>(&self, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */

        (0..population.len())
            .map(|_| {
                // TODO отбор
                // TODO скрещивание
                // TODO мутация
                todo!()
            })
            .collect()
    }
}

Теперь нам нужно выяснить, как передать туда SelectionMethod - я вижу два подхода:

1. С помощью параметра:

impl GeneticAlgorithm {
    pub fn evolve<I, S>(
        &self,
        population: &[I],
        selection_method: &S,
    ) -> Vec<I>
    where
        I: Individual,
        S: SelectionMethod,
    {
        /* ... */
    }
}

2. С помощью конструктора:

pub struct GeneticAlgorithm<S> {
    selection_method: S,
}

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    pub fn new(selection_method: S) -> Self {
        Self { selection_method }
    }

    pub fn evolve<I, S>(&self, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */
    }
}

Сталкиваясь с такими дилеммами, я задумываюсь о том, как часто пользователям придется менять этот объект.

Популяция обычно меняется при каждом вызове evolve(), поэтому ее удобно принимать через параметр. С другой стороны, алгоритм отбора обычно остается одинаковым для всей симуляции, поэтому пользователям будет удобнее предоставлять его через конструктор.

Теперь мы почти готовы вызвать метод отбора:

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(&self, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */

        (0..population.len())
            .map(|_| {
                let parent_a = self.selection_method.select(rng, population);
                let parent_b = self.selection_method.select(rng, population);

                // TODO скрещивание
                // TODO мутация
                todo!()
            })
            .collect()
    }
}

...единственное, чего нам не хватает, это ГПСЧ:

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(&self, rng: &mut dyn RngCore, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */
    }
}

Вам может быть интересно, почему мы передаем rng через аргумент, а не через конструктор, ведь генератор произвольных чисел не будет меняться для каждой популяции!

Не все так просто, рассмотрим другие способы написания этого кода:

1. Принимаем собственный ГПСЧ через конструктор:

pub struct GeneticAlgorithm<R> {
    rng: R,
}

impl<R> GeneticAlgorithm<R>
where
    R: RngCore,
{
    pub fn new(rng: R) -> Self {
        Self { rng }
    }
}

2. Принимаем заимствованный ГПСЧ через конструктор:

pub struct GeneticAlgorithm<'r> {
    rng: &'r mut dyn RngCore,
}

impl<'r> GeneticAlgorithm<'r> {
    pub fn new(rng: &'r mut dyn RngCore) -> Self {
        Self { rng }
    }
}

Первый подход я бы предложил в C# или Java, но не в Rust, потому что если мы переместим rng в конструктор, то не сможем использовать его в других местах приложения:

fn main() {
    let rng = /* ... */;
    let ga = GeneticAlgorithm::new(rng);

    // О нет, мы больше не можем использовать этот `rng`!
    if rng.gen_bool() {
        /* ... */
    } else {
        /* ... */
    }
}

Вы можете сказать, что то же самое происходит с SelectionMethod:

fn main() {
    let sp = RouletteWheelSelection::new();
    let ga = GeneticAlgorithm::new(sp);

    // О нет, мы больше не можем использовать этот `sp`!
    if sp.something() {
        /* ... */
    }
}

...но, на мой взгляд, разница в том, что Rng - это более универсальный типаж, который вполне может использоваться вне GeneticAlgorithm, чего нельзя сказать о SelectionMethod.

Что касается варианта &mut dyn RngCore, я считаю его худшим - он требует уникального заимствования (&mut) rng, так что он не только "блокирует" ГПСЧ на время жизни генетического алгоритма:

fn main() {
    let rng = /* ... */;
    let ga = GeneticAlgorithm::new(&mut rng);

    // О нет, мы по-прежнему не можем использовать этот `rng`!
    let population = if rng.gen_bool() {
        /* ... */
    } else {
        /* ... */
    };

    ga.evolve(population);
}

...но также ломает другие допустимые варианты использования, такие как:

struct Simulation {
    rng: ChaCha8Rng,
    ga: GeneticAlgoritm<'whats_this_lifetime??>,
}

impl Simulation {
    pub fn new_chacha() -> Self {
        let rng = ChaCha8Rng::from_seed(Default::default());
        let ga = GeneticAlgorithm::new(&mut rng);

        Self { rng, ga } // упс
    }
}

Разработка: скрещивание

Теперь, когда мы выбрали двух особей-родителей, пришло время для скрещивания.

Скрещивание (также известное как рекомбинация) берет двух особей и смешивает их, создавая новое решение:

По сравнению с простым созданием новых произвольных особей, скрещивание пытается сохранить знания. Идея в том, что скрещивание двух хороших особей обычно приводит к особи, которая является одновременно новой и, по крайней мере, такой же хорошей, как родительские особи. Это позволяет исследовать пространство поиска без риска потерять лучшие найденные на данный момент решения.

Как и в реальном мире, скрещивание на самом деле происходит не у отдельных особей, а скорее в их хромосомах - модное слово, обозначающее "кодирование решения":

Хромосома (также называемая генотипом, хотя я убежден, что биологам не нравится, когда эти понятия смешиваются) обычно состоит из генов, и ее структура зависит от решаемой задачи. Иногда хромосому удобно моделировать как битовый набор:

...иногда удобнее, чтобы хромосома содержала строку:

...или воспользуемся тем, что у нас есть - набором f32, представляющим веса нейронной сети:

#[derive(Clone, Debug)]
pub struct Chromosome {
    genes: Vec<f32>,
}

Вместо того, чтобы делать гены общедоступными (через pub genes​), мы предоставим несколько функций, позволяющих заглянуть внутрь хромосомы - это называется инкапсуляцией:

impl Chromosome {
    pub fn len(&self) -> usize {
        self.genes.len()
    }

    pub fn iter(&self) -> impl Iterator<Item = &f32> {
        self.genes.iter()
    }

    pub fn iter_mut(&mut self) -> impl Iterator<Item = &mut f32> {
        self.genes.iter_mut()
    }
}

Пользуясь случаем, рассмотрим некоторые интересные типажи стандартной библиотеки:

1. Типаж Index позволяет использовать оператор индексации [] для наших типов:

use std::ops::Index;

/* ... */

// ---
// | Это тип выражения внутри квадратных скобок,
// |
// | например, если мы реализуем `Index<&str>`, то сможем написать:
// |   chromosome["yass"]
// ------- v---v
impl Index<usize> for Chromosome {
    type Output = f32;

    fn index(&self, index: usize) -> &Self::Output {
        &self.genes[index]
    }
}

2. Типаж FromIterator позволяет использовать .collect() в наших типах:

// ---
// | Это тип элемента, который должен предоставить итератор для совместимости
// | с нашей хромосомой
// |
// | (иногда говорят, что это тип, который итератор *возвращает* (yields))
// |
// | Поскольку наша хромосома состоит из чисел с плавающей точкой, здесь
// | мы также ожидаем получить такие числа
// -------------- v-v
impl FromIterator<f32> for Chromosome {
    fn from_iter<T: IntoIterator<Item = f32>>(iter: T) -> Self {
        Self {
            genes: iter.into_iter().collect(),
        }
    }
}

3. Наконец, типаж IntoIterator работает противоположным образом - преобразует тип в итератор:

impl IntoIterator for Chromosome {
    type Item = f32;
    type IntoIter = std::vec::IntoIter<f32>;

    fn into_iter(self) -> Self::IntoIter {
        self.genes.into_iter()
    }
}

Для чего нужен std::vec::IntoIter<f32>?

Итератор - это просто тип, реализующий типаж Iterator:

struct Fibonacci {
    prev: u32,
    curr: u32,
}

impl Default for Fibonacci {
    fn default() -> Self {
        Self { prev: 0, curr: 1 }
    }
}

impl Iterator for Fibonacci {
    type Item = u32;

    fn next(&mut self) -> Option<u32> {
        let next = self.prev + self.curr;

        self.prev = self.curr;
        self.curr = next;

        Some(self.prev)
    }
}

fn main() {
    for number in Fibonacci::default().take(10) {
        println!("{}", number);
    }
}

Итак, для того, чтобы преобразовать тип в итератор, нужно знать целевой итерируемый тип. В нашем случае, поскольку Chromosome - это всего лишь оболочка для Vec, целевой тип - std::vec::IntoIter, что компилятор даже может нам подсказать:

struct Chromosome {
    genes: Vec<f32>,
}

impl IntoIterator for Chromosome {
    type Item = f32;
    type IntoIter = (); // мы намеренно используем здесь неправильный тип

    fn into_iter(self) -> Self::IntoIter {
        self.genes.into_iter()
    }
}

error[E0308]: mismatched types
   |
   | /* ... */
   |
   = note: expected unit type `()`
                 found struct `std::vec::IntoIter<f32>`

Однако вывести этот тип компилятору не всегда так просто, поскольку в нем учитываются все комбинаторы, такие как .filter() или .map():

struct Somethinger {
    values: Vec<f32>,
}

impl IntoIterator for Somethinger {
    type Item = f32;
    type IntoIter = ();

    fn into_iter(self) -> Self::IntoIter {
        self.values
            .into_iter()
            .filter(|value| *value > 0.0)
            .map(|value| value * 10.0)
    }
}

error[E0308]: mismatched types
   |
   | /* ... */
   |
   = note: expected unit type `()`
                 found struct `Map<Filter<std::vec::IntoIter<f32>, {closure}>, {closure}>`

Ночной Rust предлагает удобное решение этой проблемы - impl_trait_in_assoc_type:

#![feature(impl_trait_in_assoc_type)]

struct Somethinger {
    values: Vec<f32>,
}

impl IntoIterator for Somethinger {
    type Item = f32;
    type IntoIter = impl Iterator<Item = f32>;

    fn into_iter(self) -> Self::IntoIter {
        self.values
            .into_iter()
            .filter(|value| *value > 0.0)
            .map(|value| value * 10.0)
    }
}

...что по сути говорит: "Компилятор, выведи тип самостоятельно, пожалуйста".

Поскольку мы используем стабильную цепочку инструментов, мы не можем использовать эту функцию, но, к счастью, нам и не нужно.

Как я сказал несколько минут назад, скрещивание на самом деле происходит не у отдельных особей, а скорее в их хромосомах, что приводит нас к следующему:

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(/* ... */) -> Vec<I>
    where
        I: Individual,
    {
        (0..population.len())
            .map(|_| {
                let parent_a = self.selection_method.select(rng, population).chromosome();
                let parent_b = self.selection_method.select(rng, population).chromosome();

                /* ... */
            })
            .collect()
    }
}

/* ... */

pub trait Individual {
    fn fitness(&self) -> f32;
    fn chromosome(&self) -> &Chromosome;
}

/* ... */

#[cfg(test)]
mod tests {
    /* ... */

    impl Individual for TestIndividual {
        fn fitness(&self) -> f32 {
            self.fitness
        }

        fn chromosome(&self) -> &Chromosome {
            panic!("не поддерживается для TestIndividual")
        }
    }

    /* ... */
}

Что касается самого скрещивания, мы могли бы реализовать множество алгоритмов. Обычно лучше попробовать несколько и посмотреть, какой лучше всего подходит для решения конкретной задачи. Однако для простоты мы воспользуемся универсальным скрещиванием (uniform crossover), который можно описать с помощью одного рисунка:

Как и прежде, начнем с типажа:

pub trait CrossoverMethod {
    fn crossover(
        &self,
        rng: &mut dyn RngCore,
        parent_a: &Chromosome,
        parent_b: &Chromosome,
    ) -> Chromosome;
}

...и примитивной реализации:

pub struct UniformCrossover;

impl CrossoverMethod for UniformCrossover {
    fn crossover(
        &self,
        rng: &mut dyn RngCore,
        parent_a: &Chromosome,
        parent_b: &Chromosome,
    ) -> Chromosome {
        let mut child = Vec::new();
        let gene_count = parent_a.len();

        for gene_idx in 0..gene_count {
            let gene = if rng.gen_bool(0.5) {
                parent_a[gene_idx]
            } else {
                parent_b[gene_idx]
            };

            child.push(gene);
        }

        child.into_iter().collect()
    }
}

Ваш внутренний критик, возможно, заметил некоторые недостатки этого кода – и они действительно имеются!

Сначала добавим утверждение:

impl CrossoverMethod for UniformCrossover {
    fn crossover(/* ... */) -> Chromosome {
        assert_eq!(parent_a.len(), parent_b.len());

        /* ... */
    }
}

Во-вторых, воспользуемся комбинатором .zip(), который нам уже встречался в предыдущей статье:

impl CrossoverMethod for UniformCrossover {
    fn crossover(/* ... */) -> Chromosome {
        assert_eq!(parent_a.len(), parent_b.len());

        parent_a
            .iter()
            .zip(parent_b.iter())
            .map(|(&a, &b)| if rng.gen_bool(0.5) { a } else { b })
            .collect()
    }
}

Как аккуратно!

Обратите внимание, как, реализовав .iter() и FromIterator минуту назад, мы смогли сократить код до минимума, который передает суть универсального скрещивания.

Ваш внутренний критик все еще может считать, что чего-то не хватает... хм... а, конечно, тесты!

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn uniform_crossover() {
        let mut rng = ChaCha8Rng::from_seed(Default::default());
        let parent_a = todo!();
        let parent_b = todo!();
        let child = UniformCrossover.crossover(&mut rng, &parent_a, &parent_b);

        assert!(/* ... */);
    }
}

Мы хотим проверить, что child состоит из 50% parent_а + 50% parent_b.

Я предлагаю создать две разные хромосомы (они не обязательно должны быть произвольными, просто должны состоять из разных генов):

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn uniform_crossover() {
        /* ... */

        let parent_a: Chromosome = (1..=100).map(|n| n as f32).collect();
        let parent_b: Chromosome = (1..=100).map(|n| -n as f32).collect();

        // Первым предком будет:
        //   [1, 2, /* ... */, 100]
        //
        // Второй предок будет похож на первого, но с противоположными знаками:
        //   [-1, -2, /* ... */, -100]
        //
        // Как и в случае с гистограммой, точное число генов не имеет значения -
        // 100 просто хорошо представляет 100%, вот и все

        /* ... */
    }
}

...и затем сравнить, насколько child отличается от каждого предка:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn uniform_crossover() {
        /* ... */

        let child = UniformCrossover.crossover(&mut rng, &parent_a, &parent_b);

        // Количество разных генов между `child` и `parent_a`
        let diff_a = child.iter().zip(parent_a).filter(|(c, p)| *c != p).count();

        // Количество разных генов между `child` и `parent_b`
        let diff_b = child.iter().zip(parent_b).filter(|(c, p)| *c != p).count();

        assert_eq!(diff_a, 0);
        assert_eq!(diff_b, 0);
    }
}

cargo test говорит:

thread '...' panicked at 'assertion failed: `(left == right)`
  left: `49`,
 right: `0`'

...правим тест:

assert_eq!(diff_a, 49);

Другой cargo test "падает" на втором утверждении:

thread '...' panicked at 'assertion failed: `(left == right)`
  left: `51`,
 right: `0`'

...поэтому:

assert_eq!(diff_b, 51);

Получаем:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn uniform_crossover() {
        /* ... */

        assert_eq!(diff_a, 49);
        assert_eq!(diff_b, 51);
    }
}

Это означает, что наш child получил 49% своего генома от parent_a и 51% - от parent_b. Это в конечном итоге доказывает, что наше универсальное скрещивание выбирает гены от обоих родителей с равной вероятностью (мы не получили 50% на 50%, потому что вероятность есть вероятность).

Теперь мы можем передать CrossoverMethod следом за SelectionMethod:

pub struct GeneticAlgorithm<S> {
    selection_method: S,
    crossover_method: Box<dyn CrossoverMethod>,
}

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    pub fn new(
        selection_method: S,
        crossover_method: impl CrossoverMethod + 'static,
    ) -> Self {
        Self {
            selection_method,
            crossover_method: Box::new(crossover_method),
        }
    }

    /* ... */
}

В отличие от SelectionMethod::select(), CrossoverMethod::crossover() не содержит общих параметров, поэтому мы можем его упаковать (обернуть в Box). Другой подход может состоять в следующем:

pub struct GeneticAlgorithm<S, C> {
    selection_method: S,
    crossover_method: C,
}

impl<S, C> GeneticAlgorithm<S, C>
where
    S: SelectionMethod,
    C: CrossoverMethod,
{
    pub fn new(
        selection_method: S,
        crossover_method: C,
    ) -> Self {
        Self {
            selection_method,
            crossover_method,
        }
    }

    /* ... */
}

...компромисс здесь такой же, как в случае с T: Trait против dyn Trait (где Box<dyn Trait> соответствует динамической диспетчеризации).

Некоторые утверждают, что использование Box, которое имеет небольшое негативное влияние на производительность, делает код Rust менее идиоматичным.

Моя позиция заключается в том, что Box - это удобный механизм, потенциальный негатив которого во время выполнения компенсируется наличием кода, который легче поддерживать.

...и вызвать его:

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(&self, rng: &mut dyn RngCore, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */

        (0..population.len())
            .map(|_| {
                /* ... */

                let mut child = self.crossover_method.crossover(rng, parent_a, parent_b);

                /* ... */
            })
            .collect()
    }
}

Разработка: мутация

Теперь, когда у нас есть наполовину новая хромосома, пришло время внести немного разнообразия!

Мутация, наряду со скрещиванием и отбором, является третьим генетическим оператором - она берет хромосому и вносит в нее одно или несколько произвольных изменений:

Как и в настоящей эволюции, роль мутации заключается в поиске решений, которых не было в исходной популяции. Это также предотвращает застревание алгоритма в локальном оптимуме, поскольку меняет популяцию от одного поколения к другому.

Поскольку у нас уже реализована Chromosome, реализовать мутацию не составляет труда:

pub trait MutationMethod {
    fn mutate(&self, rng: &mut dyn RngCore, child: &mut Chromosome);
}

Мы будем использовать мутацию Гаусса (Gaussian mutation), которая представляет собой причудливый способ сказать: "Мы будем добавлять или вычитать произвольные числа из генома". В отличие от нашего метода отбора без параметров, мутация Гаусса требует указания двух аргументов:

#[derive(Clone, Debug)]
pub struct GaussianMutation {
    /// Вероятность изменения гена:
    /// - 0.0 = ни один ген не будет затронут
    /// - 1.0 = все гены будут затронуты
    chance: f32,

    /// Магнитуда этого изменения:
    /// - 0.0 =  затронутые гены не будут модифицированы
    /// - 3.0 = затронутые гены будут увеличены (+=) или уменьшены (-=), как минимум, на 3.0
    coeff: f32,
}

impl GaussianMutation {
    pub fn new(chance: f32, coeff: f32) -> Self {
        assert!(chance >= 0.0 && chance <= 1.0);

        Self { chance, coeff }
    }
}

impl MutationMethod for GaussianMutation {
    fn mutate(&self, rng: &mut dyn RngCore, child: &mut Chromosome) {
        for gene in child.iter_mut() {
            let sign = if rng.gen_bool(0.5) { -1.0 } else { 1.0 };

            if rng.gen_bool(self.chance as f64) {
                *gene += sign * self.coeff * rng.gen::<f32>();
            }
        }
    }
}

Что касается тестов, то вместо того, чтобы использовать fn test(), как раньше, на этот раз я хотел бы показать вам немного другой подход - поговорим о крайних случаях:

#[cfg(test)]
mod tests {
    /* ... */

    mod gaussian_mutation {
        mod given_zero_chance {
            mod and_zero_coefficient {
                #[test]
                fn does_not_change_the_original_chromosome() {
                    todo!();
                }
            }

            mod and_nonzero_coefficient {
                #[test]
                fn does_not_change_the_original_chromosome() {
                    todo!();
                }
            }
        }

        mod given_fifty_fifty_chance {
            mod and_zero_coefficient {
                #[test]
                fn does_not_change_the_original_chromosome() {
                    todo!();
                }
            }

            mod and_nonzero_coefficient {
                #[test]
                fn slightly_changes_the_original_chromosome() {
                    todo!();
                }
            }
        }

        mod given_max_chance {
            mod and_zero_coefficient {
                #[test]
                fn does_not_change_the_original_chromosome() {
                    todo!();
                }
            }

            mod and_nonzero_coefficient {
                #[test]
                fn entirely_changes_the_original_chromosome() {
                    todo!();
                }
            }
        }
    }
}

Мне понадобилось некоторое время, чтобы привыкнуть к такому названию тестов, но в конце концов я нашел это соглашение настолько полезным, что не могу не упомянуть о нем. Тесты с такой структурой стоят миллиона комментариев, потому что тесты, в отличие от комментариев, со временем не устаревают.

Во избежание копирования создадим вспомогательную функцию:

#[cfg(test)]
mod tests {
    /* ... */

    mod gaussian_mutation {
        use super::*;

        fn actual(chance: f32, coeff: f32) -> Vec<f32> {
            let mut rng = ChaCha8Rng::from_seed(Default::default());
            let mut child = vec![1.0, 2.0, 3.0, 4.0, 5.0].into_iter().collect();

            GaussianMutation::new(chance, coeff).mutate(&mut rng, &mut child);

            child.into_iter().collect()
        }

        /* ... */
    }
}

...остальное проще простого:

# ...

[dev-dependencies]
approx = "0.4"
rand_chacha = "0.3"

#[cfg(test)]
mod tests {
    /* ... */

    mod gaussian_mutation {
        /* ... */

        mod given_zero_chance {
            use approx::assert_relative_eq;

            fn actual(coeff: f32) -> Vec<f32> {
                super::actual(0.0, coeff)
            }

            mod and_zero_coefficient {
                use super::*;

                #[test]
                fn does_not_change_the_original_chromosome() {
                    let actual = actual(0.0);
                    let expected = vec![1.0, 2.0, 3.0, 4.0, 5.0];

                    assert_relative_eq!(actual.as_slice(), expected.as_slice());
                }
            }

            mod and_nonzero_coefficient {
                use super::*;

                #[test]
                fn does_not_change_the_original_chromosome() {
                    let actual = actual(0.5);
                    let expected = vec![1.0, 2.0, 3.0, 4.0, 5.0];

                    assert_relative_eq!(actual.as_slice(), expected.as_slice());
                }
            }
        }

        /* ... */
    }
}

Попробуйте реализовать остальные тесты самостоятельно.

Теперь мы можем передать MutationMethod следом за SelectionMethod. Внутри MutationMethod::mutate() нет дженериков, поэтому давайте не будем колебаться в отношении Box:

pub struct GeneticAlgorithm<S> {
    selection_method: S,
    crossover_method: Box<dyn CrossoverMethod>,
    mutation_method: Box<dyn MutationMethod>,
}

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    pub fn new(
        selection_method: S,
        crossover_method: impl CrossoverMethod + 'static,
        mutation_method: impl MutationMethod + 'static,
    ) -> Self {
        Self {
            selection_method,
            crossover_method: Box::new(crossover_method),
            mutation_method: Box::new(mutation_method),
        }
    }

    /* ... */
}

...и затем:

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(/* ... */) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */

        (0..population.len())
            .map(|_| {
                /* ... */

                self.mutation_method.mutate(rng, &mut child);

                /* ... */
            })
            .collect()
    }
}

Разработка: создание особей

Наш child имеет тип Chromosome, а вектор, который мы возвращаем, - Vec<I>, поэтому последнее, чего нам не хватает, - это возможности конвертировать генотип обратно в особь:

pub trait Individual {
    fn create(chromosome: Chromosome) -> Self;

    /* ... */
}

/* ... */

#[cfg(test)]
mod tests {
    /* ... */

    impl Individual for TestIndividual {
        fn create(chromosome: Chromosome) -> Self {
           todo!()
        }

        /* ... */
    }
}

...и затем вуаля:

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(&self, rng: &mut dyn RngCore, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        assert!(!population.is_empty());

        (0..population.len())
            .map(|_| {
                let parent_a = self.selection_method.select(rng, population).chromosome();
                let parent_b = self.selection_method.select(rng, population).chromosome();
                let mut child = self.crossover_method.crossover(rng, parent_a, parent_b);

                self.mutation_method.mutate(rng, &mut child);

                I::create(child)
            })
            .collect()
    }
}

Тестирование

Пришло время, пожалуй, для самой захватывающей части этой статьи: теста, который докажет всем, что наш .evolve() работает, и что мы понимаем, что делаем.

Начнем с настройки нашего TestIndividual так, чтобы вместо panic!() он фактически реализовывал ::create() и .chromosome().

Некоторые тесты, например, для RouletteWheelSelection, вообще не заботятся о генах, поэтому мы получим дополнительные баллы за изобретение решения, которое не потребует модификации работающих тестов.

Я предлагаю изменить TestIndividual со struct на enum с двумя разными вариантами:

#[cfg(test)]
mod tests {
    /* ... */

    #[derive(Clone, Debug)]
    enum TestIndividual {
        /// Для тестов, которым нужен доступ к хромосоме
        WithChromosome { chromosome: Chromosome },

        /// Для тестов, которым не нужен доступ к хромосоме
        WithFitness { fitness: f32 },
    }

    impl TestIndividual {
        fn new(fitness: f32) -> Self {
            Self::WithFitness { fitness }
        }
    }

    impl Individual for TestIndividual {
        fn create(chromosome: Chromosome) -> Self {
            Self::WithChromosome { chromosome }
        }

        fn chromosome(&self) -> &Chromosome {
            match self {
                Self::WithChromosome { chromosome } => chromosome,

                Self::WithFitness { .. } => {
                    panic!("не поддерживается для TestIndividual::WithFitness")
                }
            }
        }

        fn fitness(&self) -> f32 {
            match self {
                Self::WithChromosome { chromosome } => {
                    chromosome.iter().sum()
                    // ^ самая простая на свете фитнес-функция:
                    // мы просто складываем все гены вместе
                }

                Self::WithFitness { fitness } => *fitness,
            }
        }
    }

    /* ... */
}

Пока мы здесь, выведем (derive) PartialEq - нам это пригодится через мгновение:

#[cfg(test)]
mod tests {
    /* ... */

    #[derive(Clone, Debug, PartialEq)]
    pub enum TestIndividual {
        /* ... */
    }

    /* ... */

    impl PartialEq for Chromosome {
        fn eq(&self, other: &Self) -> bool {
            approx::relative_eq!(self.genes.as_slice(), other.genes.as_slice())
        }
    }

    /* ... */
}

Что касается теста, начнем с нескольких особей, эволюционируем их в течение пары поколений и посмотрим, как они в итоге будут выглядеть:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn genetic_algorithm() {
        let mut rng = ChaCha8Rng::from_seed(Default::default());

        let ga = GeneticAlgorithm::new(
            RouletteWheelSelection,
            UniformCrossover,
            GaussianMutation::new(0.5, 0.5),
        );

        let mut population = vec![
            /* TODO */
        ];

        // Мы запускаем `.evolve()` несколько раз, чтобы легче было заметить разницу
        // между входной и выходной популяциями.
        //
        // 10 взято с потолка, с тем же успехом мы можем взять 5, 20 или даже
        // 1000 поколений: единственное, что будет меняться - магнитуда
        // разницы между популяциями.
        for _ in 0..10 {
            population = ga.evolve(&mut rng, &population);
        }

        let expected_population = vec![
            /* TODO */
        ];

        assert_eq!(population, expected_population);
    }

    /* ... */
}

Мы собираемся создавать несколько особей за раз, поэтому нам нужна вспомогательная функция:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn genetic_algorithm() {
        fn individual(genes: &[f32]) -> TestIndividual {
            TestIndividual::create(genes.iter().cloned().collect())
        }

        /* ... */
    }

    /* ... */
}

...и теперь:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn genetic_algorithm() {
        /* ... */

        let mut population = vec![
            individual(&[0.0, 0.0, 0.0]),
            individual(&[1.0, 1.0, 1.0]),
            individual(&[1.0, 2.0, 1.0]),
            individual(&[1.0, 2.0, 4.0]),
        ];

        /* ... */

        let expected_population = vec![
            individual(&[0.0, 0.0, 0.0, 0.0]),
            individual(&[0.0, 0.0, 0.0, 0.0]),
            individual(&[0.0, 0.0, 0.0, 0.0]),
            individual(&[0.0, 0.0, 0.0, 0.0]),
        ];

        /* ... */
    }
}

4 особи ровно по 3 гена каждая - это показалось мне оптимальным.

cargo test:

thread '...' panicked at 'assertion failed: `(left == right)`
  left: `[WithChromosome { ... }, WithChromosome { ... }, ... ]`,
 right: `[WithChromosome { ... }, WithChromosome { ... }, ... ]`,

Копируем и вставляем фактические гены из left в expected_population:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn genetic_algorithm() {
        /* ... */

        let expected_population = vec![
            individual(&[0.44769490, 2.0648358, 4.3058133]),
            individual(&[1.21268670, 1.5538777, 2.8869110]),
            individual(&[1.06176780, 2.2657390, 4.4287640]),
            individual(&[0.95909685, 2.4618788, 4.0247330]),
        ];

        /* ... */
    }
}

Да... ха-ха-ха... да... у нас есть... числа?

Не вызывает сомнений тот факт, что мы получили какой-то результат, но откуда нам знать, что эти четыре особи на самом деле лучше, чем те, с которых мы начали?

Что ж, мы можем сравнить их показатели приспособленности!

// В данном случае `показатель приспособленности` означает `среднее значение генов` согласно нашей реализации
// внутри `TestIndividual::fitness()`

let population = vec![
    individual(&[/* ... */]), // приспособленность = 0.0
    individual(&[/* ... */]), // приспособленность = 1.0
    individual(&[/* ... */]), // приспособленность ~= 1.33
    individual(&[/* ... */]), // приспособленность ~= 2.33
];

let expected_population = vec![
    individual(&[/* ... */]), // приспособленность ~= 6.8
    individual(&[/* ... */]), // приспособленность ~= 5.7
    individual(&[/* ... */]), // приспособленность ~= 7.8
    individual(&[/* ... */]), // приспособленность ~= 7.4
];

Работает! Работает! Наш генетический алгоритм - высший хищник информатики!

Мы получили более высокие показатели приспособленности, а это значит, что наши особи стали лучше и все работает так, как задумано:

1. Благодаря выбору колеса рулетки худшее решение, [0,0, 0,0, 0,0], было отброшено.
2. Благодаря универсальному скрещиванию средний показатель приспособленности вырос от 3.5 до 7 (!).
3. Благодаря мутации Гаусса мы видим гены (числа), которых не было в начальной популяции.

Впрочем, можете мне не верить, попробуйте закомментировать разные части алгоритма:

// self.mutation_method.mutate(rng, &mut child);

...и посмотрите, как это повлияет на выходную популяцию.

Заключительные мысли

На данный момент, узнав так много всего по пути, мы реализовали два отдельных компонента: нейронную сеть и генетический алгоритм.

В следующий части мы объединим эти алгоритмы и реализуем великолепный пользовательский интерфейс, который позволит нам видеть больше, чем просто наборы чисел с плавающей точкой - здесь в игру вступят JavaScript и WebAssembly.

Часть 4.1

В сегодняшнем выпуске:

Сексуальные многоугольники

Сертифицированные ISO диаграммы ASCII

------------
| \...%....|
|   \......|
|    @>....|
|      \...|
|        \.|
------------

Клевые числа

После того, как мы реализовали нейронную сеть и генетический алгоритм, нас ждет самая восхитительная часть: моделирование экосистемы и отображение танцующих треугольников на наших экранах!

Предупреждение: эта статья содержит код JavaScript.

Не беспокойтесь, если JavaScript (далее также - JS) или HTML вам незнакомы, я постараюсь объяснить все концепции по ходу дела.

Проект

У нас есть struct NeuralNetwork и struct GeneticAlgorithm, а как насчет struct Eye или struct World? Ведь у наших птиц должны быть глаза и место для жизни!

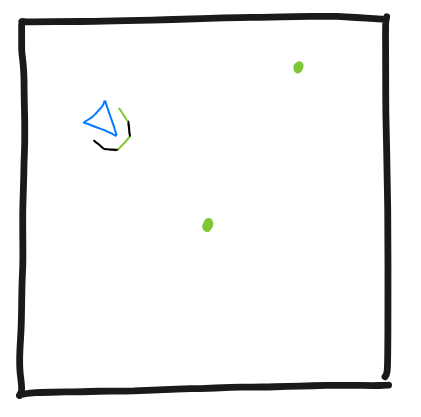
Вот чем мы будем заниматься сегодня и в следующей заключительной статье: мы реализуем функции, которые будут определять, что видит птица или как она двигается. Мы также создадим пользовательский интерфейс, который позволит нам видеть больше, чем сухие числа - пришло время лучше задействовать нашу зрительную кору!

Если вам нравятся диаграммы, то мы стремимся к следующему:

Как всегда, помимо кодирования, мы также исследуем, что именно происходит под всеми слоями абстракций, которые нам встретятся. Если вы не хотите этого знать, не стесняйтесь пропускать соответствующие разделы.

Готовы? Тогда вперед.

Предварительные условия

Для работы с WebAssembly (далее также - WA) нам понадобятся два дополнительных инструмента:

• npm (Cargo для JS)
• wasm-pack (набор инструментов, облегчающий компиляцию WA в Rust)

Прежде чем продолжить, установите эти инструменты.

Привет, WA (Rust)!

Начнем с создания нового крейта, отвечающего за взаимодействие с фронтендом:

Формально такой модуль для "общения с другой системой" называется мостом (bridge) или модулем взаимодействия (interop).

cd shorelark/libs
cargo new simulation-wasm --lib --name lib-simulation-wasm

Для того, чтобы наш крейт поддерживал WA, нам нужно добавить в его манифест 2 вещи:

1. Нам нужно установить crate-type в значение cdylib:

[package]
# ...

[lib]
crate-type = ["cdylib"]

Компилятор преобразует код в нечто, а crate-type определяет, каким будет это нечто, также называемое артефактом:

• crate-type = ["bin"] означает: компилятор, пожалуйста, сгенерируй программу (например, файл .exe на Windows)
• create-type = ["lib"] означает: компилятор, пожалуйста, сгенерируй библиотеку

Где:

• программа - это нечто, что мы можем вызывать напрямую (например, в терминале) библиотека - код, предоставляющий функционал для других крейтов

Тип, который нам нужно использовать, cdylib, обозначает динамическую библиотеку C и сообщает компилятору следующее:

• он должен экспортировать только те функции, которые предназначены для вызова извне, игнорируя внутренние особенности Rust.

Это предотвращает раздувание библиотеки "бесполезными" метаданными, что важно для WA (мы не хотим, чтобы наши пользователи обанкротились из-за счетов за Интернет, не так ли?).

• он должен генерировать динамическую библиотеку, т.е. фрагмент кода, который будет вызываться кем-то другим.

Это необходимо для WA, потому что, как вы вскоре увидите, наш код Rust не будет работать автономно: он будет предоставлен в полное распоряжение JS.

На практике это означает, что у нас не будет никаких fn main() { ...​ }, а будет pub fn do_something() { ...​ }.

2. Нам нужно включить wasm-bindgen в наши зависимости:

# ...

[dependencies]
wasm-bindgen = "0.2"

wasm-bindgen предоставляет типы и макросы, упрощающие написание кода, компилируемого в WA.

Rust + WA можно писать и без него, просто это будет менее удобным.

С настройками закончили, давайте писать код!

Поскольку создание симуляции займет некоторое время, а было бы неплохо увидеть, как что-то работает как можно скорее, я предлагаю начать с создания функции, которую мы сможем вызывать из JS, просто для того, чтобы убедиться, что эта штука на WA не обман:

pub fn whos_that_dog() -> String {
    "Mister Peanutbutter".into()
}

Если бы мы создавали обычный крейт для публикации на crates.io, этого было бы достаточно, но для WA нам нужно добавить еще одну вещь, #[wasm_bindgen]:

use wasm_bindgen::prelude::*;

#[wasm_bindgen]
pub fn whos_that_dog() -> String {
    "Mister Peanutbutter".into()
}

Немного упрощая, можно сказать, что процедурный макрос #[wasm_bindgen] сообщает компилятору, что мы хотим экспортировать данную функцию или тип, т.е. сделать ее видимой на стороне JS.

Все символы Rust в конечном итоге компилируются в WA, но только те, к которым добавлен #[wasm_bindgen], могут вызываться напрямую из JS.

Чтобы создать крейт WA, воспользуемся только что установленным wasm-pack:

cd simulation-wasm
wasm-pack build

Разница между обычным cargo и wasm-pack заключается в том, что последний не только компилирует код, но и генерирует множество полезных файлов JS, которые в противном случае нам пришлось бы писать вручную. Эти файлы можно найти внутри только что созданной директории pkg:

ls -l pkg
total 36
-rw-r--r-- 1 pwy   110 Apr  2 17:20 lib_simulation_wasm.d.ts
-rw-r--r-- 1 pwy   184 Apr  2 17:20 lib_simulation_wasm.js
-rw-r--r-- 1 pwy  1477 Apr  2 17:20 lib_simulation_wasm_bg.js
-rw-r--r-- 1 pwy 13155 Apr  2 17:20 lib_simulation_wasm_bg.wasm
-rw-r--r-- 1 pwy   271 Apr  2 17:20 lib_simulation_wasm_bg.wasm.d.ts
-rw-r--r-- 1 pwy   356 Apr  2 17:20 package.json

Кратко рассмотрим, что у нас есть:

• package.json - это как Cargo.toml для npm, содержит метаданные модуля:

{
  "name": "lib-simulation-wasm",
  "version": "0.1.0",
  /* ... */
}

• lib_simulation_wasm.d.ts содержит определения типов (forward declarations), которые используются IDE для подсказок:

/**
 * @returns {string}
 */
export function whos_that_dog(): string;

• lib_simulation_wasm_bg.wasm содержит байт-код WA нашего крейта; это похоже на .dll или .so, и мы можем использовать wabt для его изучения (в основном для развлечения, полагаю):

(module
  (func (type 1) (param i32) (result i32)
    (local i32 i32 i32 i32)
    global.get 0
    i32.const 16
    i32.sub
    local.tee 11
    ;; ...

• lib_simulation_wasm_bg.js содержит довольно пугающий код, который фактически вызывает нашу библиотеку WA:

/**
 * @returns {string}
 */
export function whos_that_dog() {
    try {
        const retptr = wasm.__wbindgen_add_to_stack_pointer(-16);
        wasm.whos_that_dog(retptr);
        var r0 = getInt32Memory0()[retptr / 4 + 0];
        var r1 = getInt32Memory0()[retptr / 4 + 1];
        return getStringFromWasm0(r0, r1);
    } finally {
        wasm.__wbindgen_add_to_stack_pointer(16);
        wasm.__wbindgen_free(r0, r1);
    }
}

Если наш код Rust почти ничего не делает:

pub fn whos_that_dog() -> String {
    "Mister Peanutbutter".into()
}

...почему сгенерированного кода так много?

Вкратце, это связано с тем, что WA не поддерживает строки, и wasm-pack пытается это прозрачно обойти.

Но сначала терминология:

• когда мы перемещаем значение из одной функции в другую, когда обе функции работают в разных средах и/или когда они написаны на разных языках, мы заставляем значение пересечь границу интерфейса внешней функции (foreign function interface, FFI):

В этом случае мы говорим, что функция whos_that_dog() возвращает строку, которая пересекает границу FFI из Rust (где она создается) в JS (где она используется).

Пересечение границы FFI - это большое дело, потому что разные языки часто по-разному представляют объекты в памяти. Поэтому, даже если struct Foo в Rust и class Foo в JS на первый взгляд выглядят одинаково, в памяти они хранятся по-разному.

Это означает, что когда мы хотим отправить значение из одного языка в другой, мы не можем просто сказать: "Эй, по адресу 0x0000CAFE есть несколько байтов — это Foo". Вместо этого, нам нужно преобразовать это значение в то, что сможет понять другая сторона:

• преобразование значения в другое представление называется сериализацией (serialization).

Например, такой тип:

struct Foo {
    value: String,
}

...может быть сериализован в, скажем, такой JSON:

{
  "value": "Hi!"
}

...который затем может быть легко десериализован (deserialize) на стороне JS:

const foo = JSON.parse('{ "value": "Hi!" }');
console.log(foo);

Сериализация не ограничивается удобочитаемыми форматами, такими как JSON, YAML или XML. Существуют также такие форматы как Protocol Buffers.

Хотя и Rust, и JS поддерживают строки, WA понимает в основном числа. Это означает, что все функции, которые мы экспортируем через #[wasm_bindgen], могут принимать и возвращать максимум несколько чисел (с точки зрения WA).

Это означает, что для возврата строки wasm-pack пришлось проявить творческий подход:

pub extern "C" fn __wasm_bindgen_generated_whos_that_dog()
    -> <String as ReturnWasmAbi>::Abi
{
    let _ret = { whos_that_dog() };
    <String as ReturnWasmAbi>::return_abi(_ret)
}

Это известно как шим (shim) (или функция склеивания (glue-function), или склеивающий код (glue-code)).

Это конвертирует строку Rust в пару чисел:

• r0, определяющее локацию возвращаемой строки в памяти (старый-добрый указатель)
• r1, определяющее длину возвращаемой строки

Эти два числа затем используются функцией getStringFromWasm0() для воссоздания ("десериализации") строки на стороне JS — и все это без нашего участия.

Итак, мы скомпилировали крейт, но как его запустить?

Привет, WA (JS)!

Время фронтенда!

Для запуска фронтенда вернемся в корневую директорию проекта:

cd ../..

Для настройки фронтенда также требуется немного шаблонного кода. К счастью, на этот раз мы можем использовать команду npm init, чтобы скопировать и вставить для нас шаблон фронтенда WA:

npm init wasm-app www

Выполнение данной команды приводит к генерации директории www со следующими файлами:

ls -l www
total 248
-rw-r--r-- 1 pwy  10850 Apr  2 17:24 LICENSE-APACHE
-rw-r--r-- 1 pwy   1052 Apr  2 17:24 LICENSE-MIT
-rw-r--r-- 1 pwy   2595 Apr  2 17:24 README.md
-rw-r--r-- 1 pwy    279 Apr  2 17:24 bootstrap.js
-rw-r--r-- 1 pwy    297 Apr  2 17:24 index.html
-rw-r--r-- 1 pwy     56 Apr  2 17:24 index.js
-rw-r--r-- 1 pwy 209434 Apr  2 17:24 package-lock.json
-rw-r--r-- 1 pwy    937 Apr  2 17:24 package.json
-rw-r--r-- 1 pwy    311 Apr  2 17:24 webpack.config.js

Кратко рассмотрим их.

Знай своего врага

Точкой входа (main.rs в Rust), является index.html:

<!DOCTYPE html>
<html>
  <head>
    <meta charset="utf-8">
    <title>Hello wasm-pack!</title>
  </head>

  <body>
    <script src="./bootstrap.js"></script>
  </body>
</html>

Краткий обзор HTML:

• <something> называется тегом (tag)
• теги бывают открывающие (<something>) и закрывающие (</something>)
• тег может содержать атрибуты: key="value"
• тег может содержать детей (children) (другие теги)

В общем, документ HTML описывает представление веб-страницы в виде дерева (это называется объектным представлением документа (document object model, DOM)):

html
├── head
│   ├── meta
│   └── title
└── body
    └── script

...которое браузер анализирует, пытаясь сделать из него что-то приятное.

Каждый тег имеет определенное значение:

• html оборачивает весь документ
• head содержит метаданные документа (такие как язык или заголовок)
• body оборачивает содержимое документа
• script загружает и выполняет файл JS
• p (отсутствует в примере) оборачивает текст
• b (отсутствует в примере) делает текст полужирным и т.д.

<body>
  <p>yes... ha ha ha... <b>yes!</b></p>
</body>

Мы видим, что наша страница делает не так уж много - самое главное, что она загружает bootstrap.js:

import("./index.js")
  .catch(e => console.error("Error importing `index.js`:", e));

import - это как use или extern crate в Rust. В отличие от Rust, в JS import может использоваться как инструкция, т.е. может возвращать значения. На псевдокоде Rust это будет выглядеть так:

(mod "./index.js")
    .await
    .map_err(|e| {
        eprintln!("Error importing `index.js`:", e);
    });

Мы видим, что этот код загружает index.js, поэтому заглянем туда:

import * as wasm from "hello-wasm-pack";
//                     ^-------------^
//                      определяется в package.json

wasm.greet();

Этот import больше напоминает extern crate:

extern crate hello_wasm_pack as wasm;

wasm::greet();

Если говорить о коде приложения, то это все.

В директории www имеется еще один интересный файл - webpack.config.js:

const CopyWebpackPlugin = require("copy-webpack-plugin");
const path = require('path');

module.exports = {
  entry: "./bootstrap.js",
  output: {
    path: path.resolve(__dirname, "dist"),
    filename: "bootstrap.js",
  },
  mode: "development",
  plugins: [
    new CopyWebpackPlugin(['index.html'])
  ],
};

Этот файл содержит настройки для webpack, который похож на Cargo для JS.

Давайте кое-что проясним:

• npm управляет зависимостями
• webpack собирает приложение

В Rust все это делает Cargo (как удобно!), но в JS для этого нужны отдельные инструменты.

Мы узнали своего врага, что дальше?

Обменявшись любезностями с файловой системой, вернемся к делу:

1. На данный момент npm не знает о lib-simulation-wasm, исправим это:

// www/package.json
{
  /* ... */
  "devDependencies": {
    "lib-simulation-wasm": "file:../libs/simulation-wasm/pkg",
    /* ... */
  }
}

2. Сообщаем npm об этом изменении:

cd www
npm install

3. Пришло время index.js:

import * as sim from "lib-simulation-wasm";

alert("Who's that dog? " + sim.whos_that_dog() + "!");

Здесь нет function main() { }, потому что в JS она не нужна, весь код выполняется сверху вниз (более или менее).

4. Запускаем приложение (по сути, это cargo run):

npm run start

...
ℹ ｢wds｣: Project is running at http://localhost:8080/
...

Если выполнение этой команды проваливается с error:0308010C, возможно, вы используете слишком новую версию Node.js. Попробуйте запустить команду так:

NODE_OPTIONS=--openssl-legacy-provider npm run start

Открываем http://localhost:8080/ в браузере:

Ура!

Сервер, запущенный с помощью npm run start, автоматически реагирует на изменения.

Если вы хотите изменить сообщение, вернитесь в lib.rs, сделайте, что хотите, запустите wasm-pack build, и через несколько секунд сайт должен автоматически перезагрузиться.

То же самое относится к HTML и JS, хотя в этом случае повторно запускать wasm-pack не нужно.

Привет, WA (заключение)!

Итак... Что это все значит?

Конечно, отображение предупреждающего сообщения не сделает нас лауреатами Нобелевской премии, но нашей целью было быстро заставить что-то работать, и мы ее достигли.

В следующем разделе мы начнем заниматься симуляцией.

Привет, симуляция!

Как обычно, начинаем с создания нового крейта:

cd ../libs
cargo new simulation --lib --name lib-simulation

Этот крейт будет содержать движок нашей симуляции:

pub struct Simulation;

Чтобы не создавать дизайн из воздуха, вспомним предыдущий рисунок:

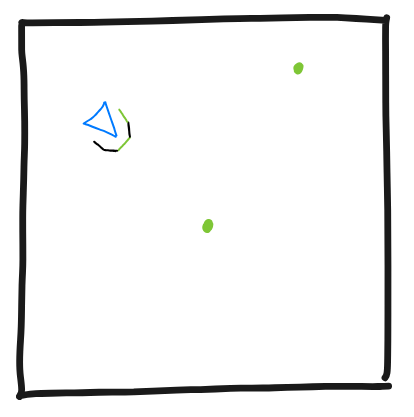
Что мы здесь видим? Конечно, мы видим здесь мир:

pub struct Simulation {
    world: World,
}

#[derive(Debug)]
pub struct World;

...который содержит животных (птиц!) и еду (богатую белками и клетчаткой!):

/* ... */

#[derive(Debug)]
pub struct World {
    animals: Vec<Animal>,
    foods: Vec<Food>,
}

#[derive(Debug)]
pub struct Animal;

#[derive(Debug)]
pub struct Food;

...которые находятся в некоторых координатах:

/* ... */

#[derive(Debug)]
pub struct Animal {
    position: ?,
}

#[derive(Debug)]
pub struct Food {
    position: ?,
}

Наш мир является двумерным, что приводит нас к:

/* ... */

#[derive(Debug)]
pub struct Animal {
    position: Point2,
}

#[derive(Debug)]
pub struct Food {
    position: Point2,
}

#[derive(Debug)]
pub struct Point2 {
    x: f32,
    y: f32,
}

Кроме того, животные имеют определенный угол поворота...

До сих пор почти весь код мы писали вручную.

Сейчас, когда дело дошло до некоторых математических структур данных, мне бы не хотелось изобретать велосипед - отчасти потому, что ручное написание кода почти ничему нас не научит:

#[derive(Copy, Clone, Debug)]
pub struct Point2 {
    x: f32,
    y: f32,
}

impl Point2 {
    pub fn new(...) -> Self {
        /* ... */
    }

    /* ... */
}

impl Add<Point2> for Point2 {
    /* ... */
}

impl Sub<Point2> for Point2 {
    /* ... */
}

impl Mul<Point2> for f32 {
    /* ... */
}

impl Mul<f32> for Point2 {
    /* ... */
}

#[cfg(test)]
mod tests {
    /* ... */
}

...и отчасти потому, что я хочу познакомить вас с крейтом, который мне очень нравится: nalgebra!

Цитируя их документацию:

nalgebra - это библиотека линейной алгебры, написанная для Rust:

• линейная алгебра общего назначения (все еще не хватает многих функций...)
• компьютерная графика в реальном времени
• компьютерная физика в реальном времени

Другими словами, nalgebra - это математика для людей, сделанная правильно, хорошо работающая с WA.

nalgebra предоставляет множество инструментов: от простых функций, таких как clamp, до довольно сложных структур, таких как кватернионы, и до нашей любимой точки.

Редактируем манифест:

# libs/simulation/Cargo.toml
# ...

[dependencies]
nalgebra = "0.26"

...и затем:

use nalgebra as na;
// --------- ^^
// | Такой вид импорта называется псевдонимом (alias).
// | Псевдонимом `nalgebra` является `na`.
// ---

/* ... */

#[derive(Debug)]
pub struct Animal {
    position: na::Point2<f32>,
}

#[derive(Debug)]
pub struct Food {
    position: na::Point2<f32>,
}

На чем мы остановились? Ах да, животные имеют определенный угол вращения и скорость:

/* ... */

#[derive(Debug)]
pub struct Animal {
    position: na::Point2<f32>,
    rotation: na::Rotation2<f32>,
    speed: f32,
}

/* ... */

В целом вращение и скорость также можно представить вместе в виде вектора:

#[derive(Debug)]
pub struct Animal {
    position: na::Point2<f32>,
    velocity: na::Vector2<f32>,
}

Мы продолжим использовать два отдельных поля, потому что это облегчит выполнение некоторых вычислений в будущем, но если вы хотите приключений...​

Теперь, когда у нас есть несколько моделей, было бы неплохо их как-нибудь сконструировать, поэтому:

# ...

[dependencies]
nalgebra = "0.26"
rand = "0.8"

...и пока мы здесь, включим поддержку rand в nalgebra - она нам пригодится через мгновение:

# ...

[dependencies]
nalgebra = { version = "0.26", features = ["rand-no-std"] }
rand = "0.8"

Начнем с нескольких элементарных конструкторов, которые просто все рандомизируют:

use nalgebra as na;
use rand::{Rng, RngCore};

/* ... */

impl Simulation {
    pub fn random(rng: &mut dyn RngCore) -> Self {
        Self {
            world: World::random(rng),
        }
    }
}

impl World {
    pub fn random(rng: &mut dyn RngCore) -> Self {
        let animals = (0..40)
            .map(|_| Animal::random(rng))
            .collect();

        let foods = (0..60)
            .map(|_| Food::random(rng))
            .collect();

        // ^ Наш алгоритм позволяет животным и еде накладываться друг на друга,
        // | это не идеально, но для наших целей сойдет.
        // |
        // | Более сложное решение может быть основано, например, на
        // | избыточной выборке сглаживания:
        // |
        // | https://en.wikipedia.org/wiki/Supersampling
        // ---

        Self { animals, foods }
    }
}

impl Animal {
    pub fn random(rng: &mut dyn RngCore) -> Self {
        Self {
            position: rng.gen(),
            // ------ ^-------^
            // | Если бы не `rand-no-std`, нам пришлось бы делать
            // | `na::Point2::new(rng.gen(), rng.gen())`
            // ---

            rotation: rng.gen(),
            speed: 0.002,
        }
    }
}

impl Food {
    pub fn random(rng: &mut dyn RngCore) -> Self {
        Self {
            position: rng.gen(),
        }
    }
}

Геттер - это функция для доступа к состоянию объекта, реализуем парочку:

/* ... */

impl Simulation {
    /* ... */

    pub fn world(&self) -> &World {
        &self.world
    }
}

impl World {
    /* ... */

    pub fn animals(&self) -> &[Animal] {
        &self.animals
    }

    pub fn foods(&self) -> &[Food] {
        &self.foods
    }
}

impl Animal {
    /* ... */

    pub fn position(&self) -> na::Point2<f32> {
        // ------------------ ^
        // | Нет необходимости возвращать ссылку, поскольку `na::Point2` является копируемым (реализует типаж `Copy`).
        // |
        // | (он настолько маленький, что клонирование дешевле, чем возня с ссылками)
        // ---

        self.position
    }

    pub fn rotation(&self) -> na::Rotation2<f32> {
        self.rotation
    }
}

impl Food {
    /* ... */

    pub fn position(&self) -> na::Point2<f32> {
        self.position
    }
}

• Мир? Есть.
• Животные? Есть.
• Еда? Есть.

Отлично.

Еще не хватает большого количества кода, но на данный момент его достаточно, чтобы отобразить что-нибудь на экране с помощью JS.

JS

Теперь вы можете спросить: "Если мы хотим вызывать это из JS, разве мы не должны везде использовать #[wasm_bindgen]?"

...на что я отвечу: "Отличный вопрос!"

Я думаю, важно помнить о разделении задач: в lib-simulation основное внимание должно уделяться тому, "как моделировать эволюцию", а не "как моделировать эволюцию и интегрироваться с WA".

Через секунду мы реализуем lib-simulation-wasm, и если мы оставим lib-simulation независимым от фронтенда, будет легко создать, скажем, lib-simulation-bevy или lib-simulation-cli - все они будут использовать общий код симуляции под капотом.

Хорошо, вернемся к lib-simulation-wasm. Нам нужно сообщить ему о rand и lib-simulation:

# libs/simulation-wasm/Cargo.toml

[dependencies]
rand = "0.8"
wasm-bindgen = "0.2"

lib-simulation = { path = "../simulation" }
                        # ^ путь является относительным к *этому* Cargo.toml

Теперь внутри lib-simulation-wasm мы можем обратиться к lib_simulation:

use lib_simulation as sim;

...и реализовать обертку для WA (это называется прокси):

use lib_simulation as sim;
use rand::prelude::*;
use wasm_bindgen::prelude::*;

#[wasm_bindgen]
pub struct Simulation {
    rng: ThreadRng,
    sim: sim::Simulation,
}

#[wasm_bindgen]
impl Simulation {
    #[wasm_bindgen(constructor)]
    pub fn new() -> Self {
        let mut rng = thread_rng();
        let sim = sim::Simulation::random(&mut rng);

        Self { rng, sim }
    }
}

Выглядит неплохо, попробуем скомпилировать этот код.

wasm-pack build

INFO]: Checking for the Wasm target...
[INFO]: Compiling to Wasm...

   Compiling getrandom v0.2.2

   error: target is not supported, for more information see:
          https://docs.rs/getrandom/#unsupported-targets
--> /home/pwy/.cargo/registry/src/...
3:9
    |
213 | /         compile_error!("target is not supported, for more information see: \\
214 | |                         https://docs.rs/getrandom/#unsupported-targets");
    | |_________________________________________________________________________^

error[E0433]: failed to resolve: use of undeclared crate or module `imp`
   --> /home/pwy/.cargo/registry/src/...
5:5
    |
235 |     imp::getrandom_inner(dest)
    |     ^^^ use of undeclared crate or module `imp`

Честно говоря, эта ошибка застала меня врасплох. К счастью, связанная страница довольно хорошо описывает проблему: rand зависит от getrandom, который поддерживает WA для браузера, но только когда его явно об этом просят:

# libs/simulation-wasm/Cargo.toml

[dependencies]
# ...
getrandom = { version = "0.2", features = ["js"] }

Компилируемся:

[INFO]: Checking for the Wasm target...
[INFO]: Compiling to Wasm...

warning: field is never read: `rng`
    ...

warning: field is never read: `sim`
    ...

warning: 2 warnings emitted

    Finished release [optimized] target(s) in 0.01s

[WARN]: origin crate has no README
[INFO]: Installing wasm-bindgen...
[INFO]: Optimizing wasm binaries with `wasm-opt`...
[INFO]: Optional fields missing from Cargo.toml: 'description',
        'repository', and 'license'. These are not necessary, but
         recommended
[INFO]: :-) Done in 0.63s
[INFO]: :-) Your wasm pkg is ready to publish at /home/pwy/Projects/...

На стороне JS мы теперь можем сделать следующее:

// www/index.js
import * as sim from "lib-simulation-wasm";

const simulation = new sim.Simulation();

Отлично, у нас есть готовый движок симуляции!

Однако это довольно тихий движок, потому что в настоящее время он просто рандомизирует некоторых животных и еду и замолкает. Чтобы было интереснее, передадим больше данных в JS.

Для этого нам понадобится еще несколько моделей, они будут как бы скопированы из lib-simulation, но с учетом WA:

// libs/simulation-wasm/src/lib.rs
/* ... */

#[wasm_bindgen]
pub struct Simulation {
    /* ... */
}

#[wasm_bindgen]
#[derive(Clone, Debug)]
pub struct World {
    pub animals: Vec<Animal>,
}

#[wasm_bindgen]
#[derive(Clone, Debug)]
pub struct Animal {
    pub x: f32,
    pub y: f32,
}
// ^ Эта модель меньше `lib_simulation::Animal`, поскольку
// | позиция птицы - это все, что нам нужно на данный момент
// | на стороне JS, другие поля нам пока не нужны.

/* ... */

...и 2 метода преобразования:

/* ... */

#[wasm_bindgen]
impl Simulation {
    /* ... */
}

/* ... */

impl From<&sim::World> for World {
    fn from(world: &sim::World) -> Self {
        let animals = world.animals().iter().map(Animal::from).collect();

        Self { animals }
    }
}

impl From<&sim::Animal> for Animal {
    fn from(animal: &sim::Animal) -> Self {
        Self {
            x: animal.position().x,
            y: animal.position().y,
        }
    }
}

Теперь мы можем добавить:

/* ... */

#[wasm_bindgen]
impl Simulation {
    /* ... */

    pub fn world(&self) -> World {
        World::from(self.sim.world())
    }
}

/* ... */

Выполняем wasm-pack build и...

error[E0277]: the trait bound `Vec<Animal>: std::marker::Copy` is not satisfied
  --> libs/simulation-wasm/src/lib.rs
   |
   |     pub animals: Vec<Animal>,
   |                            ^ the trait `std::marker::Copy` is not ...
   |

Это произошло, потому что #[wasm_bindgen] автоматически создает геттеры и сеттеры для JS, но требует, чтобы эти поля были Copy. Макрос делает нечто похожее на:

impl World {
    pub fn animals(&self) -> Vec<Animal> {
        self.animals
    }
}

...что тоже не будет работать без явного .clone() - это именно то, что нам нужно сообщить #[wasm_bindgen]:

/* ... */

#[wasm_bindgen]
#[derive(Clone, Debug)]
pub struct World {
    #[wasm_bindgen(getter_with_clone)]
    pub animals: Vec<Animal>,
}

/* ... */

// www/index.js
import * as sim from "lib-simulation-wasm";

const simulation = new sim.Simulation();
const world = simulation.world();

Все это должно работать...​ в теории, но как убедиться, что наш мир содержит какие-либо значимые данные? Используя наши собственные глаза!

Большинство браузеров предоставляют инструменты разработчика, доступ к которым можно получить, нажав F12.

Что мы можем сделать? Мы можем напечатать что-нибудь в консоли:

/* ... */

for (const animal of world.animals) {
  console.log(animal.x, animal.y);
}

Теперь, когда мы знаем положение животных, мы можем их нарисовать!

Привет, графика!

Рисовать в HTML + JS относительно легко - мы будем использовать вещь под названием canvas (холст):

<!DOCTYPE html>
<html>
  <head>
    <meta charset="utf-8">
    <title>Hello wasm-pack!</title>
  </head>

  <body>
    <canvas id="viewport"></canvas>
    <script src="./bootstrap.js"></script>
  </body>
</html>

У нашего холста есть атрибут id - этот атрибут используется для идентификации тегов, чтобы их можно было легко найти в JS:

/* ... */

const viewport = document.getElementById('viewport');
// ------------- ^------^
// | `document` - это глобальный объект, предоставляющий доступ и позволяющий модифицировать
// | текущую страницу (например, создавать и удалять элементы на ней).
// ---

Если вы хотите воспользоваться моментом, чтобы переварить происходящее, смело используйте console.log(viewport) и изучите свойства холста - их очень много!

Чтобы отобразить что-либо на canvas, нам нужно запросить определенный режим рисования (2D или 3D):

/* ... */

const ctxt = viewport.getContext('2d');

Для справки, наш ctxt имеет тип CanvasRenderingContext2D.

Существует большое количество методов и свойств, которые мы можем вызвать на ctxt. Начнем с fillStyle и fillRect():

/* ... */

// ---
// | Определяет цвет фигуры.
// - v-------v
ctxt.fillStyle = 'rgb(255, 0, 0)';
// ------------------ ^-^ -^ -^
// | Каждый из трех параметров - число от 0 до 255, включительно:
// |
// | rgb(0, 0, 0) = black
// |
// | rgb(255, 0, 0) = red
// | rgb(0, 255, 0) = green
// | rgb(0, 0, 255) = blue
// |
// | rgb(255, 255, 0) = yellow
// | rgb(0, 255, 255) = cyan
// | rgb(255, 0, 255) = magenta
// |
// | rgb(128, 128, 128) = gray
// | rgb(255, 255, 255) = white
// ---

ctxt.fillRect(10, 10, 100, 50);
// ---------- X   Y   W    H
// | Рисует прямоугольник, заполненный цветом, определенным с помощью `fillStyle`.
// |
// | X = координата по оси X (слева направо)
// | Y = координата по оси Y (сверху вниз)
// | W = ширина
// | X = высота
// |
// | (единица измерения - пиксель)
// ---

Запуск этого кода заставляет наш canvas нарисовать красный прямоугольник:

Ах, Мондриан был бы так горд - говорю вам: мы двигаемся в правильном направлении!

Система координат canvas:

Это мои данные

Теперь, когда мы знаем, как рисовать прямоугольники, используем наши данные:

import * as sim from "lib-simulation-wasm";

const simulation = new sim.Simulation();
const viewport = document.getElementById('viewport');
const ctxt = viewport.getContext('2d');

ctxt.fillStyle = 'rgb(0, 0, 0)';

for (const animal of simulation.world().animals) {
    ctxt.fillRect(animal.x, animal.y, 15, 15);
}

...и:

Что случилось? Изучим наши данные еще раз:

/* ... */

for (const animal of simulation.world().animals) {
  console.log(animal.x, animal.y);
}

0.6751065850257874 0.9448947906494141
0.2537931203842163 0.4474523663520813
0.7111597061157227 0.731094241142273
0.20178401470184326 0.5820554494857788
0.7062546610832214 0.3024316430091858
0.030273854732513428 0.4638679623603821
0.48392945528030396 0.9207395315170288
0.49439138174057007 0.24340438842773438
0.5087683200836182 0.10066533088684082
/* ... */

Позиции наших животных принадлежат диапазону <0.0, 1.0>, а canvas ожидает координаты в пикселях - мы можем это исправить, масштабируя числа во время рендеринга:

/* ... */

const viewport = document.getElementById('viewport');
const viewportWidth = viewport.width;
const viewportHeight = viewport.height;

/* ... */

for (const animal of simulation.world().animals) {
    ctxt.fillRect(
        animal.x * viewportWidth,
        animal.y * viewportHeight,
        15,
        15,
    );
}

...что дает нам:

Если вы являетесь счастливым обладателем дисплея HiDPI, то можете заметить, что холст выглядит немного размытым - не трогайте монитор, все "правильно".

Это связано с тем, что большинство, если не все, браузеры отображают холсты без корректировки плотности пикселей экрана, а затем искусственно повышают масштаб изображения, чтобы оно соответствовало фактическому разрешению экрана.

Преодоление этого "неудобства" требует некоторой хитрости, которая сводится к ручному увеличению размеров холста перед рисованием, чтобы "исправить" поведение браузера по умолчанию:

/* ... */

const viewportWidth = viewport.width;
const viewportHeight = viewport.height;

const viewportScale = window.devicePixelRatio || 1;
// ------------------------------------------ ^^^^
// | Это похоже на `.unwrap_or(1)`
// |
// | Это значение определяет количество физических пикселей
// | в одном пикселе на холсте.
// |
// | Не HiDPI дисплеи обычно имеют плотность пикселей, равную 1.0.
// | Это означает, что рисование одного пикселя на холсте раскрасит
// | ровно один физический пиксель на экране.
// |
// | Мой дисплей имеет плотность пикселей, равную 2.0.
// | Это означает, что каждому пикселю, нарисованному на холсте,
// | будет соответствовать два физических пикселя, модифицированных браузером.
// ---

// Трюк, часть 1: мы увеличиваем *буфер* холста, чтобы он
// совпадал с плотностью пикселей экрана
viewport.width = viewportWidth * viewportScale;
viewport.height = viewportHeight * viewportScale;

// Трюк, часть 2: мы уменьшаем *элемент* холста, поскольку
// браузер автоматически умножит его на плотность пикселей через мгновение.
//
// Это может показаться бесполезным, но суть заключается в том,
// что модификация размера элемента холста не влияет на
// размер его буфера, который *остается* увеличенным:
//
// ----------- < наша страница
// |         |
// |   ---   |
// |   | | < | < наш холст
// |   ---   |   (размер: viewport.style.width & viewport.style.height)
// |         |
// -----------
//
// За пределами страницы, в памяти браузера:
//
// ----- < буфер нашего холста
// |   | (размер: viewport.width & viewport.height)
// |   |
// -----
viewport.style.width = viewportWidth + 'px';
viewport.style.height = viewportHeight + 'px';

const ctxt = viewport.getContext('2d');

// Автоматически масштабирует все операции на `viewportScale`, иначе
// нам пришлось бы `* viewportScale` все вручную
ctxt.scale(viewportScale, viewportScale);

// Остальной код без изменений
ctxt.fillStyle = 'rgb(0, 0, 0)';

for (const animal of simulation.world().animals) {
    ctxt.fillRect(
        animal.x * viewportWidth,
        animal.y * viewportHeight,
        15,
        15,
    );
}

Это дает нам четкое изображение:

Верите или нет, но кто-то сказал мне, что квадратное уже не в моде!

Судя по всему, сейчас в моде ▼ треугольники ▲, попробуем нарисовать один.

К сожалению, JS не предоставляет метода для рисования треугольников, поэтому нам придется рисовать их вручную, вершина за вершиной.

Чтобы понять, как это работает, начнем с жестко закодированного примера:

/* ... */

// Начинаем рисовать многоугольник
ctxt.beginPath();

// Передвигаем курсор на x=50, y=0
ctxt.moveTo(50, 0);

// Рисуем линию от (50,0) до (100,50) и передвигаем курсор туда
// (это рисует правую сторону нашего треугольника)
ctxt.lineTo(100, 50);

// Рисуем линию от (100,50) до (0,50) и передвигаем курсор туда
// (это рисует нижнюю сторону)
ctxt.lineTo(0, 50);

// Рисуем линию от (0,50) до (50,0) и передвигаем курсор туда
// (это рисует левую сторону)
ctxt.lineTo(50, 0);

// Заливаем треугольник черным цветом
// (также существует `ctxt.stroke();`, который нарисует
// треугольник без заливки).
ctxt.fillStyle = 'rgb(0, 0, 0)';
ctxt.fill();

Какая красота!

Поскольку рисование треугольника требует нескольких шагов, создадим вспомогательную функцию:

/* ... */

function drawTriangle(ctxt, x, y, size) {
    ctxt.beginPath();
    ctxt.moveTo(x, y);
    ctxt.lineTo(x + size, y + size);
    ctxt.lineTo(x - size, y + size);
    ctxt.lineTo(x, y);

    ctxt.fillStyle = 'rgb(0, 0, 0)';
    ctxt.fill();
}

drawTriangle(ctxt, 50, 0, 50);

...или если быть более идиоматичным:

/* ... */

// ---
// | Тип (точнее, прототип) нашего `ctxt`.
// v------------------ v
CanvasRenderingContext2D.prototype.drawTriangle =
    function (x, y, size) {
        this.beginPath();
        this.moveTo(x, y);
        this.lineTo(x + size, y + size);
        this.lineTo(x - size, y + size);
        this.lineTo(x, y);

        this.fillStyle = 'rgb(0, 0, 0)';
        this.fill();
    };

ctxt.drawTriangle(50, 0, 50);

Прим. пер.: модификация прототипа объекта является антипаттерном в JS.

JS позволяет создавать методы во время выполнения, аналогичный код на Rust потребовал бы создания типажа:

trait DrawTriangle {
    fn draw_triangle(&mut self, x: f32, y: f32, size: f32);
}

impl DrawTriangle for CanvasRenderingContext2D {
    fn draw_triangle(&mut self, x: f32, y: f32, size: f32) {
        self.begin_path();
        /* ... */
    }
}

Теперь мы можем сделать так:

<!-- ... -->
<canvas id="viewport" width="800" height="800"></canvas>
<!-- ... -->

/* ... */

for (const animal of simulation.world().animals) {
    ctxt.drawTriangle(
        animal.x * viewportWidth,
        animal.y * viewportHeight,
        0.01 * viewportWidth,
    );
}

Если эти треугольники кажутся вам слишком маленькими, смело регулируйте размер холста и параметр 0.01.

Отлично 😎

...и знаете, что было бы еще лучше? Если бы треугольники были повернутыми!

Вершины

У нас уже есть поле rotation внутри lib-simulation:

/* ... */

#[derive(Debug)]
pub struct Animal {
    /* ... */
    rotation: na::Rotation2<f32>,
    /* ... */
}

...поэтому все, что нам нужно сделать, это передать его в JS:

/* ... */

#[wasm_bindgen]
#[derive(Clone, Debug)]
pub struct Animal {
    pub x: f32,
    pub y: f32,
    pub rotation: f32,
}

impl From<&sim::Animal> for Animal {
    fn from(animal: &sim::Animal) -> Self {
        Self {
            x: animal.position().x,
            y: animal.position().y,
            rotation: animal.rotation().angle(),
        }
    }
}

/* ... */

Выполняем wasm-pack build и возвращаемся к JS.

Поскольку вращение будет разным для каждого треугольника, нам понадобится еще один параметр:

/* ... */

CanvasRenderingContext2D.prototype.drawTriangle =
    function (x, y, size, rotation) {
        /* ... */
    };

/* ... */

Интуитивно мы ищем следующее:

...но обобщенное для любого угла.

Вершины (математика)

Вернемся к нашему треугольнику вместе с окружностью:

В данном случае я бы описал вращение как перемещение каждой вершины вдоль круга "под" определенным углом:

Как узнать, куда перемещать эти точки? Что ж, когда речь идет о круге, как правило, прибегают к тригонометрии.

Возможно, вы слышали о cos() и sin():

При их применении к кругу, можно заметить, что cos(angle) возвращает координату y точки, "повернутой" на определенный угол, а sin(angle) возвращает координату x:

Я использую кавычки вокруг вращения точки, потому что технически говорить о вращении точки не имеет смысла. Надеюсь, математики среди вас простят меня за этот добросовестный семантический грех.

На самом деле мы собираемся использовать x = -sin(angle), потому что nalgebra понимает вращение против часовой стрелки.

Если то, что у нас есть на данный момент:

this.moveTo(x, y);

...значит, вращение координаты x требует применения - sin():

this.moveTo(
    x - Math.sin(rotation) * size,
    y,
);

...а вращение координаты y требует применения + cos():

this.moveTo(
    x - Math.sin(rotation) * size,
    y + Math.cos(rotation) * size,
);

...где rotation измеряется в радианах, поэтому <0°, 360°> становится <0, 2 * PI>:

• 0° ⇒ rotation = 0
• 180° ⇒ rotation = PI
• 360° ⇒ rotation = 2 * PI
• 90° ⇒ 180° / 2 ⇒ rotation = PI / 2
• 45° ⇒ 180° / 4 ⇒ rotation = PI / 4
• и т.д.

Отлично, с одной вершиной разобрались:

...осталось еще две.

Поскольку весь круг занимает 360°, а нам нужно нарисовать три вершины, то каждая вершина будет занимать 360°/3 = 120°; учитывая, что первая вершина лежит на 0°, вторая вершина будет расположена на 120°.

Быстрый перевод в радианы с использованием пропорций:

{ 2 * PI = 360°
{      x = 120°

         ^
         |
         v

360° * x = 2 * PI * 120°    | делить на 2
180° * x = PI * 120°        | делить на 180°
       x = PI * 120° / 180° | упростить
       x = PI * 2 / 3       | переместить константу
       x = 2 / 3 * PI       | наслаждаться

...что дает нам:

this.moveTo(
    x - Math.sin(rotation) * size,
    y + Math.cos(rotation) * size,
);

this.lineTo(
    x - Math.sin(rotation + 2.0 / 3.0 * Math.PI) * size,
    y + Math.cos(rotation + 2.0 / 3.0 * Math.PI) * size,
);

Для третьей вершины:

2 * PI = 360°
     x = 120° + 120°

/* ... */

x = 4 / 3 * PI

...что дает нам:

this.moveTo(
    x - Math.sin(rotation) * size,
    y + Math.cos(rotation) * size,
);

this.lineTo(
    x - Math.sin(rotation + 2.0 / 3.0 * Math.PI) * size,
    y + Math.cos(rotation + 2.0 / 3.0 * Math.PI) * size,
);

this.lineTo(
    x - Math.sin(rotation + 4.0 / 3.0 * Math.PI) * size,
    y + Math.cos(rotation + 4.0 / 3.0 * Math.PI) * size,
);

Вместо + 4.0 / 3.0, мы можем использовать - 2.0 / 3.0 (60° против часовой стрелки от верхней вершины):

this.lineTo(
    x - Math.sin(rotation - 2.0 / 3.0 * Math.PI) * size,
    y + Math.cos(rotation - 2.0 / 3.0 * Math.PI) * size,
);

...результат будет одинаковым.

Нам не хватает последнего ребра, идущего из третьей вершины обратно в первую:

...поэтому:

/* ... */

this.lineTo(
    x - Math.sin(rotation + 4.0 / 3.0 * Math.PI) * size,
    y + Math.cos(rotation + 4.0 / 3.0 * Math.PI) * size,
);

this.lineTo(
    x - Math.sin(rotation) * size,
    y + Math.cos(rotation) * size,
);

Полный код:

/* ... */

CanvasRenderingContext2D.prototype.drawTriangle =
    function (x, y, size, rotation) {
        this.beginPath();

        this.moveTo(
            x - Math.sin(rotation) * size,
            y + Math.cos(rotation) * size,
        );

        this.lineTo(
            x - Math.sin(rotation + 2.0 / 3.0 * Math.PI) * size,
            y + Math.cos(rotation + 2.0 / 3.0 * Math.PI) * size,
        );

        this.lineTo(
            x - Math.sin(rotation + 4.0 / 3.0 * Math.PI) * size,
            y + Math.cos(rotation + 4.0 / 3.0 * Math.PI) * size,
        );

        this.lineTo(
            x - Math.sin(rotation) * size,
            y + Math.cos(rotation) * size,
        );

        this.stroke();
    };

ctxt.drawTriangle(50, 50, 25, Math.PI / 4);

Это работает?

...но сложно заметить, что треугольник повернут. Что, если мы вытянем одну из вершин?

/* ... */

CanvasRenderingContext2D.prototype.drawTriangle =
    function (x, y, size, rotation) {
        this.beginPath();

        this.moveTo(
            x - Math.sin(rotation) * size * 1.5,
            y + Math.cos(rotation) * size * 1.5,
        );

        /* ... */

        this.lineTo(
            x - Math.sin(rotation) * size * 1.5,
            y + Math.cos(rotation) * size * 1.5,
        );

        this.stroke();
    };

/* ... */

Так лучше:

Животные

Теперь мы можем модифицировать наш код:

/* ... */

for (const animal of simulation.world().animals) {
    ctxt.drawTriangle(
        animal.x * viewportWidth,
        animal.y * viewportHeight,
        0.01 * viewportWidth,
        animal.rotation,
    );
}

...что дает нам:

Замечательно!

Разработка: step()

Стационарные треугольники - это круто, но движущиеся треугольники круче.

У наших птиц нет мозга, но у них есть вращение и скорость. Это означает, что мы можем применять к ним физику, даже если они пока не могут взаимодействовать с окружающей средой:

/* ... */

impl Simulation {
    /* ... */

    /// Выполняет один шаг - одну секунду нашей симуляции, так сказать.
    pub fn step(&mut self) {
        for animal in &mut self.world.animals {
            animal.position += animal.rotation * animal.speed;
        }
    }
}

/* ... */

Выполняем cargo check:

error[E0277]: cannot multiply `Rotation<f32, 2_usize>` by `f32`
   |
   |             animal.position += animal.rotation * animal.speed;
   |                                                ^
   |             -----------------------------------|
   |             no implementation for `Rotation<f32, 2_usize> * f32`
   |
   = help: the trait `Mul<f32>` is not implemented for
     `Rotation<f32, 2_usize>`

Хм, nalgebra не поддерживает Rotation2 * f32. Возможно, мы можем использовать вектор?

animal.position += animal.rotation * na::Vector2::new(0.0, animal.speed);

cargo check

Finished dev [unoptimized + debuginfo] target(s) in 18.04s

Бинго!

Почему ::new(0.0, animal.speed)?

nalgebra не имеет точки отсчета, инструкция пожалуйста, переместись на 45° не содержит достаточно информации для вычисления того, куда должна переместиться птичка: 45° по какой оси?

Эту проблему решает наш ::new(0.0, animal.speed) - нас интересует вращение относительно оси Y, т.е. птица с поворотом 0° будет лететь вверх.

В общем, это довольно произвольное решение, которое полностью соответствует тому, как мы визуализируем треугольники на холсте; мы могли бы сделать, например, ::new(-animal.speed, 0.0) и настроить функцию drawTriangle() соответствующим образом.

Имея функцию step() внутри lib-simulation, мы можем предоставить ее через lib-simulation-wasm:

/* ... */

#[wasm_bindgen]
impl Simulation {
    /* ... */

    pub fn step(&mut self) {
        self.sim.step();
    }
}

/* ... */

Компилируем код:

wasm-pack build

....
[INFO]: :-) Done in 3.58s
[INFO]: :-) Your wasm pkg is ready to publish at /home/pwy/Projects/...

Что касается вызова .step() из JS, хотя в некоторых языках мы могли бы использовать цикл:

/* ... */

while (true) {
     ctxt.clearRect(0, 0, viewportWidth, viewportHeight);

     simulation.step();

     for (const animal of simulation.world().animals) {
         ctxt.drawTriangle(
             animal.x * viewportWidth,
             animal.y * viewportHeight,
             0.01 * viewportWidth,
             animal.rotation,
         );
     }
}

...среда веб-браузера немного усложняет задачу, поскольку наш код не должен быть блокирующим. Это связано с тем, что когда JS выполняется, браузер ждет его завершения, замораживая вкладку и не позволяя пользователю взаимодействовать со страницей.

Чем больше времени требуется для выполнения кода, тем дольше блокируется вкладка - по сути, она однопоточная. Итак, если мы напишем while (true) { ...​ }, браузер заблокирует вкладку навсегда, терпеливо ожидая, пока код завершит работу.

Вместо блокировки, можно использовать функцию под названием requestAnimationFrame() - она планирует выполнение функции непосредственно перед отрисовкой следующего кадра, а сама завершается немедленно:

/* ... */

function redraw() {
    ctxt.clearRect(0, 0, viewportWidth, viewportHeight);

    simulation.step();

    for (const animal of simulation.world().animals) {
        ctxt.drawTriangle(
            animal.x * viewportWidth,
            animal.y * viewportHeight,
            0.01 * viewportWidth,
            animal.rotation,
        );
    }

    // requestAnimationFrame() планирует выполнение кода перед отрисовкой следующего кадра.
    //
    // Поскольку мы хотим, чтобы наша симуляция выполнялась вечно,
    // функцию необходимо зациклить
    requestAnimationFrame(redraw);
}

redraw();

Вуаля:

...эм, почему птицы через некоторое время исчезают?

Вернемся к lib-simulation:

/* ... */

impl Simulation {
    /* ... */

    pub fn step(&mut self) {
        for animal in &mut self.world.animals {
            animal.position += animal.rotation * na::Vector2::new(0.0, animal.speed);
        }
    }
}

/* ... */

Итак, мы добавляем вращение к положению и... ах, да! Наша карта ограничена координатами <0.0, 1.0> - все, что находится за пределами этих координат, отображается за пределами холста.

Исправим это:

/* ... */

impl Simulation {
    /* ... */

    pub fn step(&mut self) {
        for animal in &mut self.world.animals {
            animal.position += animal.rotation * na::Vector2::new(0.0, animal.speed);

            animal.position.x = na::wrap(animal.position.x, 0.0, 1.0);
            animal.position.y = na::wrap(animal.position.y, 0.0, 1.0);
        }
    }
}

/* ... */

wrap() делает следующее: первый аргумент - это проверяемое число, а второй и третий аргументы определяют минимально и максимально допустимые значения:

• na::wrap(0.5, 0.0, 1.0) == 0.5 (числа между [min,max] остаются нетронутыми)
• na::wrap(-0.5, 0.0, 1.0) == 1.0 (if число < min { return max; })
• na::wrap(1.5, 0.0, 1.0) == 0.0 (if число > max { return min; })

wasm-pack build

Отлично!

Ты не ты (когда голоден)

Птицы составляют лишь половину нашей экосистемы, у нас еще есть еда.

Рендеринг еды

Поскольку мы уже написали много кода, рендеринг еды сводится к нескольким изменениям:

/* ... */

#[wasm_bindgen]
#[derive(Clone, Debug)]
pub struct World {
    #[wasm_bindgen(getter_with_clone)]
    pub animals: Vec<Animal>,

    #[wasm_bindgen(getter_with_clone)]
    pub foods: Vec<Food>,
}

impl From<&sim::World> for World {
    fn from(world: &sim::World) -> Self {
        let animals = world.animals().iter().map(Animal::from).collect();
        let foods = world.foods().iter().map(Food::from).collect();

        Self { animals, foods }
    }
}

/* ... */

#[wasm_bindgen]
#[derive(Clone, Debug)]
pub struct Food {
    pub x: f32,
    pub y: f32,
}

impl From<&sim::Food> for Food {
    fn from(food: &sim::Food) -> Self {
        Self {
            x: food.position().x,
            y: food.position().y,
        }
    }
}

/* ... */

CanvasRenderingContext2D.prototype.drawTriangle =
    function (x, y, size, rotation) {
        /* ... */
    };

CanvasRenderingContext2D.prototype.drawCircle =
    function(x, y, radius) {
        this.beginPath();

        // ---
        // | Центр круга.
        // ----- v -v
        this.arc(x, y, radius, 0, 2.0 * Math.PI);
        // ------------------- ^ -^-----------^
        // | Начало и конец окружности, в радианах.
        // |
        // | Меняя эти параметры можно, например, нарисовать
        // | только половину круга.
        // ---

        this.fillStyle = 'rgb(0, 0, 0)';
        this.fill();
    };

function redraw() {
    ctxt.clearRect(0, 0, viewportWidth, viewportHeight);

    simulation.step();

    const world = simulation.world();

    for (const food of world.foods) {
        ctxt.drawCircle(
            food.x * viewportWidth,
            food.y * viewportHeight,
            (0.01 / 2.0) * viewportWidth,
        );
    }

    for (const animal of world.animals) {
        /* ... */
    }

    /* ... */
}

/* ... */

Верите или нет, но этого достаточно!

wasm-pack build

....
[INFO]: :-) Done in 1.25s
[INFO]: :-) Your wasm pkg is ready to publish at /home/pwy/Projects/...

Наведение красоты

Наша математика работает, но внешний вид нашей симуляции... оставляет желать лучшего. Давайте это исправим:

<!DOCTYPE html>
<html>
  <head>
    <meta charset="utf-8">
    <title>Shorelark</title>
  </head>
  <style>
    body {
      background: #1f2639;
    }
  </style>
  <body>
    <canvas id="viewport" width="800" height="800"></canvas>
    <script src="./bootstrap.js"></script>
  </body>
</html>

/* ... */

CanvasRenderingContext2D.prototype.drawTriangle =
    function (x, y, size, rotation) {
        /* ... */

        this.fillStyle = 'rgb(255, 255, 255)';
        this.fill();
    };

CanvasRenderingContext2D.prototype.drawCircle =
    function(x, y, radius) {
        /* ... */

        this.fillStyle = 'rgb(0, 255, 128)';
        this.fill();
    };

/* ... */

Так лучше:

Симуляция еды

На данный момент, когда птички сталкиваются с едой, ничего не происходит - пора это пофиксить!

Сначала немного отрефакторим step():

/* ... */

impl Simulation {
    /* ... */

    pub fn step(&mut self) {
        self.process_movements();
    }

    fn process_movements(&mut self) {
        for animal in &mut self.world.animals {
            animal.position += animal.rotation * na::Vector2::new(0.0, animal.speed);

            animal.position.x = na::wrap(animal.position.x, 0.0, 1.0);
            animal.position.y = na::wrap(animal.position.y, 0.0, 1.0);
        }
    }
}

/* ... */

Теперь:

/* ... */

impl Simulation {
    /* ... */

    pub fn step(&mut self) {
        self.process_collisions();
        self.process_movements();
    }

    fn process_collisions(&mut self) {
        todo!();
    }

    /* ... */
}

/* ... */

Говоря простым языком, мы хотим достичь следующего:

/* ... */

fn process_collisions(&mut self) {
    for каждого животного {
        for каждой еды {
            if животное столкнулось с едой {
                обработка столкновения
            }
        }
    }
}

/* ... */

Проверка столкновения двух многоугольников называется тестированием на попадание (hit testing). Поскольку наши птицы представляют собой треугольники, а наша еда - круги, нам нужен какой-то "алгоритм проверки попадания треугольника в круг".

Но такой вид тестирования на попадание невероятно сложен, так что попробуем что-нибудь попроще, например: предположим, что наши птицы - круги.

Мы можем продолжать рисовать их в виде треугольников - дело в физике.

Итак, тестирование попадания "круг-круг" основано на проверке того, является ли расстояние между двумя кругами меньше или равным сумме их радиусов:

расстояние(A, B) > радиус(A) + радиус(B) ⇒ нет столкновения

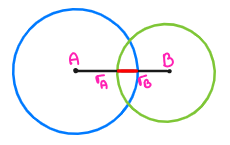
расстояние(A, B) <= радиус(A) + радиус(B) ⇒ столкновение

На практике это сводится к одному if:

// libs/simulation/src/lib.rs
/* ... */

pub fn step(&mut self, rng: &mut dyn RngCore) {
    self.process_collisions(rng);
    self.process_movements();
}

fn process_collisions(&mut self, rng: &mut dyn RngCore) {
    for animal in &mut self.world.animals {
        for food in &mut self.world.foods {
            let distance = na::distance(&animal.position, &food.position);

            if distance <= 0.01 {
                food.position = rng.gen();
            }
        }
    }
}

/* ... */

// libs/simulation-wasm/src/lib.rs
/* ... */

#[wasm_bindgen]
impl Simulation {
    /* ... */

    pub fn step(&mut self) {
        self.sim.step(&mut self.rng);
    }
}

/* ... */

Расстояние, возвращаемое nalgebra, выражается в тех же единицах, что и позиции, поэтому, например, расстояние 0.5 означает, что животное и еда находятся на расстоянии половины карты друг от друга, а 0.0 означает, что они находятся в одних и тех же координатах.

0.01 определяет радиус еды. Я выбрал 0.01, потому что кажется, что оно хорошо сочетается с размерами, которые мы используем для рисования.

Это работает? О боже!

Часть 4.2

Птичка и мозг

Наши птицы могут летать, но пока не могут взаимодействовать с окружающей средой. В этом разделе мы реализуем глаза, которые позволят нашим птицам видеть еду, и мозг, который позволит нашим птицам решать, куда они хотят лететь.

Рефакторинг

В libs/simulation/src/lib.rs много кода, отрефакторим его.

Хорошее правило - хранить структуры в отдельных файлах, поэтому:

// libs/simulation/src/lib.rs
mod animal;
mod food;
mod world;

pub use self::{animal::*, food::*, world::*};
use nalgebra as na;
use rand::{Rng, RngCore};

pub struct Simulation {
    /* ... */
}

impl Simulation {
    /* ... */
}

// libs/simulation/src/animal.rs
use crate::*;

#[derive(Debug)]
pub struct Animal {
    /* ... */
}

impl Animal {
    /* ... */
}

// libs/simulation/src/food.rs
use crate::*;

#[derive(Debug)]
pub struct Food {
    /* ... */
}

impl Food {
    /* ... */
}

// libs/simulation/src/world.rs
use crate::*;

#[derive(Debug)]
pub struct World {
    /* ... */
}

impl World {
    /* ... */
}

...и:

cargo check

error[E0616]: field `animals` of struct `world::World` is private
  --> libs/simulation/src/lib.rs
   |
   |         for animal in &mut self.world.animals {
   |                                       ^^^^^^^ private field

error[E0616]: field `foods` of struct `world::World` is private
  --> libs/simulation/src/lib.rs
   |
   |             for food in &mut self.world.foods {
   |                                         ^^^^^ private field

/* ... */

О нет, мы всего лишь перетасовали код - что случилось? Взглянем на проблемное место:

// libs/simulation/src/lib.rs
/* ... */

impl Simulation {
    /* ... */

    fn process_collisions(&mut self, rng: &mut dyn RngCore) {
        for animal in &mut self.world.animals {
            //                       ^------^

            for food in &mut self.world.foods {
                //                     ^----^

                /* ... */
            }
        }
    }
}

Раньше, когда все 4 структуры находились в одном файле, правила видимости Rust позволяли им получать доступ к частным полям друг друга. Теперь, когда наши структуры находятся в разных файлах, непубличные поля им больше недоступны.

Есть два способа решить эту проблему:

1. Мы можем предоставить изменяемые геттеры (mutable getters):

// libs/simulation/src/world.rs
impl World {
    pub(crate) fn animals_mut(&mut self) -> &mut [Animal] {
        &mut self.animals
    }

    pub(crate) fn foods_mut(&mut self) -> &mut [Food] {
        &mut self.foods
    }
}

// libs/simulation/src/lib.rs
impl Simulation {
    fn process_collisions(&mut self, rng: &mut dyn RngCore) {
        for animal in self.world.animals_mut() {
            for food in self.world.foods_mut() {
                /* ... */
            }
        }
    }
}

2. Мы можем изменить поля структуры World, чтобы они были публичными в пределах крейта (crate-public), а не частными:

#[derive(Debug)]
pub struct World {
    pub(crate) animals: Vec<Animal>,
    pub(crate) foods: Vec<Food>,
}

Все поля (или функции) с pub(crate) видны всему коду внутри данного крейта, поэтому pub(crate) animals означает, что весь код внутри lib-simulation будет иметь доступ к world.animals, а другие крейты нет.

Что касается разницы между обоими фрагментами, то она довольно незначительна:

1. Некоторым людям больше нравятся изменяемые геттеры, потому что они упрощают рефакторинг (например, мы можем переименовать поле с animals на birds, но сохранить fn animals_mut(), чтобы избежать внесения критических изменений).
2. Другим людям больше нравятся публичные в пределах крейта поля, поскольку они делают код короче (нет необходимости создавать дополнительные функции).

Для простоты мы применим второй подход:

// libs/simulation/src/animal.rs
/* ... */

#[derive(Debug)]
pub struct Animal {
    pub(crate) position: na::Point2<f32>,
    pub(crate) rotation: na::Rotation2<f32>,
    pub(crate) speed: f32,
}

/* ... */

// libs/simulation/src/food.rs
/* ... */

#[derive(Debug)]
pub struct Food {
    pub(crate) position: na::Point2<f32>,
}

/* ... */

// libs/simulation/src/world.rs
/* ... */

#[derive(Debug)]
pub struct World {
    pub(crate) animals: Vec<Animal>,
    pub(crate) foods: Vec<Food>,
}

/* ... */

cargo check

Checking lib-simulation v0.1.0
    Checking lib-simulation-wasm v0.1.0
    Finished dev [unoptimized + debuginfo] target(s) in 0.57s

Круто! Теперь мы готовы к реализации зрения.

Глаз птички

Прим. пер.: в оригинале раздел называется "eye of the birdie" (вероятно, обыгрывается "eye of the tiger").

Что такое глаз?

Биолог скажет, что глаз - это орган, обеспечивающий зрение; философская точка зрения может заключаться в том, что глаз - это зеркало души; а я? Я думаю, что глаз...

// libs/simulation/src/lib.rs
mod animal;
mod eye;
mod food;
mod world;

pub use self::{animal::*, eye::*, food::*, world::*};

...это структура!

// libs/simulation/src/eye.rs
use crate::*;

#[derive(Debug)]
pub struct Eye;

Однако, это не просто структура - она должна иметь одну конкретную функцию:

/* ... */

impl Eye {
    pub fn process_vision() -> Vec<f32> {
        todo!()
    }
}

Результатом этой функции является вектор чисел, где каждое число (каждая клетка (cell) глаза) говорит нам, насколько близко находится еда, соответствующая (по направлению) этой клетке глаза:

Такой глаз определяется несколькими параметрами:

use crate::*;
use std::f32::consts::*;

/// Как далеко может видеть глаз:
///
/// -----------------
/// |               |
/// |               |
/// |               |
/// |@      %      %|
/// |               |
/// |               |
/// |               |
/// -----------------
///
/// Если @ - это птичка, а % - еда, то FOV_RANGE, равный:
///
/// - 0.1 = 10% карты = птица не видит еду (по крайней мере, в данном случае)
/// - 0.5 = 50% карты = птица видит одну еду
/// - 1.0 = 100% карты = птица видит обе еды
const FOV_RANGE: f32 = 0.25;

/// Как широко глаз может видеть.
///
/// Если @> - это птичка (повернутая вправо), а . - площадь,
/// которую она видит, тогда FOV_ANGLE, равный:
///
/// - PI/2 = 90° =
///   -----------------
///   |             /.|
///   |           /...|
///   |         /.....|
///   |       @>......|
///   |         \.....|
///   |           \...|
///   |             \.|
///   -----------------
///
/// - PI = 180° =
///   -----------------
///   |       |.......|
///   |       |.......|
///   |       |.......|
///   |       @>......|
///   |       |.......|
///   |       |.......|
///   |       |.......|
///   -----------------
///
/// - 2 * PI = 360° =
///   -----------------
///   |...............|
///   |...............|
///   |...............|
///   |.......@>......|
///   |...............|
///   |...............|
///   |...............|
///   -----------------
///
/// Поле зрения (field of view) зависит как от FOV_RANGE, так и от FOV_ANGLE:
///
/// - FOV_RANGE=0.4, FOV_ANGLE=PI/2:
///   -----------------
///   |       @       |
///   |     /.v.\     |
///   |   /.......\   |
///   |   ---------   |
///   |               |
///   |               |
///   |               |
///   -----------------
///
/// - FOV_RANGE=0.5, FOV_ANGLE=2*PI:
///   -----------------
///   |               |
///   |      ---      |
///   |     /...\     |
///   |    |..@..|    |
///   |     \.../     |
///   |      ---      |
///   |               |
///   -----------------
const FOV_ANGLE: f32 = PI + FRAC_PI_4;

/// Сколько фоторецепторов в одном глазу.
///
/// Большее количество клеток означает более "четкое" зрение птицы, позволяющее
/// более точно локализовать еду. Недостатком является то,
/// что процесс эволюции будет занимать больше времени, или даже провалится из-за
/// невозможности найти решение.
///
/// Я нашел достаточными значения между 3~11. Глаза с более чем
/// ~20 фоторецепторами приводят к существенно худшим результатам.
const CELLS: usize = 9;

#[derive(Debug)]
pub struct Eye {
    fov_range: f32,
    fov_angle: f32,
    cells: usize,
}

impl Eye {
    // FOV_RANGE, FOV_ANGLE & CELLS - значения, которые мы будем использовать в процессе
    // симуляции, но для тестов нам пригодится возможность
    // ручного создания глаза
    fn new(fov_range: f32, fov_angle: f32, cells: usize) -> Self {
        assert!(fov_range > 0.0);
        assert!(fov_angle > 0.0);
        assert!(cells > 0);

        Self { fov_range, fov_angle, cells }
    }

    pub fn cells(&self) -> usize {
        self.cells
    }

    pub fn process_vision(
        &self,
        position: na::Point2<f32>,
        rotation: na::Rotation2<f32>,
        foods: &[Food],
    ) -> Vec<f32> {
        todo!()
    }
}

impl Default for Eye {
    fn default() -> Self {
        Self::new(FOV_RANGE, FOV_ANGLE, CELLS)
    }
}

Основная схема нашего алгоритма такова:

/* ... */

pub fn process_vision(/* ... */) -> Vec<f32> {
    let mut cells = vec![0.0; self.cells];

    for food in foods {
        if food внутри fov {
           cells[клетка, которая видит эту еду] += как близко находится еда;
        }
    }

    cells
}

/* ... */

Как проверить, что еда находится в нашем поле зрения? Должны быть выполнены два условия:

1. Расстояние между нами и едой не должно превышать FOV_RANGE:

/* ... */

for food in foods {
    let vec = food.position - position;
    // ^ Представляет *вектор* от еды до нас
    //
    // Если вы впервые слышите слово `вектор`,
    // вот его краткое определение:
    //
    // > Вектор - это объект, содержащий *магнитуду* (длину)
    // > и *направление*.
    //
    // Можно сказать, что вектор - это стрелка:
    //
    //   ---> - это вектор с magnitude=3 (если считать каждый дефис
    //         за "единицу пространства") и direction=0°
    //        (по крайней мере, по оси X)
    //
    //    |   - это вектор с magnitude=1 и direction=90°
    //    v   (по крайней мере, когда мы поворачиваемся по часовой стрелке)
    //
    // Наши векторы "еда-птичка" такие же:
    //
    // ---------
    // |       |  дает нам такой вектор:
    // |@     %|          <-----
    // |       |  (magnitude=5, direction=180°)
    // ---------
    //
    // ---------  дает нам такой вектор:
    // |   %   |           |
    // |       |           |
    // |   @   |           v
    // ---------  (magnitude=2, direction=90°)
    //
    // Не путайте это с `Vec` в Rust или `std::vector` в C++,
    // которые технически *являются* векторами, но в более
    // абстрактном смысле
    //
    // (https://stackoverflow.com/questions/581426/why-is-a-c-vector-called-a-vector).
    //
    // ---
    // | Причудливый способ сказать "длина вектора".
    // ----------- v----v
    let dist = vec.norm();

    if dist >= self.fov_range {
        continue;
    }
}

/* ... */

Угол между нами и едой не должен превышать FOV_ANGLE, а поскольку зрение птичек симметрично (они видят одинаковое количество "слева" и "справа", как и люди), он должен лежать в диапазоне <-FOV_ANGLE/2, +FOV_ANGLE/2>:

/* ... */

for food in foods {
    /* ... */

    // Возвращает направление вектора по отношению к оси Y, т.е.:
    //
    //    ^
    //    |  = 0° = 0
    //
    //   --> = 90° = -PI / 2
    //
    //    |  = 180° = -PI
    //    v
    //
    // (если вы имели дело с вращением раньше - это замаскированный atan2)
    let angle = na::Rotation2::rotation_between(
        &na::Vector2::y(),
        &vec,
    ).angle();

    // Поскольку птица *тоже* вращается, мы также должны включить ее вращение:
    let angle = angle - rotation.angle();

    // Вращение оборачивается (от -PI до PI), т.е.:
    //
    //   = угол 2*PI
    //   = угол PI    (поскольку 2*PI >= PI)
    //   = угол 0     (            PI >= PI)
    //                (              0 < PI)
    //
    //  угол 2*PI + PI/2
    //  = угол 1*PI + PI/2  (поскольку 2*PI + PI/2 >= PI)
    //  = угол PI/2         (            PI + PI/2 >= PI)
    //                      (                  PI/2 < PI)
    //
    //  угол -2.5*PI
    //  = угол -1.5*PI  (поскольку -2.5*PI <= -PI)
    //  = угол -0.5*PI  (          -1.5*PI <= -PI)
    //                  (           -0.5*PI > -PI)
    //
    // Интуитивно:
    //
    // - двойной оборот вокруг оси эквивалентен
    //   одному обороту или отсутствию вращения
    //
    // - поворот сначала на 90°, а затем на 360° эквивалентен
    //   повороту только на 90° (*или* на 270°, но в
    //   противоположном направлении).
    let angle = na::wrap(angle, -PI, PI);

    // Если текущий угол находится за пределами поля зрения птички,
    // переходим к следующей еде
    if angle < -self.fov_angle / 2.0 || angle > self.fov_angle / 2.0 {
        continue;
    }
}

/* ... */

Хорошо, мы исключили всю еду, находящуюся вне поля зрения птички, но для того, чтобы глаз работал, нам нужно еще кое-что:

cells[клетка, которая видит эту еду] += как близко находится еда;

Определить, какая конкретная клетка видит еду, немного сложно, но все сводится к тому, чтобы посмотреть на угол между едой и глазом - например, для глаза с тремя клетками и углом обзора 120°:

На поэтическом языке кода:

/* ... */

for food in foods {
    /* ... */

    // Делает угол *относительным* к полю зрения птички, т.е.:
    // преобразует его из <-FOV_ANGLE/2,+FOV_ANGLE/2> в <0,FOV_ANGLE>.
    //
    // После этой операции:
    // - угол 0° означает "начало FOV",
    // - угол self.fov_angle означает "конец FOV".
    let angle = angle + self.fov_angle / 2.0;

    // Поскольку теперь этот угол находится в диапазоне <0,FOV_ANGLE>,
    // путем деления на FOV_ANGLE мы преобразуем его в диапазон <0,1>.
    //
    // Значение, которое мы получаем, можно считать процентом, т.е.:
    //
    // - 0.2 = еду видит "20%-ая" клетка глаза
    //         (еда находится немного слева)
    //
    // - 0.5 = еду видит "50%-ая" клетка глаза
    //         (еда напротив птички)
    //
    // - 0.8 = еду видит "80%-ая" клетка глаза
    //         (еда немного справа)
    let cell = angle / self.fov_angle;

    // С клеткой в диапазоне <0,1>, умножая ее на количество клеток,
    // мы получаем диапазон <0,CELLS> - это соответствует настоящему
    // индексу клетки в массиве `cells`.
    //
    // Скажем, мы получили 8 клеток глаза:
    // - 0.2 * 8 = 20% * 8 = 1.6 ~= 1 = вторая клетка (индексация начинается с 0!)
    // - 0.5 * 8 = 50% * 8 = 4.0 ~= 4 = пятая клетка
    // - 0.8 * 8 = 80% * 8 = 6.4 ~= 6 = седьмая клетка
    let cell = cell * (self.cells as f32);

    // Наша клетка `cell` имеет тип `f32` - перед тем, как мы сможем использовать ее для
    // индексации массива, нам нужно преобразовать ее в `usize`.
    //
    // Мы также делаем `.min()` для покрытия экстремального крайнего случая: для
    // cell=1.0 (что соответствует еде, находящейся максимально справа
    // от нашей птички), мы получим `cell`, равную `cells.len()`,
    // что на один элемент *больше*, чем содержит массив `cells`
    // (его диапазон <0, cells.len()-1>).
    //
    // Честно говоря, я поймал это только благодаря модульным тестам,
    // которые мы скоро напишем, поэтому если вы находите мои объяснения
    // неудовлетворительными, удалите `.min()` позже и посмотрите,
    // какой тест упадет и почему
    let cell = (cell as usize).min(cells.len() - 1);
}

/* ... */

Теперь, когда мы знаем индекс ячейки, нанесем последний штрих:

/* ... */

for food in foods {
    /* ... */

    // Энергия обратно пропорциональна расстоянию между птичкой
    // и проверяемой едой; т.е. если энергия равна:
    //
    // - 0.0001 = еда едва находится в поле зрения (очень далеко)
    // - 1.0000 = еда прямо напротив птицы.
    //
    // Мы также можем смоделировать энергию в обратном порядке - "чем выше энергия,
    // тем дальше еда" - но это сделает процесс обучения немного сложнее.
    //
    // Как всегда, не стесняйтесь экспериментировать! Это далеко
    // не единственный способ реализовать глаза.
    let energy = (self.fov_range - dist) / self.fov_range;

    cells[cell] += energy;
}

/* ... */

Много математики! Как нам проверить, что это работает? Конечно, с помощью тестов 😊

Ничего, кроме тестов

Прим. пер.: в оригинале раздел называется "nothing but tests" (возможно, обыгрывается "nothing but true").

Первое препятствие заключается в том, что наше зрение требует множества параметров для вычисления:

• диапазон FOV (один f32)
• угол FOV (один f32)
• количество клеток (один usize)
• позиция (два f32)
• вращение (один f32)

Даже игнорируя количество клеток, которое мы можем жестко закодировать без особых потерь, это дает нам 5 различных настроек, которые влияют друг на друга, плюс нам также нужно указать расположение еды!

Второе препятствие заключается в том, что функция Eye::process_vision возвращает Vec<f32> - это одна из тех функций, которые принимают несколько сухих чисел и возвращают несколько сухих чисел; это не только немного скучно, но также затрудняет тестирование: действительно ли vec![0.0, 0.1, 0.7] является правильным ответом для x=0,2, y=0,5? Кто знает!

Что касается первого препятствия, я собираюсь использовать так называемые параметризованные тесты. С некоторой долей скептицизма, параметризованные тесты - это когда мы создаем функцию тестирования:

#[test]
fn some_test() {
    /* ... */
}

...и заставляем ее принимать один или несколько параметров:

// Это всего лишь пример на псевдо-Rust

#[test(x=10, y=20, z=30)]
#[test(x=50, y=50, z=50)]
#[test(x=0, y=0, z=0)]
fn some_test(x: f32, y: f32, z: usize) {
    /* ... */
}

Эта методология позволяет тестировать код более тщательно, чем при копировании mod { ...​ }, просто потому, что очень легко добавлять больше крайних случаев.

Rust не поддерживает параметризованные тесты - по крайней мере, в том виде, как показано выше - но существует несколько крейтов, предоставляющих этот функционал; мы будем использовать test-case:

# libs/simulation/Cargo.toml
# ...

[dev-dependencies]
test-case = "3.3.1"

...который имеет довольно простой синтаксис:

// libs/simulation/src/eye.rs
/* ... */

#[cfg(test)]
mod tests {
    use super::*;
    use test_case::test_case;

    #[test_case(1.0)]
    #[test_case(0.5)]
    #[test_case(0.1)]
    fn fov_ranges(fov_range: f32) {
        todo!()
    }
}

Это решает первую проблему, по крайней мере, для практических целей; хотя мы все равно не сможем охватить все случаи (помните, сколько чисел может закодировать f32?). Чем больше тестовых случаев, тем выше вероятность того, что код работает, как ожидается.

Что касается второго препятствия: что если вместо того, чтобы сравнивать векторы чисел, мы будем сравнивать графические представления того, что видит птица?

Не спать: даже если process_vision() возвращает что-то вроде vec![0.0, 0.5, 0.0], это не значит, что мы обязаны сравнивать такие значения в наших тестах! Если вместо векторов мы будем сравнивать, например, " * ", будет намного проще убедиться, что глаза работают правильно.

Итак:

/* ... */

#[cfg(test)]
mod tests {
    use super::*;
    use test_case::test_case;

    fn test(
        foods: Vec<Food>,
        fov_range: f32,
        fov_angle: f32,
        x: f32,
        y: f32,
        rot: f32,
        expected_vision: &str,
    ) {
        todo!()
    }

    #[test_case(1.0)]
    #[test_case(0.5)]
    #[test_case(0.1)]
    fn fov_ranges(fov_range: f32) {
        super::test(
            todo!(),
            fov_range,
            todo!(),
            todo!(),
            todo!(),
            todo!(),
            todo!(),
         );
    }
}

Хм, слишком много параметров для одной функции... Как насчет структуры?

/* ... */

#[cfg(test)]
mod tests {
    use super::*;
    use test_case::test_case;

    struct TestCase {
        foods: Vec<Food>,
        fov_range: f32,
        fov_angle: f32,
        x: f32,
        y: f32,
        rot: f32,
        expected_vision: &'static str,
    }

    impl TestCase {
        fn run(self) {
            todo!()
        }
    }

    #[test_case(1.0)]
    #[test_case(0.5)]
    #[test_case(0.1)]
    fn fov_ranges(fov_range: f32) {
        TestCase {
            foods: todo!(),
            fov_angle: todo!(),
            x: todo!(),
            y: todo!(),
            rot: todo!(),
            expected_vision: todo!(),
            fov_range,
        }.run()
    }
}

Красиво и читабельно.

Результат теста, expected_vision, зависит от fov_range:

/* ... */

#[test_case(1.0, "пока непонятно")]
#[test_case(0.5, "пока непонятно")]
#[test_case(0.1, "пока непонятно")]
fn fov_ranges(fov_range: f32, expected_vision: &'static str) {
    TestCase {
        foods: todo!(),
        fov_angle: todo!(),
        x: todo!(),
        y: todo!(),
        rot: todo!(),
        fov_range,
        expected_vision,
    }.run()
}

/* ... */

Что касается этого TestCase, с высоты птичьего полета мы ищем следующее:

/* ... */

impl TestCase {
    fn run(self) {
        let eye = Eye::new(/* ... */);

        let actual_vision = eye.process_vision(/* ... */);
        let actual_vision = make_human_readable(actual_vision);

        assert_eq!(actual_vision, self.expected_vision);
    }
}

/* ... */

Приступаем к реализации TestCase:

/* ... */

/// Во всех наших тестах будут использоваться глаза, состоящие из 13 клеток.
///
/// Отвечая на "почему?":
///
/// Хотя мы определенно *можем* написать тесты для разного количества
/// клеток глаза, после некоторого размышления я пришел к выводу, что игра
/// не стоит свеч - как вы скоро увидите, мы итак получим хорошее покрытие
/// с помощью других параметров, поэтому создание отдельного набора тестов для
/// разных значений клеток глаза кажется пустой тратой времени.
///
/// Отвечая на "почему 13?":
///
/// Я проверил несколько чисел и обнаружил, что 13 дает
/// довольно хорошие результаты, вот и все.
const TEST_EYE_CELLS: usize = 13;

impl TestCase {
    fn run(self) {
        let eye = Eye::new(self.fov_range, self.fov_angle, TEST_EYE_CELLS);

        let actual_vision = eye.process_vision(
            na::Point2::new(self.x, self.y),
            na::Rotation2::new(self.rot),
            &self.foods,
        );
    }
}

/* ... */

В настоящее время actual_vision - это Vec<f32> - мы можем преобразовать его в строку с помощью магии into_iter(), map() и join():

/* ... */

impl TestCase {
    fn run(self) {
        /* ... */

        let actual_vision: Vec<_> = actual_vision
            .into_iter()
            .map(|cell| {
                // В качестве напоминания - чем выше значение клетки,
                // тем ближе еда:

                if cell >= 0.7 {
                    // <0.7, 1.0>
                    // еда прямо напротив
                    "#"
                } else if cell >= 0.3 {
                    // <0.3, 0.7)
                    // еда где-то дальше
                    "+"
                } else if cell > 0.0 {
                    // <0.0, 0.3)
                    // еда очень далеко
                    "."
                } else {
                    // 0.0
                    // в поле зрения нет еды, клетка видит пустое пространство
                    " "
                }
            })
            .collect();

        // Значения клеток (`0.7`, `0.3`, `0.0`) или символы (`#`, `+`, `.`)
        // не имеют никакого специального значения.

        // `join()` преобразует `Vec<String>` в `String` с помощью
        // разделителя - например, `vec!["a", "b", "c"].join("|")`
        // вернет `a|b|c`.
        let actual_vision = actual_vision.join("");

        assert_eq!(actual_vision, self.expected_vision);
    }
}

/* ... */

Наша система тестирования завершена! 🥳

Что касается тестов, позвольте представить вам чистую красоту:

/* ... */

fn food(x: f32, y: f32) -> Food {
    Food {
        position: na::Point2::new(x, y),
    }
}

/// В тестах этого модуля мы используем мир, который выглядит так:
///
/// -------------
/// |           |
/// |           |
/// |     @     |
/// |     v     | `v` показывает, куда смотрит птичка
/// |           |
/// |     %     |
/// -------------
///
/// Каждый тест последовательно уменьшает поле зрение птички и
/// проверяет, что она видит:
///
/// -------------
/// |           |
/// |           |
/// |     @     |
/// |    /v\    |
/// |  /.....\  | `.` показывает часть поля, которую видит птичка
/// |/....%....\|
/// -------------
///
/// -------------
/// |           |
/// |           |
/// |     @     |
/// |    /v\    |
/// |  /.....\  |
/// |     %     |
/// -------------
///
/// -------------
/// |           |
/// |           |
/// |     @     |
/// |    /.\    |
/// |           |
/// |     %     |
/// -------------
///
/// С течением времени мы видим, как еда постепенно исчезает в пустоте:
///
/// (технически, еда и птица не двигаются -
/// просто уменьшается поле зрение птички)
#[test_case(1.0, "      +      ")] // Еда внутри FOV
#[test_case(0.9, "      +      ")] // аналогично
#[test_case(0.8, "      +      ")] // аналогично
#[test_case(0.7, "      .      ")] // Еда медленно исчезает
#[test_case(0.6, "      .      ")] // аналогично
#[test_case(0.5, "             ")] // Еда исчезла!
#[test_case(0.4, "             ")]
#[test_case(0.3, "             ")]
#[test_case(0.2, "             ")]
#[test_case(0.1, "             ")]
fn fov_ranges(fov_range: f32, expected_vision: &'static str) {
    TestCase {
        foods: vec![food(0.5, 1.0)],
        fov_angle: FRAC_PI_2,
        x: 0.5,
        y: 0.5,
        rot: 0.0,
        fov_range,
        expected_vision,
    }.run()
}

/* ... */

Вдох-выдох:

cargo test -p lib-simulation

running 10 tests
test eye::tests::fov_ranges::_0_4_ ... ok
test eye::tests::fov_ranges::_0_2_ ... ok
test eye::tests::fov_ranges::_0_5_ ... ok
test eye::tests::fov_ranges::_0_1_ ... ok
test eye::tests::fov_ranges::_0_3_ ... ok
test eye::tests::fov_ranges::_0_8_ ... ok
test eye::tests::fov_ranges::_0_9_ ... ok
test eye::tests::fov_ranges::_1_0_ ... ok
test eye::tests::fov_ranges::_0_7_ ... ok
test eye::tests::fov_ranges::_0_6_ ... ok

test result: ok. 10 passed; 0 failed

Оно работает! И оно читабельно! И, если повезет, его даже можно будет поддерживать!

Код, который вы видите, уже содержит правильные значения для expected_vision, но на самом деле я не знал их заранее - за кулисами я сделал следующее:

#[test_case(1.0, "")]
/* ... */

...затем я запустил cargo test и скопировал фактический результат из сообщения об ошибке, анализируя его на предмет ошибки (например, получение # для fov_range, равного 0.1, может указывать на ошибку, так как птичка с таким маленький fov_range не должна видеть эту еду).

С одним параметром разобрались, осталось еще четыре. Что насчет вращения?

/* ... */

/// Мир:
///
/// -------------
/// |           |
/// |           |
/// |%    @     |
/// |     v     |
/// |           |
/// -------------
///
/// Тесты:
///
/// -------------
/// |...........|
/// |...........|
/// |%....@.....|
/// |.....v.....|
/// |...........|
/// -------------
///
/// -------------
/// |...........|
/// |...........|
/// |%...<@.....|
/// |...........|
/// |...........|
/// -------------
///
/// -------------
/// |...........|
/// |.....^.....|
/// |%....@.....|
/// |...........|
/// |...........|
/// -------------
///
/// -------------
/// |...........|
/// |...........|
/// |%....@>....|
/// |...........|
/// |...........|
/// -------------
///
/// ...продолжаем, пока не сделаем полный круг - поворот на 360°:
#[test_case(0.00 * PI, "         +   ")] // Еда справа
#[test_case(0.25 * PI, "        +    ")]
#[test_case(0.50 * PI, "      +      ")] // Еда напротив
#[test_case(0.75 * PI, "    +        ")]
#[test_case(1.00 * PI, "   +         ")] // Еда слева
#[test_case(1.25 * PI, " +           ")]
#[test_case(1.50 * PI, "            +")] // Еда позади
#[test_case(1.75 * PI, "           + ")] // (продолжаем до
#[test_case(2.00 * PI, "         +   ")] // fov_angle=360°.)
#[test_case(2.25 * PI, "        +    ")]
#[test_case(2.50 * PI, "      +      ")]
fn rotations(rot: f32, expected_vision: &'static str) {
    TestCase {
        foods: vec![food(0.0, 0.5)],
        fov_range: 1.0,
        fov_angle: 2.0 * PI,
        x: 0.5,
        y: 0.5,
        rot,
        expected_vision,
    }.run()
}

/* ... */

Тестирование позиций еще забавнее:

/* ... */

/// Мир:
///
/// ------------
/// |          |
/// |         %|
/// |          |
/// |         %|
/// |          |
/// ------------
///
/// Тесты для оси X:
///
/// ------------
/// |          |
/// |        /%|
/// |       @>.|
/// |        \%|
/// |          |
/// ------------
///
/// ------------
/// |        /.|
/// |      /..%|
/// |     @>...|
/// |      \..%|
/// |        \.|
/// ------------
///
/// ...продолжаем двигаться влево
///    (или, с точки зрения птицы, _назад_)
///
/// Тесты для оси Y:
///
/// ------------
/// |     @>...|
/// |       \.%|
/// |        \.|
/// |         %|
/// |          |
/// ------------
///
/// ------------
/// |      /...|
/// |     @>..%|
/// |      \...|
/// |        \%|
/// |          |
/// ------------
///
/// ...продолжаем двигаться вниз
///    (или, с точки зрения птицы, _вправо_)

// Проверяем ось X:
// (птица "улетает" от еды)
#[test_case(0.9, 0.5, "#           #")]
#[test_case(0.8, 0.5, "  #       #  ")]
#[test_case(0.7, 0.5, "   +     +   ")]
#[test_case(0.6, 0.5, "    +   +    ")]
#[test_case(0.5, 0.5, "    +   +    ")]
#[test_case(0.4, 0.5, "     + +     ")]
#[test_case(0.3, 0.5, "     . .     ")]
#[test_case(0.2, 0.5, "     . .     ")]
#[test_case(0.1, 0.5, "     . .     ")]
#[test_case(0.0, 0.5, "             ")]
//
// Проверяем ось Y:
// (птица "летит рядом" с едой)
#[test_case(0.5, 0.0, "            +")]
#[test_case(0.5, 0.1, "          + .")]
#[test_case(0.5, 0.2, "         +  +")]
#[test_case(0.5, 0.3, "        + +  ")]
#[test_case(0.5, 0.4, "      +  +   ")]
#[test_case(0.5, 0.6, "   +  +      ")]
#[test_case(0.5, 0.7, "  + +        ")]
#[test_case(0.5, 0.8, "+  +         ")]
#[test_case(0.5, 0.9, ". +          ")]
#[test_case(0.5, 1.0, "+            ")]
fn positions(x: f32, y: f32, expected_vision: &'static str) {
    TestCase {
        foods: vec![food(1.0, 0.4), food(1.0, 0.6)],
        fov_range: 1.0,
        fov_angle: FRAC_PI_2,
        rot: 3.0 * FRAC_PI_2,
        x,
        y,
        expected_vision,
    }.run()
}

/* ... */

Остался один параметр - угол поля зрения.

Мы будем использовать ту же систему, но представить, что здесь происходит, немного сложнее (по крайней мере, мне потребовалась минута, чтобы убедиться в правильности тестов):

/* ... */

/// Мир:
///
/// ------------
/// |%        %|
/// |          |
/// |%        %|
/// |    @>    |
/// |%        %|
/// |          |
/// |%        %|
/// ------------
///
/// Тесты:
///
/// ------------
/// |%        %|
/// |         /|
/// |%      /.%|
/// |    @>....|
/// |%      \.%|
/// |         \|
/// |%        %|
/// ------------
///
/// ------------
/// |%      /.%|
/// |      /...|
/// |%    /...%|
/// |    @>....|
/// |%    \...%|
/// |      \...|
/// |%      \.%|
/// ------------
///
/// ------------
/// |%........%|
/// |\.........|
/// |% \......%|
/// |    @>....|
/// |% /......%|
/// |/.........|
/// |%........%|
/// ------------
///
/// ...продолжаем, пока не достигнем FOV=360°
#[test_case(0.25 * PI, " +         + ")] // FOV узкое = 2 еды
#[test_case(0.50 * PI, ".  +     +  .")]
#[test_case(0.75 * PI, "  . +   + .  ")] // FOV становится
#[test_case(1.00 * PI, "   . + + .   ")] // шире и шире...
#[test_case(1.25 * PI, "   . + + .   ")]
#[test_case(1.50 * PI, ".   .+ +.   .")]
#[test_case(1.75 * PI, ".   .+ +.   .")]
#[test_case(2.00 * PI, "+.  .+ +.  .+")] // FOV широчайшее = 8 еды
fn fov_angles(fov_angle: f32, expected_vision: &'static str) {
    TestCase {
        foods: vec![
            food(0.0, 0.0),
            food(0.0, 0.33),
            food(0.0, 0.66),
            food(0.0, 1.0),
            food(1.0, 0.0),
            food(1.0, 0.33),
            food(1.0, 0.66),
            food(1.0, 1.0),
        ],
        fov_range: 1.0,
        x: 0.5,
        y: 0.5,
        rot: 3.0 * FRAC_PI_2,
        fov_angle,
        expected_vision,
    }.run()
}

/* ... */

Отлично:

cargo test -p lib-simulation

test result: ok. 49 passed; 0 failed

Итак, у нас есть глаза, а как насчет мозгов? К счастью, они у нас уже имеются!

// libs/simulation/Cargo.toml
# ...

[dependencies]
# ...

lib-neural-network = { path = "../neural-network" }

# ...

// libs/simuation/src/lib.rs
/* ... */

use lib_neural_network as nn;
use nalgebra as na;
use rand::{Rng, RngCore};

/* ... */

// libs/simulation/src/animal.rs
/* ... */

#[derive(Debug)]
pub struct Animal {
    /* ... */
    pub(crate) eye: Eye,
    pub(crate) brain: nn::Network,
}

impl Animal {
    pub fn random(rng: &mut dyn RngCore) -> Self {
        /* ... */

        let eye = Eye::default();

        let brain = nn::Network::random(
            rng,
            &[
                // Входной слой
                //
                // Поскольку зрение возвращает Vec<f32>, и нейронная
                // сеть работает с Vec<f32>, мы можем передавать
                // числа из глаз в сеть напрямую.
                //
                // Имей птички уши, например, мы могли бы
                // делать так: `eye.cells() + ear.nerves()` и т.д.
                nn::LayerTopology {
                    neurons: eye.cells(),
                },

                // Скрытый слой
                //
                // Лучшего ответа на "сколько нейронов
                // должен содержать скрытый слой?"
                // (или "сколько должно быть скрытых слоев?") не существует.
                //
                // Общее правило таково: начинаем с одного скрытого слоя,
                // содержащего немного больше нейронов, чем входной слой,
                // и смотрим, насколько хорошо работает сеть.
                nn::LayerTopology {
                    neurons: 2 * eye.cells(),
                },

                // Выходной слой
                //
                // Поскольку мозг будет управлять скоростью и вращением
                // птицы, нам требуется 2 числа = 2 нейрона.
                nn::LayerTopology { neurons: 2 },
            ],
        );

        Self {
            /* ... */
            eye,
            brain,
        }
    }

    /* ... */
}

// libs/simulation/src/lib.rs
/* ... */

// FRAC_PI_2 = PI / 2.0; удобное сокращение
use std::f32::consts::FRAC_PI_2;

/// Минимальная скорость птицы.
///
/// Сохранение скорости выше нуля позволяет избежать застревания птицы на одном месте.
const SPEED_MIN: f32 = 0.001;

/// Максимальная скорость птицы.
///
/// Ограничение скорости позволяет предотвратить разгон птицы до бесконечности,
/// что сделало бы симуляцию... нереалистичной :-)
const SPEED_MAX: f32 = 0.005;

/// Ускорение; определяет, насколько мозг может увеличивать
/// скорость птицы за один шаг.
///
/// Предположим, птица летит с speed=0.5, и мозг отдает команду
/// "остановиться", SPEED_ACCEL, равное:
///
/// - 0.1 = для замедления до SPEED_MIN птице потребуется 5 шагов ("5 секунд")
/// - 0.5 = для замедления до SPEED_MIN птице потребуется 1 шаг
///
/// Это делает симуляцию более реалистичной, поскольку, как и в реальной жизни,
/// невозможно мгновенно увеличить скорость с 1 км/ч до 50 км/ч,
/// даже если ваш мозг очень этого хочет.
const SPEED_ACCEL: f32 = 0.2;

/// Тоже самое, но для вращения:
///
/// - 2 * PI = для вращения на 360° птице потребуется 1 шаг
/// - PI = для вращения на 360° птице потребуется 2 шага
///
/// Я выбрал PI/2, потому что это значение показало себя лучше всего.
const ROTATION_ACCEL: f32 = FRAC_PI_2;

impl Simulation {
    /* ... */

    pub fn step(&mut self, rng: &mut dyn RngCore) {
        self.process_collisions(rng);
        self.process_brains();
        self.process_movements();
    }

    /* ... */

    fn process_brains(&mut self) {
        for animal in &mut self.world.animals {
            let vision = animal.eye.process_vision(
                animal.position,
                animal.rotation,
                &self.world.foods,
            );

            let response = animal.brain.propagate(vision);

            // ---
            // Ограничивает число определенным диапазоном.
            // -------------------- v---v
            let speed = response[0].clamp(-SPEED_ACCEL, SPEED_ACCEL);
            let rotation = response[1].clamp(-ROTATION_ACCEL, ROTATION_ACCEL);

            // Наши скорость & вращение здесь являются *относительными*, т.е. когда
            // они равны нулю, мозг говорит "продолжай лететь,
            // как летела", а не "перестань лететь".
            //
            // Критически важно, чтобы оба значения были относительными, поскольку мозг
            // не знает собственную скорость и вращение, поэтому
            // он в принципе не может возвращать абсолютные значения.

            animal.speed = (animal.speed + speed).clamp(SPEED_MIN, SPEED_MAX);
            animal.rotation = na::Rotation2::new(animal.rotation.angle() + rotation);

            // (нам не нужны ROTATION_MIN или ROTATION_MAX,
            // поскольку вращение после 2*PI автоматически возвращается к 0 -
            // мы уже наблюдали это, когда тестировали глаза
            // в `fn rotations { ... }`)
        }
    }

    /* ... */
}

Это работает? Давайте выясним!

wasm-pack build

...
[INFO]: :-) Done in 12.20s
[INFO]: :-) Your wasm pkg is ready to publish at /home/pwy/Projects/...

Это впечатляет: каждая птица, оснащенная рандомизированным мозгом, решает, куда она хочет лететь, пытаясь приспособиться к окружающей среде.

Некоторые птицы летают кругами, некоторые демонстрируют более сложное поведение - и, если вам повезет (попробуйте обновить страницу несколько раз!), вы увидите, что птица направляется к еде, как будто понимает, что делает.

Однако в настоящее время это вопрос удачи. Наша следующая и последняя веха будет связана с обучением - мы дополним нашу симуляцию последней частью головоломки: генетическим алгоритмом.

Ученье - свет

Хотя наши птицы умеют летать, их мозг остается полностью произвольным. В этом разделе мы интегрируем симуляцию с генетическим алгоритмом, чтобы птички могли учиться и развиваться.

Грубо говоря, мы хотим максимизировать количество съеденной пищи - это и будет нашей фитнес-функцией. Мы запустим симуляцию на некоторое время (так называемое поколение), запишем, сколько еды съела каждая птица, и затем размножим лучших птичек.

Сделаем это!

# libs/simulation/Cargo.toml
# ...

[dependencies]
# ...

lib-genetic-algorithm = { path = "../genetic-algorithm" }
lib-neural-network = { path = "../neural-network" }

# ...

// libs/simulation/src/lib.rs
/* ... */

use lib_genetic_algorithm as ga;
use lib_neural_network as nn;
/* ... */

// libs/simulation/src/lib.rs
/* ... */

/// Сколько `step()` должно произойти перед помещением данных в
/// генетический алгоритм?
///
/// Слишком низкое значение может помешать обучению птиц,
/// слишком высокое значение приведет к ненужному замедлению эволюции.
///
/// Это число может расцениваться как "количество шагов, в течение которых живет каждая птица".
/// 2500 было выбрано экспериментальным путем.
const GENERATION_LENGTH: usize = 2500;

pub struct Simulation {
    world: World,
    ga: ga::GeneticAlgorithm<ga::RouletteWheelSelection>,
    age: usize,
}

impl Simulation {
    pub fn random(rng: &mut dyn RngCore) -> Self {
        let world = World::random(rng);

        let ga = ga::GeneticAlgorithm::new(
            ga::RouletteWheelSelection,
            ga::UniformCrossover,
            ga::GaussianMutation::new(0.01, 0.3),
            // ---------------------- ^--^ -^-^
            // | Эти значения выбраны экспериментальным путем.
            // |
            // | Более высокие значения могут сделать симуляцию более хаотичной,
            // | что - немного контринтуитивно - может помочь ей
            // | обнаружить *лучшие* решения; недостатком является то,
            // | что более высокие значения могут привести к отбрасыванию
            // | хороших решений.
            // ---
        );

        Self { world, ga, age: 0 }
    }

    /* ... */

    pub fn step(&mut self, rng: &mut dyn RngCore) {
        self.process_collisions(rng);
        self.process_brains();
        self.process_movements();

        self.age += 1;

        if self.age > GENERATION_LENGTH {
            self.evolve(rng);
        }
    }

    /* ... */

    fn evolve(&mut self, rng: &mut dyn RngCore) {
        self.age = 0;

        // Шаг 1: готовим птичек к отправке в генетический алгоритм
        let current_population = todo!();

        // Шаг 2: эволюционируем птичек
        let evolved_population = self.ga.evolve(rng, &current_population);

        // Шаг 3: получаем птичек из генетического алгоритма
        self.world.animals = todo!();

        // Шаг 4: перезапускаем еду
        // (это не обязательно, но позволяет визуализировать
        // эволюцию с помощью UI)
        for food in &mut self.world.foods {
            food.position = rng.gen();
        }
    }
}

Как вы, возможно, помните, метод GeneticAlgorithm::evolve требует, чтобы "эволюционируемый" тип реализовал типаж Individual:

// libs/genetic-algorithm/src/lib.rs
impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(&self, rng: &mut dyn RngCore, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */
    }
}

...наивным подходом может быть реализация Individual для Animal - в конце концов, птички - это то, что мы хотим развивать:

// libs/simulation/src/animal.rs
/* ... */

impl ga::Individual for Animal {
    fn create(chromosome: ga::Chromosome) -> Self {
        todo!()
    }

    fn chromosome(&self) -> &ga::Chromosome {
        todo!()
    }

    fn fitness(&self) -> f32 {
        todo!()
    }
}

Но как только мы попытаемся это сделать, то поймем, что ничего не получится, например: как мы можем реализовать fn chromosome(), которая возвращает ссылку на ga::Chromosome, если Animal не содержит поля chromosome?

impl ga::Individual for Animal {
    /* ... */

    fn chromosome(&self) -> &ga::Chromosome {
       &self.what // :'-(
    }

    /* ... */
}

Конечно, вы можете сказать, что, поскольку мы контролируем код lib-genetic-algorithm, то можем просто изменить функцию chromosome, чтобы она работала с собственными Chromosome, и вы будете правы, частично! На самом деле это не решает основную проблему дизайна, а просто перемещает ее в другое место:

/* ... */

impl ga::Individual for Animal {
    fn create(chromosome: ga::Chromosome) -> Self {
        Self {
            position: rng.gen(), // ошибка: здесь мы не имеем доступа к ГПСЧ!
            /* ... */
        }
    }

    /* ... */
}

Предположим, что наш ga::Individual спроектирован верно, как тогда мы можем интегрировать с ним Animal?

Проще всего создать специальную структуру:

// libs/simulation/src/lib.rs
/* ... */

mod animal;
mod animal_individual;
/* ... */

use self::animal_individual::*;
use lib_genetic_algorithm as ga;
use lib_neural_network as nn;
/* ... */

// libs/simulation/src/animal_individual.rs
use crate::*;

pub struct AnimalIndividual;

impl ga::Individual for AnimalIndividual {
    fn create(chromosome: ga::Chromosome) -> Self {
        todo!()
    }

    fn chromosome(&self) -> &ga::Chromosome {
        todo!()
    }

    fn fitness(&self) -> f32 {
        todo!()
    }
}

Эта структура должна содержать как минимум два поля:

use crate::*;

pub struct AnimalIndividual {
    fitness: f32,
    chromosome: ga::Chromosome,
}

impl ga::Individual for AnimalIndividual {
    fn create(chromosome: ga::Chromosome) -> Self {
        Self {
            fitness: 0.0,
            chromosome,
        }
    }

    fn chromosome(&self) -> &ga::Chromosome {
        &self.chromosome
    }

    fn fitness(&self) -> f32 {
        self.fitness
    }
}

Вернемся к fn evolve():

// libs/simulation/src/lib.rs
/* ... */

fn evolve(&mut self, rng: &mut dyn RngCore) {
    self.age = 0;

    // Преобразуем `Vec<Animal>` в `Vec<AnimalIndividual>`
    let current_population: Vec<_> = self
        .world
        .animals
        .iter()
        .map(|animal| преобразуем Animal в AnimalIndividual)
        .collect();

    // Эволюционируем этот `Vec<AnimalIndividual>`
    let evolved_population = self.ga.evolve(
        rng,
        &current_population,
    );

    // Преобразуем `Vec<AnimalIndividual>` обратно в `Vec<Animal>`
    self.world.animals = evolved_population
        .into_iter()
        .map(|individual| преобразуем AnimalIndividual в Animal)
        .collect();

    for food in &mut self.world.foods {
        food.position = rng.gen();
    }
}

/* ... */

Кажется, это может сработать!

Для реализации этих map() нам потребуется два метода преобразования:

// libs/simulation/src/animal_individual.rs
/* ... */

impl AnimalIndividual {
    pub fn from_animal(animal: &Animal) -> Self {
        todo!()
    }

    pub fn into_animal(self, rng: &mut dyn RngCore) -> Animal {
        todo!()
    }
}

/* ... */

...что позволяет нам сделать следующее:

/* ... */

fn evolve(&mut self, rng: &mut dyn RngCore) {
    /* ... */

    let current_population: Vec<_> = self
        .world
        .animals
        .iter()
        .map(AnimalIndividual::from_animal)
        .collect();

    /* ... */

    self.world.animals = evolved_population
        .into_iter()
        .map(|individual| individual.into_animal(rng))
        .collect();

    /* ... */
}

/* ... */

Как нам реализовать эти методы?

from_animal

Внесем важные изменения:

// libs/simulation/src/animal_individual.rs
/* ... */

pub struct AnimalIndividual {
    fitness: f32,
    chromosome: ga::Chromosome,
}

impl AnimalIndividual {
    pub fn from_animal(animal: &Animal) -> Self {
        Self {
            fitness: todo!(),
            chromosome: todo!(),
        }
    }

    /* ... */
}

/* ... */

Что нам следует делать внутри ::from_animal()? Две вещи:

1. Определить функцию приспособленности птицы.
2. Определить хромосому (генотип) птицы.

Вычислить показатель приспособленности довольно просто: мы уже обрабатываем столкновения, поэтому нам всего лишь нужно их посчитать:

// libs/simulation/src/animal.rs
/* ... */

#[derive(Debug)]
pub struct Animal {
    /* ... */

    /// Количество еды, съеденной этой птицей
    pub(crate) satiation: usize,
}

impl Animal {
    pub fn random(rng: &mut dyn RngCore) -> Self {
        /* ... */

        Self {
            /* ... */
            satiation: 0,
        }
    }

    /* ... */
}

/* ... */

// libs/simulation/src/lib.rs
/* ... */

impl Simulation {
    /* ... */

    fn process_collisions(&mut self, rng: &mut dyn RngCore) {
        for animal in &mut self.world.animals {
            for food in &mut self.world.foods {
                /* ... */

                if distance <= 0.01 {
                    animal.satiation += 1;
                    food.position = rng.gen();
                }
            }
        }
    }

    /* ... */
}

/* ... */

// libs/simulation/src/animal_individual.rs
/* ... */

impl AnimalIndividual {
    pub fn from_animal(animal: &Animal) -> Self {
        Self {
            fitness: animal.satiation as f32,
            chromosome: todo!(),
        }
    }

    /* ... */
}

/* ... */

Обожаю, когда все детали просто складываются вместе.

Что касается второго поля, chromosome, то здесь работы будет немного больше. Напомним, что под хромосомой здесь мы подразумеваем веса нейронной сети, поэтому в идеале мы должны написать:

// libs/simulation/src/animal_individual.rs
/* ... */

impl AnimalIndividual {
    pub fn from_animal(animal: &Animal) -> Self {
        Self {
            /* ... */
            chromosome: animal.brain.weights(),
        }
    }

    /* ... */
}

/* ... */

...но Network из lib-neural-network не имеет такого метода... пока!

Для реализации weights(), вернемся к lib-neural-network - мы ищем следующее:

// libs/neural-network/src/lib.rs
/* ... */

impl Network {
    /* ... */

    pub fn weights(&self) -> Vec<f32> {
        todo!()
    }
}

/* ... */

Ради интереса начнем с теста:

// libs/neural-network/src/lib.rs
/* ... */

#[cfg(test)]
mod tests {
    /* ... */

   #[test]
   fn weights() {
       let network = Network {
           layers: vec![
               Layer {
                   neurons: vec![Neuron {
                       bias: 0.1,
                       weights: vec![0.2, 0.3, 0.4],
                   }],
               },
               Layer {
                   neurons: vec![Neuron {
                       bias: 0.5,
                       weights: vec![0.6, 0.7, 0.8],
                   }],
               },
           ],
       };

       let actual = network.weights();
       let expected = vec![0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8];

       assert_relative_eq!(actual.as_slice(), expected.as_slice());
   }
}

Что касается реализации, я покажу вам три - одна использует циклы for, а две другие - комбинаторы:

1. Циклы:

// libs/neural-network/src/lib.rs
impl Network {
    /* ... */

    pub fn weights(&self) -> Vec<f32> {
        let mut weights = Vec::new();

        for layer in &self.layers {
            for neuron in &layer.neurons {
                weights.push(neuron.bias);

                for weight in &neuron.weights {
                    weights.push(*weight);
                }
            }
        }

        weights
    }
}

2. Комбинаторы:

use std::iter::once;

/* ... */

impl Network {
    /* ... */

    pub fn weights(&self) -> Vec<f32> {
        self.layers
            .iter()
            .flat_map(|layer| layer.neurons.iter())
            .flat_map(|neuron| once(&neuron.bias).chain(&neuron.weights))
            .copied()
            .collect()
    }
}

3. Комбинаторы + итератор:

use std::iter::once;

/* ... */

impl Network {
    /* ... */

    pub fn weights(&self) -> impl Iterator<Item = f32> + '_ {
        self.layers
            .iter()
            .flat_map(|layer| layer.neurons.iter())
            .flat_map(|neuron| once(&neuron.bias).chain(&neuron.weights))
            .copied()
    }
}

/* ... */

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn weights() {
        /* ... */

        let actual: Vec<_> = network.weights().collect();

        /* ... */
    }
}

Я считаю, что последний подход лучше, потому что он позволяет избежать выделения памяти для вектора, но когда дело доходит до продашкна, поддерживаемость обычно важнее производительности, поэтому последнее слово за вами.

Кроме того, пока мы здесь, реализуем обратную операцию - ::from_weights():

/* ... */

impl Network {
    /* ... */

    pub fn from_weights(
        layers: &[LayerTopology],
        weights: impl IntoIterator<Item = f32>,
    ) -> Self {
        todo!()
    }

    /* ... */
}

/* ... */

В идеале мы хотели бы, чтобы выполнялось следующее условие:

network == Network::from_weights(network.weights())

...напишем тесты, исходя из этого:

/* ... */

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn from_weights() {
        let layers = &[
            LayerTopology { neurons: 3 },
            LayerTopology { neurons: 2 },
        ];

        let weights = vec![0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8];
        let network = Network::from_weights(layers, weights.clone());
        let actual: Vec<_> = network.weights().collect();

        assert_relative_eq!(actual.as_slice(), weights.as_slice());
    }

    /* ... */
}

...тогда реализация может выглядеть так:

// libs/neural-network/src/lib.rs
/* ... */

impl Network {
    /* ... */

    pub fn from_weights(
        layers: &[LayerTopology],
        weights: impl IntoIterator<Item = f32>,
    ) -> Self {
        assert!(layers.len() > 1);

        let mut weights = weights.into_iter();

        let layers = layers
            .windows(2)
            .map(|layers| {
                Layer::from_weights(
                    layers[0].neurons,
                    layers[1].neurons,
                    &mut weights,
                )
            })
            .collect();

        if weights.next().is_some() {
            panic!("получено слишком много весов");
        }

        Self { layers }
    }

    /* ... */
}

impl Layer {
    /* ... */

    fn from_weights(
        input_size: usize,
        output_size: usize,
        weights: &mut dyn Iterator<Item = f32>,
    ) -> Self {
        let neurons = (0..output_size)
            .map(|_| Neuron::from_weights(input_size, weights))
            .collect();

        Self { neurons }
    }

    /* ... */
}

impl Neuron {
    /* ... */

    fn from_weights(
        input_size: usize,
        weights: &mut dyn Iterator<Item = f32>,
    ) -> Self {
        let bias = weights.next().expect("получено недостаточно весов");

        let weights = (0..input_size)
            .map(|_| weights.next().expect("получено недостаточно весов"))
            .collect();

        Self { bias, weights }
    }

    /* ... */
}

Воссоздать сеть на основе весов довольно сложно, поэтому не волнуйтесь, если понимание этого код займет некоторое время - на его написание тоже ушло некоторое время!

Рефакторинг

В Network теперь есть все необходимое, чтобы сделать ее совместимой с генетическим алгоритмом, но сначала немного отрефакторим одну вещь.

Внутри Animal мы имеем следующее:

// libs/simulation/src/animal.rs
/* ... */

#[derive(Debug)]
pub struct Animal {
    /* ... */
    pub(crate) brain: nn::Network,
    /* ... */
}

/* ... */

...и я хочу вынести brain: nn::Network в отдельную, эм, часть тела:

// libs/simulation/src/lib.rs
/* ... */

pub use self::{animal::*, brain::*, eye::*, food::*, world::*};

mod animal;
mod animal_individual;
mod brain;
/* ... */

// libs/simulation/src/brain.rs
use crate::*;

#[derive(Debug)]
pub struct Brain {
    pub(crate) nn: nn::Network,
}

impl Brain {
    pub fn random(rng: &mut dyn RngCore, eye: &Eye) -> Self {
        Self {
            nn: nn::Network::random(rng, &Self::topology(eye)),
        }
    }

    pub(crate) fn as_chromosome(&self) -> ga::Chromosome {
        self.nn.weights().collect()
    }

    fn topology(eye: &Eye) -> [nn::LayerTopology; 3] {
        [
            nn::LayerTopology {
                neurons: eye.cells(),
            },
            nn::LayerTopology {
                neurons: 2 * eye.cells(),
            },
            nn::LayerTopology { neurons: 2 },
        ]
    }
}

// libs/simulation/src/animal.rs
/* ... */

#[derive(Debug)]
pub struct Animal {
    /* ... */
    pub(crate) brain: Brain,
    /* ... */
}

impl Animal {
    pub fn random(rng: &mut dyn RngCore) -> Self {
        let eye = Eye::default();
        let brain = Brain::random(rng, &eye);

        Self::new(eye, brain, rng)
    }

    pub(crate) fn as_chromosome(&self) -> ga::Chromosome {
        // Мы эволюционируем только мозг птиц, но технически можно
        // симулировать, например, их физические свойства, такие как размер.
        //
        // Эта функция может быть настроена для возврата более длинной хромосомы,
        // кодирующей не только мозг, но и, скажем, цвет птички.

        self.brain.as_chromosome()
    }

    /* ... */

    fn new(eye: Eye, brain: Brain, rng: &mut dyn RngCore) -> Self {
        Self {
            position: rng.gen(),
            rotation: rng.gen(),
            speed: 0.002,
            eye,
            brain,
            satiation: 0,
        }
    }
}

// libs/simulation/src/lib.rs
fn process_brains(&mut self) {
    for animal in &mut self.world.animals {
        /* ... */

        let response = animal.brain.nn.propagate(vision);

        /* ... */
    }
}

Все это позволяет нам завершить AnimalIndividual::from_animal():

// libs/simulation/src/animal_individual.rs
/* ... */

impl AnimalIndividual {
    pub fn from_animal(animal: &Animal) -> Self {
        Self {
            fitness: animal.satiation as f32,
            chromosome: animal.as_chromosome(),
        }
    }

    /* ... */
}

/* ... */

Снова все части идеально сочетаются вместе 🥳

into_animal

Теперь мы можем преобразовать Animal в AnimalIndividual и отправить его в генетический алгоритм. Пришло время реализовать обратную операцию - преобразование нового AnimalIndividual, полученного из генетического алгоритма, в Animal:

// libs/simulation/src/animal_individual.rs
/* ... */

impl AnimalIndividual {
    /* ... */

    pub fn into_animal(self, rng: &mut dyn RngCore) -> Animal {
        Animal::from_chromosome(self.chromosome, rng)
    }
}

/* ... */

// libs/simulation/src/animal.rs
/* ... */

impl Animal {
    /* ... */

    /// "Восстанавливает" птицу из хромосомы.
    ///
    /// Мы должны иметь доступ к ГПСЧ здесь, поскольку наши
    /// хромосомы кодируют только мозг - в процессе восстановления птицы
    /// мы должны рандомизировать ее позицию, направление и др.
    pub(crate) fn from_chromosome(
        chromosome: ga::Chromosome,
        rng: &mut dyn RngCore,
    ) -> Self {
        let eye = Eye::default();
        let brain = Brain::from_chromosome(chromosome, &eye);

        Self::new(eye, brain, rng)
    }

    pub(crate) fn as_chromosome(&self) -> ga::Chromosome {
        self.brain.as_chromosome()
    }

    /* ... */
}

/* ... */

// libs/simulation/src/brain.rs
/* ... */

impl Brain {
    /* ... */

    pub(crate) fn from_chromosome(
        chromosome: ga::Chromosome,
        eye: &Eye,
    ) -> Self {
        Self {
            nn: nn::Network::from_weights(
                &Self::topology(eye),
                chromosome,
            ),
        }
    }

    pub(crate) fn as_chromosome(&self) -> ga::Chromosome {
        self.nn.weights().collect()
    }

    /* ... */
}

Смотрите-ка... мы закончили! Мы закончили?

На старт, внимание...

Мы вроде как закончили. Хотя мы можем просто запустить wasm-pack build, взять бинокль и наблюдать за птицами, можно сделать две вещи, чтобы улучшить опыт наблюдения:

1. Во-первых, поскольку эволюция происходит раз в 2500 шагов, а мы выполняем 60 шагов в секунду (на один кадр приходится один шаг, а браузер старается поддерживать стабильные 60 FPS (frames per second - кадры в секунду) (зависит от дисплея)), то в реальности эволюция происходит один раз примерно в 40 секунд.

Если мы хотим увидеть, как птички становятся все умнее и умнее, нам придется ждать около 10 поколений (говорю по опыту), то есть примерно 6,5 минут. 6,5 минут гипнотизировать экран - какая пустая трата времени!

Вот бы у нас была кнопка "перемотки вперед"...​

2. Во-вторых, даже если эволюция работает (с большим акцентом на "если", потому что мы скептики!), в данный момент мы не можем это проверить.

Действительно ли наши нынешние птицы летают лучше, чем те, что были, скажем, десять минут назад?

К счастью для нас, поскольку мы цифровые, найти доказательства эволюции довольно легко: мы просто улучшим lib-genetic-algorithm так, чтобы он возвращал статистику, например, средний показатель приспособленности, и воспользуемся console.log(), чтобы увидеть, улучшается ли эта статистика.

Наше путешествие подходит к концу - код, который мы напишем через минуту, станет кульминацией проделанной нами тяжелой работы.

Перемотка и статистика

В JS мы вызываем step() только во время redraw() - именно поэтому наша симуляция "застревает" на 60 FPS:

// www/index.js
/* ... */

function redraw() {
    /* ... */

    simulation.step();

    /* ... */
}

/* ... */

Для ускорения симуляции мы можем вызывать step() несколько раз одновременно:

/* ... */

function redraw() {
    /* ... */

    // Выполняем 10 шагов за один кадр, что делает нашу симуляцию в 10 раз быстрее
    // (если ваша машина потянет!)
    for (let i = 0; i < 10; i += 1) {
        simulation.step();
    }

    /* ... */
}

/* ... */

...или, что еще лучше, мы можем предоставить специальный метод, который "перематывает" целое поколение - таким образом, симуляцию можно поддерживать на скорости 1x и привязать "перемотку" к кнопке, чтобы перематывать по требованию:

// libs/simulation/src/lib.rs
/* ... */

impl Simulation {
    /* ... */

    pub fn step(&mut self, rng: &mut dyn RngCore) -> bool {
        /* ... */

        self.age += 1;

        if self.age > GENERATION_LENGTH {
            self.evolve(rng);
            true
        } else {
            false
        }
    }

    /// Перематываем до конца текущего поколения
    pub fn train(&mut self, rng: &mut dyn RngCore) {
        loop {
            if self.step(rng) {
                return;
            }
        }
    }

    /* ... */
}

// libs/simulation-wasm/src/lib.rs
/* ... */

#[wasm_bindgen]
impl Simulation {
    /* ... */

    pub fn train(&mut self) {
        self.sim.train(&mut self.rng);
    }
}

/* ... */

<!-- www/index.html -->
<!-- ... -->
<style>
  /* ... */

  #train {
      position: absolute;
      top: 0;
      margin: 15px;
  }
</style>
<body>
  <canvas id="viewport" width="800" height="800"></canvas>
  <button id="train">Тренировать</button>
  <script src="./bootstrap.js"></script>
</body>
<!-- ... -->

// www/index.js
import * as sim from "lib-simulation-wasm";

let simulation = new sim.Simulation();

document.getElementById('train').addEventListener("click", simulation.train);

const viewport = document.getElementById('viewport');
const viewportScale = window.devicePixelRatio || 1;

/* ... */

Погодите, разве этот код не требует RwLock или Mutex?

Если пользователь нажмет на кнопку "Тренировать" во время работы step(), не приведет ли это к тому, что наш код Rust выполнится два раза, уничтожив Вселенную и все, что мы любим?

Бояться нечего, JS однопоточный - когда браузер выполняет step() (или, скорее, redraw()), он "подвешивает" вкладку.

Немного упрощая, можно сказать, что одновременно выполняется только одна строка кода JS - невозможно выполнить одновременно step() и train() (что также нарушило бы требование &mut self на стороне Rust). Если пользователь нажимает на кнопку "Тренировать" во время работы step(), браузер планирует выполнение этого события в следующем кадре.

Хорошо, теперь, когда мы можем ускорить эволюцию, займемся статистикой - самое простое, что у нас есть под рукой, - это показатели приспособленности, поэтому lib-genetic-algorithm кажется хорошим местом для реализации сбора статистики:

// libs/genetic-algorithm/src/lib.rs
impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(/* ... */) -> (Vec<I>, Statistics)
    where
        I: Individual,
    {
        assert!(!population.is_empty());

        let new_population = (0..population.len())
            .map(|_| {
                /* ... */
            })
            .collect();

        let stats = Statistics::new(population);

        (new_population, stats)
    }
}

/* ... */

#[derive(Clone, Debug)]
pub struct Statistics {
    pub min_fitness: f32,
    pub max_fitness: f32,
    pub avg_fitness: f32,
}

impl Statistics {
    fn new<I>(population: &[I]) -> Self
    where
        I: Individual,
    {
        assert!(!population.is_empty());

        let mut min_fitness = population[0].fitness();
        let mut max_fitness = min_fitness;
        let mut sum_fitness = 0.0;

        for individual in population {
            let fitness = individual.fitness();

            min_fitness = min_fitness.min(fitness);
            max_fitness = max_fitness.max(fitness);
            sum_fitness += fitness;
        }

        Self {
            min_fitness,
            max_fitness,
            avg_fitness: sum_fitness / (population.len() as f32),
        }
    }
}

// libs/simulation/src/lib.rs
/* ... */

impl Simulation {
    /* ... */

    pub fn step(&mut self, rng: &mut dyn RngCore) -> Option<ga::Statistics> {
        /* ... */

        if self.age > GENERATION_LENGTH {
            Some(self.evolve(rng))
        } else {
            None
        }
    }

    pub fn train(&mut self, rng: &mut dyn RngCore) -> ga::Statistics {
        loop {
            if let Some(summary) = self.step(rng) {
                return summary;
            }
        }
    }

    /* ... */

    fn evolve(&mut self, rng: &mut dyn RngCore) -> ga::Statistics {
        /* ... */

        let (evolved_population, stats) = self.ga.evolve(rng, &current_population);

        /* ... */

        stats
    }
}

// libs/simulation-wasm/src/lib.rs
/* ... */

#[wasm_bindgen]
impl Simulation {
    /* ... */

    /// min = минимальное количество еды, съеденное любой птицей
    ///
    /// max = максимальное количество еды, съеденное любой птицей
    ///
    /// avg = количество еды, съеденной всеми птицами,
    ///       деленная на количество птиц
    ///
    /// Медиана также может быть полезной!
    pub fn train(&mut self) -> String {
        let stats = self.sim.train(&mut self.rng);

        format!(
            "min={:.2}, max={:.2}, avg={:.2}",
            stats.min_fitness,
            stats.max_fitness,
            stats.avg_fitness,
        )
    }
}

// www/index.js
/* ... */

document.getElementById('train').addEventListener("click", () => {
    console.log(simulation.train());
});

/* ... */

На этот раз при сборке не забудьте о флаге --release для оптимизации работы train():

wasm-pack build --release

...
[INFO]: :-) Done in 40.00s
[INFO]: :-) Your wasm pkg is ready to publish at /home/pwy/Projects/...

На старт, внимание, марш!

Вы готовы?

Хорошо?

• Птички милые? ✅
• Птички едят еду? ✅
• Птички ловят еду лучше и лучше (учатся)? ✅

Хорошо!

Конкретные статистические данные, которые вы получите, скорее всего, будут отличаться от моих, но общая тенденция - повышение минимального, максимального и среднего значения - должна быть видна в большинстве симуляций.

Результаты не будут расти до бесконечности - судя по тому, что я видел, в большинстве случаев вы будете получать лучшие значения до 40–50 поколения.

Также помните, что мы сильно полагаемся на произвольные числа! Если вам кажется, что птицы слишком рано застревают в локальном оптимуме, попробуйте перезапустить симуляцию.

Заключительные мысли

Мы начали с самых основ, не так ли?

На основе грубых набросков и нашей первой struct Network мы разработали генетический алгоритм, реализовали тесты для зрения (как здорово!) и в итоге получили кучу самоуправляющихся птичек, которые не так уж плохи, учитывая количество кода!

Я надеюсь, что эта серия помогла вам понять изрядную долю идиом Rust, методов тестирования, а также, что я выполнил свое обещание использовать WA интересным способом.

Это вам:

Что дальше?

Если вы хотите немного поработать самостоятельно, осталось несколько интересных задач!

Помните все эти константы, такие как FOV_RANGE?

Если вместо жесткого кодирования, сделать эти константы настраиваемыми с помощью некоторой struct Config, можно создать приложение, проверяющее разные комбинации этих параметров с целью определения наиболее оптимальных:

let mut stats = Vec::new();

for fov_range in vec![0.1, 0.2, 0.3, 0.4, ..., PI] {
    for fov_distance in vec![0.1, 0.2, 0.3, 0.4, ..., 1.0] {
        let current_stats = run_simulation(
            fov_range,
            fov_distance,
            /* ... */,
        );

        stats.push((fov_range, fov_distance, current_stats));
    }
}

// TODO используя `stats`, выяснить комбинации, приводящие к лучшим результатам

Бонусные баллы за использование rayon!

Исходный код проекта, немного отрефакторенный, можно найти здесь.