Структуры данных, реализованные на JavaScript
Связный список
Описание
Свя�зный (или связанный, или односвязный, или однонаправленный) список (linked list) - это динамическая структура данных, представляющая собой упорядоченную коллекцию узлов (nodes). Каждый узел содержит значение и ссылку (указатель) на следующий узел.

Преимущество связного списка перед массивом заключается в его структурной гибкости: порядок элементов связного списка может не совпадать с порядком их расположения в памяти. Порядок обхода (traverse) списка задается его внутренними связями. Суть преимущества состоит в том, что во многих языках программирования создание массива требует указания его размера (для выделения необходимой памяти), а связный список позволяет обойти это ограничение.
Недостатком связного списка является то, что время доступа к его элементам линейно (соответствует количеству элементов). Быстрый (произвольный) доступ к элементу невозможен.
Сложность
Временная
| Чтение | Поиск | Вставка | Удаление |
|---|---|---|---|
| O(n) | O(n) | O(1) | O(n) |
Пространственная
O(n)
Реализация
Начнем с реализации вспомогательной функции сравнения узлов:
// utils/comparator.js
export default class Comparator {
constructor(fn) {
this.compare = fn || Comparator.defaultCompare
}
// Дефолтная функция сравнения узлов
static defaultCompare(a, b) {
if (a === b) {
return 0
}
return a < b ? -1 : 1
}
// Проверка на равенство
equal(a, b) {
return this.compare(a, b) === 0
}
// Меньше чем
lessThan(a, b) {
return this.compare(a, b) < 0
}
// Больше чем
greaterThan(a, b) {
return this.compare(a, b) > 0
}
// Меньше или равно
lessThanOrEqual(a, b) {
return this.lessThan(a, b) || this.equal(a, b)
}
// Больше или равно
greaterThanOrEqual(a, b) {
return this.greaterThan(a, b) || this.equal(a, b)
}
// Инверсия сравнения
reverse() {
const original = this.compare
this.compare = (a, b) => original(b, a)
}
}
Эта функция позволяет создавать списки с узлами, значения которых являются не только примитивами, но и объектами.
Реализуем узел списка:
// data-structures/linked-list.js
// Узел
class Node {
constructor(value, next = null) {
// Значение
this.value = value
// Ссылка на следующий узел
this.next = next
}
// Возвращает строковое представление узла.
// Принимает кастомную функцию стрингификации
toString(cb) {
return cb ? cb(this.value) : `${this.value}`
}
}
Приступаем к реализации связного списка:
import Comparator from '../utils/comparator'
export default class LinkedList {
constructor(fn) {
// Головной (первый) узел
this.head = null
// Хвостовой (последний) узел
this.tail = null
// Функция сравнения узлов
this.compare = new Comparator(fn)
}
}
Начнем с методов добавления узла в начало и конец списка:
// Добавляет значение в начало списка
prepend(value) {
// Создаем новый головной узел со ссылкой на предыдущий головной узел
// (новый узел становится головным (первым))
this.head = new Node(value, this.head)
// Если хвостовой узел отсутствует, значит,
if (!this.tail) {
// головной узел также является хвостовым
this.tail = this.head
}
// Это обеспечивает возможность вызова методов по цепочке
return this
}
// Добавляет значение в конец списка
append(value) {
// Создаем новый узел
const node = new Node(value)
// Если головной узел отсутствует, то
if (!this.head) {
// добавляем значение в начало списка
return this.prepend(value)
}
// Добавляем ссылку на новый узел в хвостовой
this.tail.next = node
// Обновляем хвостовой узел
// (новый узел становится хвостовым (последним))
this.tail = node
return this
}
Метод добавления узла в указанную позицию (по индексу):
// Добавляет значение в список по указанному индексу
insert(value, index) {
// Если индекс равен 0, то
if (index === 0) {
// Добавляем значение в начало списка
return this.prepend(value)
}
// Создаем новый узел
const node = new Node(value)
// Текущий узел (начинаем с головного)
let current = this.head
// Счетчик
let i = 1
// Пока есть текущий узел
while (current) {
// Прерываем цикл при совпадении счетчика с индексом -
// это означает, что мы нашли нужный узел
if (i === index) {
break
}
// Переходим к следующему узлу
current = current.next
// Увеличиваем значение счетчика
i += 1
}
// Если узел найден
if (current) {
// Добавляем ссылку на следующий узел в новый
node.next = current.next
// Обновляем ссылку текущего узла на следующий
// (новый узел помещается между текущим и следующим: current и current.next)
current.next = node
} else {
// Если узел не найден,
// добавляем значение в конец списка
return this.append(value)
}
return this
}
Методы удаления головного (первого) и хвостового (последнего) узлов:
// Удаляет головной узел
removeHead() {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - удалять нечего
return null
}
// Удаляемый узел - головной
const removed = this.head
// Если головной узел содержит ссылку на следующий
if (this.head.next) {
// Обновляем головной узел (заменяем на следующий)
this.head = this.head.next
} else {
// Иначе, обнуляем головной и хвостовой узлы,
// (делаем список пустым, поскольку он содержал только один узел)
this.head = null
this.tail = null
}
// Возвращаем удаленный узел
return removed
}
// Удаляет хвостовой узел
removeTail() {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - удалять нечего
return null
}
// Удаляемый узел - хвостовой
let removed = this.tail
// Крайний случай: если список состоит из одного узла,
if (this.head === this.tail) {
// обнуляем головной и хвостовой узлы
// (делаем список пустым)
this.head = null
this.tail = null
// Возвращаем удаленный узел
return removed
}
// Текущий узел (начинаем с головного)
let current = this.head
// Обнуляем ссылку на следующий узел.
// Пока есть следующий узел
while (current.next) {
// Если следующий узел является последним
// (не содержит ссылки на следующий),
if (!current.next.next) {
// обнуляем ссылку текущего узла на следующий
current.next = null
} else {
// Иначе, переходим к следующему узлу
current = current.next
}
}
// Обновляем хвостовой узел (заменяем на текущий)
this.tail = current
// Возвращаем удаленный узел
return removed
}
Метод удаления узла по значению:
// Удаляет узел по значению
remove(value) {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - удалять нечего
return null
}
// Последний удаленный узел
let removed = null
// Пока есть и удаляется головной узел
while (this.head && this.compare.equal(this.head.value, value)) {
// Обновляем удаляемый узел
removed = this.head
// Обновляем головной узел (заменяем на следующий)
this.head = this.head.next
}
// Текущий узел (начинаем с головного)
let current = this.head
// Если узел имеется
if (current) {
// Пока есть следующий узел
while (current.next) {
// Если значения совпадают
if (this.compare.equal(current.next.value, value)) {
// Обновляем удаляемый узел
removed = current.next
// Обновляем ссылку текущего узла (заменяем на следующий,
// чтобы закрыть образовавшуюся брешь)
current.next = current.next.next
} else {
// Иначе, переходим к следующему узлу
current = current.next
}
}
}
// Крайний случай: если удаляется хвостовой узел,
if (this.compare.equal(this.tail.value, value)) {
// обновляем его (заменяем на текущий)
this.tail = current
}
// Возвращаем удаленный узел
return removed
}
Метод поиска узла по значению:
// Ищет узел по значению.
// Принимает искомое значение и функцию поиска
// в ви�де объекта
find({ value, cb }) {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - искать нечего
return null
}
// Текущий узел (начинаем с головного)
let current = this.head
// Пока есть текущий узел
while (current) {
// Если передана функция, и она удовлетворяется,
if (cb && cb(current.value)) {
// возвращаем текущий узел
return current
}
// Если передано значение, и значения совпадают,
if (value && this.compare.equal(current.value, value)) {
// возвращаем текущий узел
return current
}
// Переходим к следующему узлу
current = current.next
}
// Ничего не найдено
return null
}
Метод инвертирования списка:
// Инвертирует список
reverse() {
// Текущий узел (начинаем с головного)
let current = this.head
// Предыдущий узел
let prev = null
// Следующий узел
let next = null
// Пока есть текущий узел
while (current) {
// Обновляем переменную для следующего узла
next = current.next
// Обновляем ссы�лку текущего узла на предыдущий
current.next = prev
// Обновляем переменную для предыдущего узла
prev = current
// Переходим к следующему узлу
current = next
}
// Меняем местами головной и хвостовой узлы
this.tail = this.head
// Обновляем головной узел
// (заменяем последним предыдущим - хвостовым)
this.head = prev
return this
}
Напоследок реализуем несколько вспомогательных методов:
// Создает список из массива
fromArray(arr) {
// Перебираем элементы массива и добавляем каждый в конец списка
arr.forEach((value) => this.append(value))
return this
}
// Преобразует список в массив
toArray() {
// Массив узлов
const arr = []
// Текущий узел (начинаем с головного)
let current = this.head
// Пока есть текущий узел
while (current) {
// Добавляем узел в массив
arr.push(current)
// Переходим к следующему узлу
current = current.next
}
// Возвращаем массив
return arr
}
// Возвращает строковое представление списка.
// Принимает кастомную функцию стрингификации
toString(cb) {
// Преобразуем список в массив
return (
this.toArray()
// Перебираем узлы списка и преобразуем каждый в строку
.map((node) => node.toString(cb))
// Преобразуем массив в строку
.toString()
)
}
Полный код связного списка
import Comparator from '../utils/comparator'
// Узел
export class Node {
constructor(value, next = null) {
// Значение
this.value = value
// Ссылка на следующий узел
this.next = next
}
// Возвращает строковое представление узла.
// Принимает кастомную функцию стрингификации
toString(cb) {
return cb ? cb(this.value) : `${this.value}`
}
}
// Связный список
export default class LinkedList {
constructor(fn) {
// Головной (первый) узел
this.head = null
// Хвостовой (последний) узел
this.tail = null
// Функция сравнения узлов
this.compare = new Comparator(fn)
}
// Добавляет значения в начало списка
prepend(value) {
// Создаем новый головной узел со ссылкой на предыдущий головной узел
// (новый узел становится головным (первым))
this.head = new Node(value, this.head)
// Если хвостовой узел отсутствует, значит,
if (!this.tail) {
// головной узел также является хвостовым
this.tail = this.head
}
// Это обеспечивает возможность вызова методов по цепочке
return this
}
// Добавляет значение в конец списка
append(value) {
// Создаем новый узел
const node = new Node(value)
// Если головной узел отсутствует, то
if (!this.head) {
// добавляем значение в начало списка
return this.prepend(value)
}
// Добавляем ссылку на новый узел в хвостовой узел
this.tail.next = node
// Обновляем хвостовой узел
// (новый узел становится хвостовым (последним))
this.tail = node
return this
}
// Добавляет значение в список по указанному индексу
insert(value, rawIndex) {
// Нормализуем индекс
const index = rawIndex < 0 ? 0 : rawIndex
// Если индекс равен 0, то
if (index === 0) {
// Добавляем значение в начало списка
return this.prepend(value)
}
// Создаем новый узел
const node = new Node(value)
// Текущий узел (начинаем с головного)
let current = this.head
// Счетчик
let i = 1
// Пока есть текущий узел
while (current) {
// Прерываем цикл при совпадении счетчика с индексом -
// это означает, что мы нашли нужный узел
if (i === index) {
break
}
// Переходим к следующему узлу
current = current.next
// Увеличиваем значение счетчика
i += 1
}
// Если узел найден
if (current) {
// Добавляем ссылку на следующий узел в новый
node.next = current.next
// Обновляем ссылку текущего узла на следующий
// (новый узел помещается между текущий и следующим: current и current.next)
current.next = node
} else {
// Если узел не найден,
// добавляем значение в конец списка
return this.append(value)
}
return this
}
// Удаляет головной узел
removeHead() {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - удалять нечего
return null
}
// Удаляемый узел - головной
const removed = this.head
// Если головной узел содержит ссылку на следующий
if (this.head.next) {
// Обновляем головной узел (заменяем на следующий)
this.head = this.head.next
} else {
// Иначе, обнуляем головной и хвостовой узлы,
// (делаем список пустым, поскольку он содержал только один узел)
this.head = null
this.tail = null
}
// Возвращаем удаленный узел
return removed
}
// Удаляет хвостовой узел
removeTail() {
// Если головной узел отсутствует, значит,
if (!this.head) {
// спис�ок пуст - удалять нечего
return null
}
// Удаляемый узел - хвостовой
let removed = this.tail
// Крайний случай: если список состоит из одного узла,
if (this.head === this.tail) {
// обнуляем головной и хвостовой узлы
// (делаем список пустым)
this.head = null
this.tail = null
// Возвращаем удаленный узел
return removed
}
// Текущий узел (начинаем с головного)
let current = this.head
// Обнуляем ссылку на следующий узел.
// Пока есть следующий узел
while (current.next) {
// Если следующий узел является последним
// (не содержит ссылки на следующий),
if (!current.next.next) {
// обнуляем ссылку текущего узла на следующий
current.next = null
} else {
// Иначе, переходим к следующему узлу
current = current.next
}
}
// Обновляем хвостовой узел (заменяем на текущий)
this.tail = current
// Возвращаем удаленный узел
return removed
}
// Удаляет узел по значению
remove(value) {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - удалять нечего
return null
}
// Последний удаленный узел
let removed = null
// Пока есть и удаляется головной узел
while (this.head && this.compare.equal(this.head.value, value)) {
// Обновляем удаляемый узел
removed = this.head
// Обновляем головной узел (заменяем на следующий)
this.head = this.head.next
}
// Текущий узел (начинаем с головного)
let current = this.head
// Если узел имеется
if (current) {
// Пока есть следующий узел
while (current.next) {
// Если значения совпадают
if (this.compare.equal(current.next.value, value)) {
// Обновляем удаляемый узел
removed = current.next
// Обновляем ссылку текущего узла (заменяем на следующий,
// чтобы закрыть образовавшуюся брешь)
current.next = current.next.next
} else {
// Иначе, переходим к следующему узлу
current = current.next
}
}
}
// Крайний случай: если удаляется хвостовой узел,
if (this.compare.equal(this.tail.value, value)) {
// обновляем его (заменяем на текущий)
this.tail = current
}
// Возвращаем удаленный узел
return removed
}
// Ищет узел по значению.
// Принимает искомое значение и функцию поиска
// в виде объекта
find({ value, cb }) {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - искать нечего
return null
}
// Текущий узел (начинаем с головного)
let current = this.head
// Пока есть текущий узел
while (current) {
// Если передана функция, и она удовлетворяется,
if (cb && cb(current.value)) {
// возвращаем текущий узел
return current
}
// Если передано значение, и значения совпадают,
if (value && this.compare.equal(current.value, value)) {
// возвращаем текущий узел
return current
}
// Переходим к следующему узлу
current = current.next
}
// Ничего не найдено
return null
}
// Инвертирует список
reverse() {
// Текущий узел (начинаем с головного)
let current = this.head
// Предыдущий узел
let prev = null
// Следующий узел
let next = null
// Пока есть текущий узел
while (current) {
// Обновляем переменную для следующего узла
next = current.next
// Обновляем ссылку текущего узла на предыдущий
current.next = prev
// Обновляем переменную для предыдущего узла
prev = current
// Переходим к следующему узлу
current = next
}
// Меняем местами головной и хвостовой узлы
this.tail = this.head
// Обновляем головной узел
// (заменяем последним предыдущим - хвостовым)
this.head = prev
return this
}
// Создает список из массива
fromArray(arr) {
// Перебираем элементы массива и добавляем каждый в конец списка
arr.forEach((value) => this.append(value))
return this
}
// Преобразует список в массив
toArray() {
// Массив узлов
const arr = []
// Текущий узел (начинаем с головного)
let current = this.head
// Пока есть текущий узел
while (current) {
// Добавляем узел в массив
arr.push(current)
// Переходим к следующему узлу
current = current.next
}
// Возвращаем массив
return arr
}
// Возвращает строковое представление списка.
// Принимает кастомную функцию стрингификации
toString(cb) {
// Преобразуем список в массив
return (
this.toArray()
// Перебираем узлы и преобразуем каждый в строку
.map((node) => node.toString(cb))
// Преобразуем массив в строку
.toString()
)
}
}
Тестирование
Проверим, что наш связный список работает, как ожидается.
Начнем с узла:
// data-structures/__tests__/linked-list.test.js
import LinkedList, { Node } from '../linked-list'
describe('LinkedListNode', () => {
it('должен создать узел с указанным значением', () => {
const node = new Node(1)
expect(node.value).toBe(1)
expect(node.next).toBeNull()
})
it('должен создать узел с объектом в качестве значения', () => {
const nodeValue = { value: 1, key: 'test' }
const node = new Node(nodeValue)
expect(node.value.value).toBe(1)
expect(node.value.key).toBe('test')
expect(node.next).toBeNull()
})
it('должен соединить узлы вместе', () => {
const node2 = new Node(2)
const node1 = new Node(1, node2)
expect(node1.next).toBeDefined()
expect(node2.next).toBeNull()
expect(node1.value).toBe(1)
expect(node1.next.value).toBe(2)
})
it('должен преобразовать узел в строку', () => {
const node = new Node(1)
expect(node.toString()).toBe('1')
node.value = 'string value'
expect(node.toString()).toBe('string value')
})
it('должен преобразовать узел в строку с помощью кастомной функции', () => {
const nodeValue = { value: 1, key: 'test' }
const node = new Node(nodeValue)
const toStringCallback = (value) =>
`value: ${value.value}, key: ${value.key}`
expect(node.toString(toStringCallback)).toBe('value: 1, key: test')
})
})
Теперь сам список
describe('LinkedList', () => {
it('должен создать пустой связный список', () => {
const linkedList = new LinkedList()
expect(linkedList.toString()).toBe('')
})
it('должен добавить узлы в конец списка', () => {
const linkedList = new LinkedList()
expect(linkedList.head).toBeNull()
expect(linkedList.tail).toBeNull()
linkedList.append(1)
linkedList.append(2)
expect(linkedList.toString()).toBe('1,2')
expect(linkedList.tail.next).toBeNull()
})
it('должен добавить узлы в начало списка', () => {
const linkedList = new LinkedList()
linkedList.prepend(2)
expect(linkedList.head.toString()).toBe('2')
expect(linkedList.tail.toString()).toBe('2')
linkedList.append(1)
linkedList.prepend(3)
expect(linkedList.toString()).toBe('3,2,1')
})
it('должен добавить узлы по указанным индексам', () => {
const linkedList = new LinkedList()
linkedList.insert(4, 3)
expect(linkedList.head.toString()).toBe('4')
expect(linkedList.tail.toString()).toBe('4')
linkedList.insert(3, 2)
linkedList.insert(2, 1)
linkedList.insert(1, -7)
linkedList.insert(10, 9)
expect(linkedList.toString()).toBe('1,4,2,3,10')
})
it('должен удалить узлы по значениям', () => {
const linkedList = new LinkedList()
expect(linkedList.remove(5)).toBeNull()
linkedList.append(1)
linkedList.append(1)
linkedList.append(2)
linkedList.append(3)
linkedList.append(3)
linkedList.append(3)
linkedList.append(4)
linkedList.append(5)
expect(linkedList.head.toString()).toBe('1')
expect(linkedList.tail.toString()).toBe('5')
const removedNode = linkedList.remove(3)
expect(removedNode.value).toBe(3)
expect(linkedList.toString()).toBe('1,1,2,4,5')
linkedList.remove(3)
expect(linkedList.toString()).toBe('1,1,2,4,5')
linkedList.remove(1)
expect(linkedList.toString()).toBe('2,4,5')
expect(linkedList.head.toString()).toBe('2')
expect(linkedList.tail.toString()).toBe('5')
linkedList.remove(5)
expect(linkedList.toString()).toBe('2,4')
expect(linkedList.head.toString()).toBe('2')
expect(linkedList.tail.toString()).toBe('4')
linkedList.remove(4)
expect(linkedList.toString()).toBe('2')
expect(linkedList.head.toString()).toBe('2')
expect(linkedList.tail.toString()).toBe('2')
linkedList.remove(2)
expect(linkedList.toString()).toBe('')
})
it('должен удалить хвостовые узлы', () => {
const linkedList = new LinkedList()
linkedList.append(1)
linkedList.append(2)
linkedList.append(3)
expect(linkedList.head.toString()).toBe('1')
expect(linkedList.tail.toString()).toBe('3')
const removedNode1 = linkedList.removeTail()
expect(removedNode1.value).toBe(3)
expect(linkedList.toString()).toBe('1,2')
expect(linkedList.head.toString()).toBe('1')
expect(linkedList.tail.toString()).toBe('2')
const removedNode2 = linkedList.removeTail()
expect(removedNode2.value).toBe(2)
expect(linkedList.toString()).toBe('1')
expect(linkedList.head.toString()).toBe('1')
expect(linkedList.tail.toString()).toBe('1')
const removedNode3 = linkedList.removeTail()
expect(removedNode3.value).toBe(1)
expect(linkedList.toString()).toBe('')
expect(linkedList.head).toBeNull()
expect(linkedList.tail).toBeNull()
})
it('должен удалить головные узлы', () => {
const linkedList = new LinkedList()
expect(linkedList.removeHead()).toBeNull()
linkedList.append(1)
linkedList.append(2)
expect(linkedList.head.toString()).toBe('1')
expect(linkedList.tail.toString()).toBe('2')
const removedNode1 = linkedList.removeHead()
expect(removedNode1.value).toBe(1)
expect(linkedList.toString()).toBe('2')
expect(linkedList.head.toString()).toBe('2')
expect(linkedList.tail.toString()).toBe('2')
const removedNode2 = linkedList.removeHead()
expect(removedNode2.value).toBe(2)
expect(linkedList.toString()).toBe('')
expect(linkedList.head).toBeNull()
expect(linkedList.tail).toBeNull()
})
it('должен добавить в список значения в виде объектов', () => {
const linkedList = new LinkedList()
const nodeValue1 = { value: 1, key: 'key1' }
const nodeValue2 = { value: 2, key: 'key2' }
linkedList.append(nodeValue1).prepend(nodeValue2)
const nodeStringifier = (value) => `${value.key}:${value.value}`
expect(linkedList.toString(nodeStringifier)).toBe('key2:2,key1:1')
})
it('должен найти узлы по значениям', () => {
const linkedList = new LinkedList()
expect(linkedList.find({ value: 5 })).toBeNull()
linkedList.append(1)
expect(linkedList.find({ value: 1 })).toBeDefined()
linkedList.append(2).append(3)
const node = linkedList.find({ value: 2 })
expect(node.value).toBe(2)
expect(linkedList.find({ value: 5 })).toBeNull()
})
it('должен найти узлы с помощью кастомной функции', () => {
const linkedList = new LinkedList()
linkedList
.append({ value: 1, key: 'test1' })
.append({ value: 2, key: 'test2' })
.append({ value: 3, key: 'test3' })
const node = linkedList.find({ cb: (value) => value.key === 'test2' })
expect(node).toBeDefined()
expect(node.value.value).toBe(2)
expect(node.value.key).toBe('test2')
expect(linkedList.find({ cb: (value) => value.key === 'test5' })).toBeNull()
})
it('должен найти узлы с помощью кастомной функции сравнения', () => {
const comparatorFunction = (a, b) => {
if (a.customValue === b.customValue) {
return 0
}
return a.customValue < b.customValue ? -1 : 1
}
const linkedList = new LinkedList(comparatorFunction)
linkedList
.append({ value: 1, customValue: 'test1' })
.append({ value: 2, customValue: 'test2' })
.append({ value: 3, customValue: 'test3' })
const node = linkedList.find({
value: { value: 2, customValue: 'test2' },
})
expect(node).toBeDefined()
expect(node.value.value).toBe(2)
expect(node.value.customValue).toBe('test2')
expect(
linkedList.find({ value: { value: 2, customValue: 'test5' } }),
).toBeNull()
})
it('должен применять функции для поиска узлов в правильном порядке (сначала применяется функция, переданная в объекте, при вызове метода `find`)', () => {
const greaterThan = (value, compareTo) => (value > compareTo ? 0 : 1)
const linkedList = new LinkedList(greaterThan)
linkedList.fromArray([1, 2, 3, 4, 5])
let node = linkedList.find({ value: 3 })
expect(node.value).toBe(4)
node = linkedList.find({ cb: (value) => value < 3 })
expect(node.value).toBe(1)
})
it('должен создать список из массива', () => {
const linkedList = new LinkedList()
linkedList.fromArray([1, 1, 2, 3, 3, 3, 4, 5])
expect(linkedList.toString()).toBe('1,1,2,3,3,3,4,5')
})
it('должен преобразовать список в массив', () => {
const linkedList = new LinkedList()
linkedList.append(1)
linkedList.append(2)
linkedList.append(3)
expect(linkedList.toArray().join(',')).toBe('1,2,3')
})
it('должен инвертировать список', () => {
const linkedList = new LinkedList()
// Добавляем тестовые значения в список
linkedList.append(1).append(2).append(3)
expect(linkedList.toString()).toBe('1,2,3')
expect(linkedList.head.value).toBe(1)
expect(linkedList.tail.value).toBe(3)
// Инвертируем список
linkedList.reverse()
expect(linkedList.toString()).toBe('3,2,1')
expect(linkedList.head.value).toBe(3)
expect(linkedList.tail.value).toBe(1)
// Инвертируем список обратно в начальное состояние
linkedList.reverse()
expect(linkedList.toString()).toBe('1,2,3')
expect(linkedList.head.value).toBe(1)
expect(linkedList.tail.value).toBe(3)
})
})
Запускаем тесты:
npm run test ./data-structures/__tests__/linked-list
Результат:

Отлично! Двигаемся дальше.
Двусвязный список
Двусвязный (или двунаправленный) список (doubly linked list) похож на односвязный (см. предыдущий раздел), но узлы такого списка, помимо ссылок на следующие узлы, содержат также ссылки на предыдущие узлы, что, собственно, и делает список двусвязным.

Две ссылки позволяют обходить (traverse) список в обоих направлениях. Несмотря на то, что добавление и удаление узлов в двусвязном списке требует изменения бОльшего количества ссылок, сами эти операции проще и потенциально более эффективны (для некорневых узлов), поскольку при обходе списка нам не нужно следить за предыдущим узлом или повторно обходить список в поиске предыдущего узла.
Сложность
Временная
| Чтение | Поиск | Вставка | Удаление |
|---|---|---|---|
| O(n) | O(n) | O(1) | O(n) |
Пространственная
O(n)
Реализация
Начнем с узла:
// data-structures/doubly-linked-list.js
// Узел
export class Node {
constructor(value, next = null, prev = null) {
// Значение
this.value = value
// Ссылка на следующий узел
this.next = next
// Ссылка на предыдущий узел
this.prev = prev
}
// Возвращает строковое представление узла.
// Принимает кастомную функцию стрингификации
toString(cb) {
return cb ? cb(this.value) : `${this.value}`
}
}
Приступаем к реализации двусвязного списка:
// Двусвязный список
export default class DoublyLinkedList {
constructor(fn) {
// Головной (первый) узел
this.head = null
// Хвостовой (последний) узел
this.tail = null
// Функция сравнения узлов
this.compare = new Comparator(fn)
}
}
Начнем с методов добавления узла в начало и конец списка:
// Добавляет значение в начало списка
prepend(value) {
// Создаем новый узел
const node = new Node(value, this.head)
// Если головной узел имеется,
if (this.head) {
// обновляем его ссылку на предыдущий узел
this.head.prev = node
}
// Обновляем головной узел (заменяем на новый)
this.head = node
// Если хвостовой узел отсутствует, значит,
if (!this.tail) {
// головной узел также является хвостовым
// (список был пустым)
this.tail = node
}
// Это обеспечивает возможность вызова методов по цепочке
return this
}
// Добавляет значение в конец списка
append(value) {
// Если головной узел отсутствует,
if (!this.head) {
// добавляем значение в начало списка
return this.prepend(value)
}
// Создаем новый узел
const node = new Node(value)
// Добавляем ссылку на следующий (новый) узел в хвостовой
this.tail.next = node
// Добавляем ссылку на предыдущий (хвостовой) узел в новый
node.prev = this.tail
// Обновляем хвостовой узел
this.tail = node
return this
}
Методы удаления головного (первого) и хвостового (последнего) узлов:
// Удаляет головной узел
removeHead() {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - удалять нечего
return null
}
// Удаляемый узел - головной
const removed = this.head
// Если головной узел содержит ссылку на следующий
if (this.head.next) {
// �Обновляем головной узел (заменяем на следующий)
this.head = this.head.next
// Обнуляем ссылку головного узла на предыдущий
this.head.prev = null
} else {
// Иначе, обнуляем головной и хвостовой узлы
// (делаем список пустым, поскольку он содержал только один узел)
this.head = null
this.tail = null
}
// Возвращаем удаленный узел
return removed
}
// Удаляет хвостовой узел
removeTail() {
// Если хвостовой узел отсутствует, значит,
if (!this.tail) {
// список пуст -удалять нечего
return null
}
// Удаляемый узел - хвостовой
const removed = this.tail
// Крайний случай: если список состоит из одного узла
if (this.head === this.tail) {
// Обнуляем головной и хвостовой узлы
// (делаем список пустым)
this.head = null
this.tail = null
// Возвращаем удаленный узел
return removed
}
// Обновляем хвостовой узел (заменяем на предыдущий)
this.tail = this.tail.prev
// Обнуляем ссылку хвостового узла на следующий
this.tail.next = null
// Возвращаем удаленный узел
return removed
}
Метод удаления узла по значению:
// Удаляет узел по значению
remove(value) {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - удалять нечего
return null
}
// Удаляемый узел
let removed = null
// Текущий узел (начинаем с головного)
let current = this.head
// Пока есть текущий узел
while (current) {
// Если значения совпадают
if (this.compare.equal(current.value, value)) {
// Обновляем удаляемый узел
removed = current
// Если удаляется головной узел,
if (removed === this.head) {
// обновляем головной узел
this.head = removed.next
// Если новый головной узел имеется,
if (this.head) {
// обнуляем его ссылку на предыдущий узел
this.head.prev = null
}
// Если также удаляется хвостовой узел
// (список содержит только один узел),
if (removed === this.tail) {
// обнуляем хвостовой узел
// (делаем список пустым)
this.tail = null
}
// Иначе, если удаляется хвостовой узел,
} else if (removed === this.tail) {
// обновляем хвостовой узел
this.tail = removed.prev
// Обнуляем ссылку хвостового узла на следующий
this.tail.next = null
} else {
// Предыдущий узел
const prev = removed.prev
// Следующий узел
const next = removed.next
// Обновляем ссылку предыдущего узла на следующий
prev.next = next
// Обновляем ссылку следующего узла на предыдущий
// (закрываем образовавшуюся брешь)
next.prev = prev
}
}
// Переходим к следующему узлу
current = current.next
}
// Возвращаем удаленный узел
return removed
}
Метод поиска узла по значению:
// Ищет узел по значению.
// Принимает искомое значение и функцию поиска
// в виде объекта
find({ value, cb }) {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - искать нечего
return null
}
// Текущий узел (начинаем с головного)
let current = this.head
// Пока есть текущий узел
while (current) {
// Если передана функция, и она удовлетворяется,
if (cb && cb(current.value)) {
// возвращаем текущий узел
return current
}
// Если передано значение, и значения совпадают,
if (value && this.compare.equal(current.value, value)) {
// возвращаем текущий узел
return current
}
// Переходим к следующему узлу
current = current.next
}
// Ничего не найдено
return null
}
Метод инвертирования списка:
// Инвертирует список
reverse() {
// Текущий узел (начинаем с головного)
let current = this.head
// Предыдущий узел
let prev = null
// Следующий узел
let next = null
// Пока есть текущий узел
while (current) {
// Обновляем переменную для следующего узла
next = current.next
// Обновляем переменную для предыдущего узла
prev = current.prev
// Обновляем ссылки текущего узла
current.next = prev
current.prev = next
// Обновляем переменную для предыдущего узла
prev = current
// Переходим к следующему узлу
current = next
}
// Меняем местами головной и хвостовой узлы
this.tail = this.head
// Обновляем головной узел
// (заменяем последним предыдущим - хвостовым)
this.head = prev
return this
}
Напоследок реализуем несколько вспомогательных методов:
// Создает список из массива
fromArray(arr) {
// Перебираем элементы массива и добавляем каждый в конец списка
arr.forEach((value) => this.append(value))
return this
}
// Преобразует список в массив
toArray() {
// Массив узлов
const arr = []
// Текущий узел (начинаем с головного)
let current = this.head
// Пока есть текущий узел
while (current) {
// Добавляем узел в массив
arr.push(current)
// Переходим к следующему узлу
current = current.next
}
// Возвращаем массив
return arr
}
// Возвращает строковое представление списка.
// Принимает кастомную функцию стрингификации
toString(cb) {
// Преобразуем список в массив
return (
this.toArray()
// Перебираем узлы и преобразуем каждый в строку
.map((node) => node.toString(cb))
// Преобразуем массив в строку
.toString()
)
}
Полный код двусвязного списка
import Comparator from '../utils/comparator'
// Узел
export class Node {
constructor(value, next = null, prev = null) {
// Значение
this.value = value
// Ссылка на следующий узел
this.next = next
// Ссылка на предыдущий узел
this.prev = prev
}
// Возвращает строковое представление узла.
// Принимает кастомную функцию стрингификации
toString(cb) {
return cb ? cb(this.value) : `${this.value}`
}
}
// Двусвязный список
export default class DoublyLinkedList {
constructor(fn) {
// Головной (первый) узел
this.head = null
// Хвостовой (последний) узел
this.tail = null
// Функция сравнения узлов
this.compare = new Comparator(fn)
}
// Добавляет значение в начало списка
prepend(value) {
// Создаем новый узел
const node = new Node(value, this.head)
// Если головной узел имеется,
if (this.head) {
// обновляем его ссылку на предыдущий узел
this.head.prev = node
}
// Обновляем головной узел (заменяем на новый)
this.head = node
// Если хвостовой узел отсутствует, значит,
if (!this.tail) {
// головной узел также является хвостовым
// (список был пустым)
this.tail = node
}
// Это обеспечивает возможность вызова методов по цепочке
return this
}
// Добавляет значение в конец списка
append(value) {
// Если головной узел отсутствует,
if (!this.head) {
// добавляем значение в начало списка
return this.prepend(value)
}
// Создаем новый узел
const node = new Node(value)
// Добавляем ссылку на следующий (новый) узел в хвостовой
this.tail.next = node
// Добавляем ссылку на предыдущий (хвостовой) узел в новый
node.prev = this.tail
// Обновляем хвостовой узел
this.tail = node
return this
}
// Удаляет головной узел
removeHead() {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - удалять нечего
return null
}
// Удаляемый узел - головной
const removed = this.head
// Если головной узел содержит ссылку на следующий
if (this.head.next) {
// Обновляем головной узел
this.head = this.head.next
// Обнуляем ссылку головного узла на предыдущий
this.head.prev = null
} else {
// Иначе, обнуляем головной и хвостовой узлы
// (делаем список пустым, поскольку он содержал только один узел)
this.head = null
this.tail = null
}
// Возвращаем удаленный узел
return removed
}
// Удаляет хвостовой узел
removeTail() {
// Если хвостовой узел отсутствует, значит,
if (!this.tail) {
// список пуст -удалять нечего
return null
}
// Удаляемый узел - хвостовой
const removed = this.tail
// Крайний случай: если список состоит из одного узла
if (this.head === this.tail) {
// Обнуляем головной и хвостовой узлы
// (делаем список пустым)
this.head = null
this.tail = null
// Возвращаем удаленный узел
return removed
}
// Обновляем хвостовой узел (заменяем на предыдущий)
this.tail = this.tail.prev
// Обнуляем ссылку хвостового узла на следующий
this.tail.next = null
// Возвращаем удаленный узел
return removed
}
// Удаляет узел по значению
remove(value) {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - удалять нечего
return null
}
// Удаляемый узел
let removed = null
// Текущий узел (начинаем с головного)
let current = this.head
// Пока есть текущий узел
while (current) {
// Если значения совпадают
if (this.compare.equal(current.value, value)) {
// Обновляем уда�ляемый узел
removed = current
// Если удаляется головной узел,
if (removed === this.head) {
// обновляем головной узел
this.head = removed.next
// Если новый головной узел имеется,
if (this.head) {
// обнуляем его ссылку на предыдущий узел
this.head.prev = null
}
// Если также удаляется хвостовой узел
// (список содержит только один узел),
if (removed === this.tail) {
// обнуляем хвостовой узел
// (делаем список пустым)
this.tail = null
}
// Иначе, если удаляется хвостовой узел,
} else if (removed === this.tail) {
// обновляем хвостовой узел
this.tail = removed.prev
// Обнуляем ссылку хвостового узла на следующий
this.tail.next = null
} else {
// Предыдущий узел
const prev = removed.prev
// Следующий узел
const next = removed.next
// Обновляем ссылку предыдущего узла на следующий
prev.next = next
// Обновляем ссылку следующего узла на предыдущий
// (закрываем образовавшуюся брешь)
next.prev = prev
}
}
// Переходим к следующему узлу
current = current.next
}
// Возвращаем удаленный узел
return removed
}
// Ищет узел по значению.
// Принимает искомое значение и функцию поиска
// в виде объекта
find({ value, cb }) {
// Если головной узел отсутствует, значит,
if (!this.head) {
// список пуст - искать нечего
return null
}
// Текущий узел (начинаем с головного)
let current = this.head
// Пока есть текущий узел
while (current) {
// Если передана функция, и она удовлетворяется,
if (cb && cb(current.value)) {
// возвращаем текущий узел
return current
}
// Если передано значение, и значения совпадают,
if (value && this.compare.equal(current.value, value)) {
// возвращаем текущий узел
return current
}
// Переходим к следующему узлу
current = current.next
}
// Ничего не найдено
return null
}
// Инвертирует список
reverse() {
// Текущий узел (начинаем с головного)
let current = this.head
// Предыдущий узел
let prev = null
// Следующий узел
let next = null
// Пока есть текущий узел
while (current) {
// Обновляем переменную для следующего узла
next = current.next
// Обновляем переменную для предыдущего узла
prev = current.prev
// Обновляем ссылки текущего узла
current.next = prev
current.prev = next
// Обновляем переменную �для предыдущего узла
prev = current
// Переходим к следующему узлу
current = next
}
// Меняем местами головной и хвостовой узлы
this.tail = this.head
// Обновляем головной узел
// (заменяем последним предыдущим - хвостовым)
this.head = prev
return this
}
// Создает список из массива
fromArray(arr) {
// Перебираем элементы массива и добавляем каждый в конец списка
arr.forEach((value) => this.append(value))
return this
}
// Преобразует список в массив
toArray() {
// Массив узлов
const arr = []
// Текущий узел (начинаем с головного)
let current = this.head
// Пока есть текущий узел
while (current) {
// Добавляем узел в массив
arr.push(current)
// Переходим к следующему узлу
current = current.next
}
// Возвращаем массив
return arr
}
// Возвращает строковое представление списка.
// Принимает кастомную функцию стрингификации
toString(cb) {
// Преобразуем список в массив
return (
this.toArray()
// Перебираем узлы и преобразуем каждый в строку
.map((node) => node.toString(cb))
// Преобразуем массив в строку
.toString()
)
}
}
Тестирование
Проверим, что наш двусвязный список работает, как ожидается.
Начнем с узла:
// data-structures/__tests__/doubly-linked-list.test.js
import DoublyLinkedList, { Node } from '../doubly-linked-list'
describe('DoublyLinkedListNode', () => {
it('должен создать узел с указанным значением', () => {
const node = new Node(1)
expect(node.value).toBe(1)
expect(node.next).toBeNull()
expect(node.prev).toBeNull()
})
it('должен создать узел с объектом в качестве значения', () => {
const nodeValue = { value: 1, key: 'test' }
const node = new Node(nodeValue)
expect(node.value.value).toBe(1)
expect(node.value.key).toBe('test')
expect(node.next).toBeNull()
expect(node.prev).toBeNull()
})
it('должен соединить узлы вместе', () => {
const node2 = new Node(2)
const node1 = new Node(1, node2)
const node3 = new Node(10, node1, node2)
expect(node1.next).toBeDefined()
expect(node1.prev).toBeNull()
expect(node2.next).toBeNull()
expect(node2.prev).toBeNull()
expect(node3.next).toBeDefined()
expect(node3.prev).toBeDefined()
expect(node1.value).toBe(1)
expect(node1.next.value).toBe(2)
expect(node3.next.value).toBe(1)
expect(node3.prev.value).toBe(2)
})
it('должен преобразовать узел в строку', () => {
const node = new Node(1)
expect(node.toString()).toBe('1')
node.value = 'string value'
expect(node.toString()).toBe('string value')
})
it('должен преобразовать узел в строку с помощью кастомной функции', () => {
const nodeValue = { value: 1, key: 'test' }
const node = new Node(nodeValue)
const toStringCallback = (value) =>
`value: ${value.value}, key: ${value.key}`
expect(node.toString(toStringCallback)).toBe('value: 1, key: test')
})
})
Теперь сам список
describe('DoublyLinkedList', () => {
it('должен создать пустой двусвязный список', () => {
const linkedList = new DoublyLinkedList()
expect(linkedList.toString()).toBe('')
})
it('должен добавить узлы в конец списка', () => {
const linkedList = new DoublyLinkedList()
expect(linkedList.head).toBeNull()
expect(linkedList.tail).toBeNull()
linkedList.append(1)
linkedList.append(2)
expect(linkedList.head.next.value).toBe(2)
expect(linkedList.tail.prev.value).toBe(1)
expect(linkedList.toString()).toBe('1,2')
})
it('должен добавить узлы в начало списка', () => {
const linkedList = new DoublyLinkedList()
linkedList.prepend(2)
expect(linkedList.head.toString()).toBe('2')
expect(linkedList.tail.toString()).toBe('2')
linkedList.append(1)
linkedList.prepend(3)
expect(linkedList.head.next.next.prev).toBe(linkedList.head.next)
expect(linkedList.tail.prev.next).toBe(linkedList.tail)
expect(linkedList.tail.prev.value).toBe(2)
expect(linkedList.toString()).toBe('3,2,1')
})
it('должен создать список из массива', () => {
const linkedList = new DoublyLinkedList()
linkedList.fromArray([1, 1, 2, 3, 3, 3, 4, 5])
expect(linkedList.toString()).toBe('1,1,2,3,3,3,4,5')
})
it('должен удалить узлы по значениям', () => {
const linkedList = new DoublyLinkedList()
expect(linkedList.remove(5)).toBeNull()
linkedList.append(1)
linkedList.append(1)
linkedList.append(2)
linkedList.append(3)
linkedList.append(3)
linkedList.append(3)
linkedList.append(4)
linkedList.append(5)
expect(linkedList.head.toString()).toBe('1')
expect(linkedList.tail.toString()).toBe('5')
const removedNode = linkedList.remove(3)
expect(removedNode.value).toBe(3)
expect(linkedList.tail.prev.prev.value).toBe(2)
expect(linkedList.toString()).toBe('1,1,2,4,5')
linkedList.remove(3)
expect(linkedList.toString()).toBe('1,1,2,4,5')
linkedList.remove(1)
expect(linkedList.toString()).toBe('2,4,5')
expect(linkedList.head.toString()).toBe('2')
expect(linkedList.head.next.next).toBe(linkedList.tail)
expect(linkedList.tail.prev.prev).toBe(linkedList.head)
expect(linkedList.tail.toString()).toBe('5')
linkedList.remove(5)
expect(linkedList.toString()).toBe('2,4')
expect(linkedList.head.toString()).toBe('2')
expect(linkedList.tail.toString()).toBe('4')
linkedList.remove(4)
expect(linkedList.toString()).toBe('2')
expect(linkedList.head.toString()).toBe('2')
expect(linkedList.tail.toString()).toBe('2')
expect(linkedList.head).toBe(linkedList.tail)
linkedList.remove(2)
expect(linkedList.toString()).toBe('')
})
it('должен удалить хвостовые узлы', () => {
const linkedList = new DoublyLinkedList()
expect(linkedList.removeTail()).toBeNull()
linkedList.append(1)
linkedList.append(2)
linkedList.append(3)
expect(linkedList.head.toString()).toBe('1')
expect(linkedList.tail.toString()).toBe('3')
const removedNode1 = linkedList.removeTail()
expect(removedNode1.value).toBe(3)
expect(linkedList.toString()).toBe('1,2')
expect(linkedList.head.toString()).toBe('1')
expect(linkedList.tail.toString()).toBe('2')
const removedNode2 = linkedList.removeTail()
expect(removedNode2.value).toBe(2)
expect(linkedList.toString()).toBe('1')
expect(linkedList.head.toString()).toBe('1')
expect(linkedList.tail.toString()).toBe('1')
const removedNode3 = linkedList.removeTail()
expect(removedNode3.value).toBe(1)
expect(linkedList.toString()).toBe('')
expect(linkedList.head).toBeNull()
expect(linkedList.tail).toBeNull()
})
it('должен удалить головные узлы', () => {
const linkedList = new DoublyLinkedList()
expect(linkedList.removeHead()).toBeNull()
linkedList.append(1)
linkedList.append(2)
expect(linkedList.head.toString()).toBe('1')
expect(linkedList.tail.toString()).toBe('2')
const removedNode1 = linkedList.removeHead()
expect(removedNode1.value).toBe(1)
expect(linkedList.head.prev).toBeNull()
expect(linkedList.toString()).toBe('2')
expect(linkedList.head.toString()).toBe('2')
expect(linkedList.tail.toString()).toBe('2')
const removedNode2 = linkedList.removeHead()
expect(removedNode2.value).toBe(2)
expect(linkedList.toString()).toBe('')
expect(linkedList.head).toBeNull()
expect(linkedList.tail).toBeNull()
})
it('должен добавить в список значения в виде объектов', () => {
const linkedList = new DoublyLinkedList()
const nodeValue1 = { value: 1, key: 'key1' }
const nodeValue2 = { value: 2, key: 'key2' }
linkedList.append(nodeValue1).prepend(nodeValue2)
const nodeStringifier = (value) => `${value.key}:${value.value}`
expect(linkedList.toString(nodeStringifier)).toBe('key2:2,key1:1')
})
it('должен найти узлы по значениям', () => {
const linkedList = new DoublyLinkedList()
expect(linkedList.find({ value: 5 })).toBeNull()
linkedList.append(1)
expect(linkedList.find({ value: 1 })).toBeDefined()
linkedList.append(2).append(3)
const node = linkedList.find({ value: 2 })
expect(node.value).toBe(2)
expect(linkedList.find({ value: 5 })).toBeNull()
})
it('должен найти узлы с помощью кастомной функции', () => {
const linkedList = new DoublyLinkedList()
linkedList
.append({ value: 1, key: 'test1' })
.append({ value: 2, key: 'test2' })
.append({ value: 3, key: 'test3' })
const node = linkedList.find({ cb: (value) => value.key === 'test2' })
expect(node).toBeDefined()
expect(node.value.value).toBe(2)
expect(node.value.key).toBe('test2')
expect(linkedList.find({ cb: (value) => value.key === 'test5' })).toBeNull()
})
it('должен найти узлы с помощью кастомной функции сравнения', () => {
const comparatorFunction = (a, b) => {
if (a.customValue === b.customValue) {
return 0
}
return a.customValue < b.customValue ? -1 : 1
}
const linkedList = new DoublyLinkedList(comparatorFunction)
linkedList
.append({ value: 1, customValue: 'test1' })
.append({ value: 2, customValue: 'test2' })
.append({ value: 3, customValue: 'test3' })
const node = linkedList.find({
value: { value: 2, customValue: 'test2' },
})
expect(node).toBeDefined()
expect(node.value.value).toBe(2)
expect(node.value.customValue).toBe('test2')
expect(linkedList.find({ value: 2, customValue: 'test5' })).toBeNull()
})
it('должен инвертировать список', () => {
const linkedList = new DoublyLinkedList()
// Добавляем тестовые значения в список
linkedList.append(1).append(2).append(3).append(4)
expect(linkedList.toString()).toBe('1,2,3,4')
expect(linkedList.head.value).toBe(1)
expect(linkedList.tail.value).toBe(4)
// Инвертируем список
linkedList.reverse()
expect(linkedList.toString()).toBe('4,3,2,1')
expect(linkedList.head.prev).toBeNull()
expect(linkedList.head.value).toBe(4)
expect(linkedList.head.next.value).toBe(3)
expect(linkedList.head.next.next.value).toBe(2)
expect(linkedList.head.next.next.next.value).toBe(1)
expect(linkedList.tail.next).toBeNull()
expect(linkedList.tail.value).toBe(1)
expect(linkedList.tail.prev.value).toBe(2)
expect(linkedList.tail.prev.prev.value).toBe(3)
expect(linkedList.tail.prev.prev.prev.value).toBe(4)
// Инвертируем список обратно в начальное состояние
linkedList.reverse()
expect(linkedList.toString()).toBe('1,2,3,4')
expect(linkedList.head.prev).toBeNull()
expect(linkedList.head.value).toBe(1)
expect(linkedList.head.next.value).toBe(2)
expect(linkedList.head.next.next.value).toBe(3)
expect(linkedList.head.next.next.next.value).toBe(4)
expect(linkedList.tail.next).toBeNull()
expect(linkedList.tail.value).toBe(4)
expect(linkedList.tail.prev.value).toBe(3)
expect(linkedList.tail.prev.prev.value).toBe(2)
expect(linkedList.tail.prev.prev.prev.value).toBe(1)
})
})
Запускаем тесты:
npm run test ./data-structures/__tests__/doubly-linked-list
Результат:

Очередь
Описание
Очередь (queue) - это динам�ическая структура данных, в которой элементы хранятся в порядке их добавления. Она является примером линейной структуры или последовательной коллекции. Новые элементы добавляются в конец очереди (enqueue). Удаление элементов выполняется с начала очереди (dequeue). Таким образом, очередь реализует принцип "первым вошел - первым вышел" (first in - first out, FIFO). Кроме enqueue и dequeue, часто также реализуется операция чтения значения головного узла без его удаления (peek).
Иллюстрацией рассматриваемой структуры данных может служить любая очередь в обычной жизни, например, из тех, кто только спросить :D

Реализация
Для реализации очереди мы воспользуемся связным списком (см. раздел 1).
Говорить тут особо не о чем, так что привожу сразу весь код:
// data-structures/queue.js
// Импортируем конструктор связного списка
import LinkedList from './linked-list'
// Очередь
export default class Queue {
constructor() {
// Создаем связный список
this.list = new LinkedList()
}
// Проверяет, является ли очередь пустой
isEmpty() {
return !this.list.head
}
// Возвращает значение первого узла без его удаления
peek() {
if (this.isEmpty()) {
return null
}
return this.list.head.value
}
// Добавляет элемент в конец очереди
enqueue(value) {
this.list.append(value)
}
// Удаляет первый узел и возвращает его значение
dequeue() {
const removedHead = this.list.removeHead()
return removedHead?.value || null
}
// Преобразует очередь в строку.
// Принимает кастомную функцию стрингификации
toString(cb) {
return this.list.toString(cb)
}
// Преобразует очередь в массив значений
toArray() {
return this.list.toArray().map((node) => node.value)
}
}
Тестирование
Проверяем, что наша очередь работает, как ожидается:
// data-structures/__tests__/queue.test.js
import Queue from '../queue'
describe('Queue', () => {
it('должен создать пустую очередь', () => {
const queue = new Queue()
expect(queue).not.toBeNull()
expect(queue.linkedList).not.toBeNull()
})
it('должен добавить значения в очередь', () => {
const queue = new Queue()
queue.enqueue(1)
queue.enqueue(2)
expect(queue.toString()).toBe('1,2')
})
it('должен добавить/удалить объекты в/из очереди', () => {
const queue = new Queue()
queue.enqueue({ value: 'test1', key: 'key1' })
queue.enqueue({ value: 'test2', key: 'key2' })
const stringifier = (value) => `${value.key}:${value.value}`
expect(queue.toString(stringifier)).toBe('key1:test1,key2:test2')
expect(queue.dequeue().value).toBe('test1')
expect(queue.dequeue().value).toBe('test2')
})
it('должен извлечь значения из очереди без удаления и с удалением соответствующих узлов', () => {
const queue = new Queue()
expect(queue.peek()).toBeNull()
queue.enqueue(1)
queue.enqueue(2)
expect(queue.peek()).toBe(1)
expect(queue.peek()).toBe(1)
})
it('должен проверить пустоту очереди', () => {
const queue = new Queue()
expect(queue.isEmpty()).toBe(true)
queue.enqueue(1)
expect(queue.isEmpty()).toBe(false)
})
it('должен удалять элементы из очереди в порядке FIFO', () => {
const queue = new Queue()
queue.enqueue(1)
queue.enqueue(2)
expect(queue.dequeue()).toBe(1)
expect(queue.dequeue()).toBe(2)
expect(queue.dequeue()).toBeNull()
expect(queue.isEmpty()).toBe(true)
})
})
Запускаем тесты:
npm run test ./data-structures/__tests__/queue
Результат:

Стек
Описание
Стек (stack) - это динамическая структура данных, в которой элементы хранятся в порядке, обратному порядку их добавления. Она, как и очередь, является примером линейной структуры или последовательной коллекции. Новые элементы добавляются в начало стека (push). Удаление элементов также выполняется с начала стека (pop). Таким образом, стек реализует принцип "последним вошел - первым вышел" (last in - first out, LIFO). Кроме push и pop, часто также реализуется операция чтения значения головного узла без его удаления (peek).
Иллюстрацией рассматриваемой структуры данных может служить стопка книг: для того, чтобы взять вторую книгу сверху, нужно сначала снять верхнюю.

Реализация
Для реализации стека мы также воспользуемся связным списком (см. раздел 1).
Привожу сразу весь код:
// data-structures/stack.js
// Импортируем конструктор связного списка
import LinkedList from './linked-list'
// Стек
export default class Stack {
constructor() {
// Создаем связный список
this.list = new LinkedList()
}
// Проверяет, является ли стек пустым
isEmpty() {
return !this.list.head
}
// Возвращает значение первого узла без его удаления
peek() {
if (this.isEmpty()) {
return null
}
return this.list.head.value
}
// Добавляет элемент в начало стека
push(value) {
this.list.prepend(value)
}
// Удаляет первый узел и возвращает его значение
pop() {
const removedHead = this.list.removeHead()
return removedHead?.value || null
}
// Преобразует стек в строку
toString(cb) {
return this.list.toString(cb)
}
// Преобразует стек в массив значений
toArray() {
return this.list.toArray().map((node) => node.value)
}
}
Тестирование
Проверяем, что наш стек работает, как ожидается:
// data-structures/__tests__/stack.test.js
import Stack from '../stack'
describe('Stack', () => {
it('должен создать пустой стек', () => {
const stack = new Stack()
expect(stack).not.toBeNull()
expect(stack.linkedList).not.toBeNull()
})
it('должен добавить значения в стек', () => {
const stack = new Stack()
stack.push(1)
stack.push(2)
expect(stack.toString()).toBe('2,1')
})
it('должен проверить пустоту стека', () => {
const stack = new Stack()
expect(stack.isEmpty()).toBe(true)
stack.push(1)
expect(stack.isEmpty()).toBe(false)
})
it('должен извлечь значения из стека без удаления узлов', () => {
const stack = new Stack()
expect(stack.peek()).toBeNull()
stack.push(1)
stack.push(2)
expect(stack.peek()).toBe(2)
expect(stack.peek()).toBe(2)
})
it('должен извлечь значения из стека с удалением узлов', () => {
const stack = new Stack()
stack.push(1)
stack.push(2)
expect(stack.pop()).toBe(2)
expect(stack.pop()).toBe(1)
expect(stack.pop()).toBeNull()
expect(stack.isEmpty()).toBe(true)
})
it('должен добавить/удалить объекты в/из стека', () => {
const stack = new Stack()
stack.push({ value: 'test1', key: 'key1' })
stack.push({ value: 'test2', key: 'key2' })
const stringifier = (value) => `${value.key}:${value.value}`
expect(stack.toString(stringifier)).toBe('key2:test2,key1:test1')
expect(stack.pop().value).toBe('test2')
expect(stack.pop().value).toBe('test1')
})
it('должен преобразовать стек в массив', () => {
const stack = new Stack()
expect(stack.peek()).toBeNull()
stack.push(1)
stack.push(2)
stack.push(3)
expect(stack.toArray()).toEqual([3, 2, 1])
})
})
Запускаем тесты:
npm run test ./data-structures/__tests__/stack
Результат:

Хэш-таблица
Описание
Хэш-таблица (hash table) - это структура данных, которая реализует абстрактный тип данных "ассоциативный массив" и позволяет хранить пары "ключ-значение". Хэш-таблица использует так называемую хэш-функцию (hash function), которая принимает ключ и возвращает индекс массива, по которому будет храниться значение (см. хорошее видео про хэширование). Пример хэш-таблицы, в которой ключом выступает имя человека, а значением адрес его электронной почты:

В идеале хэш-функция должна генерировать уникальный индекс для каждого ключа. Однако реальные хэш-таблицы используют несовершенные хэш-функции, генерирующие одинаковые индексы для разных ключей. Такие ситуации называются коллизиями (collisions). Существует несколько способов их решения, наиболее популярными из которых являются: хэш-таблица с цепочками и хэш-таблица с открытой адресацией.
Метод цепочек подразумевает хранение значений, соответствующих одному индексу в виде связного списка (linked list) (см. часть 1, раздел 1):

Метод открытой адресации помещает значение по совпадающему индексу в первую свободную ячейку:

Реализация
Приступаем к реализации хэш-таблицы:
// data-structures/hash-table.js
// Импортируем конструктор связного списка
// (мы будем использовать метод цепочек для разрешения коллизий)
import LinkedList from './linked-list'
// Дефолтный размер таблицы
// (в реальности размер будет намного больше)
const defaultHashTableSize = 32
// Хэш-таблица
export default class HashTable {
constructor(size = defaultHashTableSize) {
// Создаем таблицу указанного размера и
// заполняем ее пустыми связными списками
this.buckets = new Array(size).fill(null).map(() => new LinkedList())
// Хранилище ключей
this.keys = {}
}
}
Реализуем простейшую хэш-функцию:
// Преобразует ключ в хэшированное значение
// (хэш-функция)
hash(key) {
// Для простоты в качестве хэша используется сумма кодов символов ключа
// https://developer.mozilla.org/ru/docs/Web/JavaScript/Reference/Global_Objects/String/charCodeAt
const hash = [...key].reduce((acc, char) => acc + char.charCodeAt(0), 0)
// Хэш (индекс) не должен превышать размера таблицы
return hash % this.buckets.length
}
Метод установки значения по ключу:
// Устанавливает значение по ключу
set(key, value) {
// Хэшируем ключ
// (получаем индекс массива)
const index = this.hash(key)
// Сохраняем хэш по ключу
this.keys[key] = index
// Извлекаем нужный список
const bucket = this.buckets[index]
// Извлекаем узел
// (значением узла является объект)
const node = bucket.find({ cb: (value) => value.key === key })
// Если узел не найден
if (!node) {
// Добавляем новый узел
bucket.append({ key, value })
} else {
// Иначе, обновляем значение узла
node.value.value = value
}
}
Метод удаления значения по ключу:
// Удаляет значение по ключу
remove(key) {
// Хэшируем ключ
const index = this.hash(key)
// Удаляем хэш по ключу
delete this.keys[key]
// Извлекаем нужный список
const bucket = this.buckets[index]
// Извлекаем узел
const node = bucket.find({ cb: (value) => value.key === key })
// Возвращаем удаленный узел или `null`,
// если узел отсутствует
return node ? bucket.remove(node.value) : null
}
Метод извлечения значения по ключу:
// Возвращает значение по ключу
get(key) {
// Хэшируем ключ
const index = this.hash(key)
// Извлекаем нужный список
const bucket = this.buckets[index]
// Извлекаем узел
const node = bucket.find({ cb: (value) => value.key === key })
// Возвращаем значение узла или `null`,
// если узел отсутствует
return node ? node.value.value : null
}
Напоследок реализуем несколько вспомогательных методов:
// Определяет наличие ключа
has(key) {
// https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Object/hasOwn
return Object.hasOwn(this.keys, key)
}
// Возвращает все ключи
getKeys() {
return Object.keys(this.keys)
}
// Возвращает все значения
getValues() {
// Перебираем списки и возвращаем значения всех узлов
return this.buckets.reduce((acc, bucket) => {
return acc.concat(
// Метод `toArray` преобразует связный список в массив
bucket.toArray().map((node) => node.value.value),
)
}, [])
}
Полный код хэш-таблицы
// Импортируем конструктор связного списка
// (мы будем использовать метод цепочек для разрешения коллизий)
import LinkedList from './linked-list'
// Дефолтный размер таблицы
// (в реальности размер будет намного больше)
const defaultSize = 32
// Хэш-таблица
export default class HashTable {
constructor(size = defaultSize) {
// Создаем таблицу указанного размера и
// заполняем ее пустыми связными списками
this.buckets = new Array(size).fill(null).map(() => new LinkedList())
// Хранилище ключей
this.keys = {}
}
// Преобразует ключ в хэшированное значение
// (хэш-функция)
hash(key) {
// Для простоты в качестве хэша используется сумма кодов символов ключа
// https://developer.mozilla.org/ru/docs/Web/JavaScript/Reference/Global_Objects/String/charCodeAt
const hash = [...key].reduce((acc, char) => acc + char.charCodeAt(0), 0)
// Хэшированное значение не должно превышать размера таблицы
return hash % this.buckets.length
}
// Устанавливает значение по ключу
set(key, value) {
// Хэшируем ключ
// (получаем индекс массива)
const index = this.hash(key)
// Сохраняем хэш по ключу
this.keys[key] = index
// Извлекаем нужный список
const bucket = this.buckets[index]
// Извлекаем узел
// (значением узла является объект)
const node = bucket.find({ cb: (value) => value.key === key })
// Если узел не найден
if (!node) {
// Добавляем новый узел
bucket.append({ key, value })
} else {
// Иначе, обновляем значение узла
node.value.value = value
}
}
// Удаляет значение по ключу
remove(key) {
// Хэшируем ключ
const index = this.hash(key)
// Удаляем хэш по ключу
delete this.keys[key]
// Извлекаем нужный список
const bucket = this.buckets[index]
// Извлекаем узел
const node = bucket.find({ cb: (value) => value.key === key })
// Возвращаем удаленный узел или `null`,
// если узел отсутствует
return node ? bucket.remove(node.value) : null
}
// Возвращает значение по ключу
get(key) {
// Хэшируем ключ
const index = this.hash(key)
// Извлекаем нужный список
const bucket = this.buckets[index]
// Извлекаем узел
const node = bucket.find({ cb: (value) => value.key === key })
// Возвращаем значение узла или `null`,
// если узел отсутствует
return node ? node.value.value : null
}
// Определяет наличие ключа
has(key) {
// https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Object/hasOwn
return Object.hasOwn(this.keys, key)
}
// Возвращает все ключи
getKeys() {
return Object.keys(this.keys)
}
// Возвращает все значения
getValues() {
// Перебираем списки и возвращаем значения всех узлов
return this.buckets.reduce((acc, bucket) => {
return acc.concat(
// Метод `toArray` преобразует связный список в массив
bucket.toArray().map((node) => node.value.value),
)
}, [])
}
}
Тестирование
Проверяем, что наша хэш-таблица работает, как ожидается
// data-structures/__tests__/hash-table.test.js
import HashTable from '../hash-table'
describe('HashTable', () => {
it('должен создать хэш-таблицы указанного размера', () => {
const defaultHashTable = new HashTable()
expect(defaultHashTable.buckets.length).toBe(32)
const biggerHashTable = new HashTable(64)
expect(biggerHashTable.buckets.length).toBe(64)
})
it('должен генерировать правильный хэш для ключей', () => {
const hashTable = new HashTable()
expect(hashTable.hash('a')).toBe(1)
expect(hashTable.hash('b')).toBe(2)
expect(hashTable.hash('abc')).toBe(6)
})
it('должен устанавливать, читать и удалять значения с коллизиями', () => {
const hashTable = new HashTable(3)
expect(hashTable.hash('a')).toBe(1)
expect(hashTable.hash('b')).toBe(2)
expect(hashTable.hash('c')).toBe(0)
expect(hashTable.hash('d')).toBe(1)
hashTable.set('a', 'sky-old')
hashTable.set('a', 'sky')
hashTable.set('b', 'sea')
hashTable.set('c', 'earth')
hashTable.set('d', 'ocean')
expect(hashTable.has('x')).toBe(false)
expect(hashTable.has('b')).toBe(true)
expect(hashTable.has('c')).toBe(true)
const stringifier = (value) => `${value.key}:${value.value}`
expect(hashTable.buckets[0].toString(stringifier)).toBe('c:earth')
expect(hashTable.buckets[1].toString(stringifier)).toBe('a:sky,d:ocean')
expect(hashTable.buckets[2].toString(stringifier)).toBe('b:sea')
expect(hashTable.get('a')).toBe('sky')
expect(hashTable.get('d')).toBe('ocean')
expect(hashTable.get('x')).toBeNull()
hashTable.remove('a')
expect(hashTable.remove('not-existing')).toBeNull()
expect(hashTable.get('a')).toBeNull()
expect(hashTable.get('d')).toBe('ocean')
hashTable.set('d', 'ocean-new')
expect(hashTable.get('d')).toBe('ocean-new')
})
it('должен добавить в таблицу объекты', () => {
const hashTable = new HashTable()
hashTable.set('objectKey', { prop1: 'a', prop2: 'b' })
const object = hashTable.get('objectKey')
expect(object).toBeDefined()
expect(object.prop1).toBe('a')
expect(object.prop2).toBe('b')
})
it('должен отслеживать актуальные ключи', () => {
const hashTable = new HashTable(3)
hashTable.set('a', 'sky-old')
hashTable.set('a', 'sky')
hashTable.set('b', 'sea')
hashTable.set('c', 'earth')
hashTable.set('d', 'ocean')
expect(hashTable.getKeys()).toEqual(['a', 'b', 'c', 'd'])
expect(hashTable.has('a')).toBe(true)
expect(hashTable.has('x')).toBe(false)
hashTable.remove('a')
expect(hashTable.has('a')).toBe(false)
expect(hashTable.has('b')).toBe(true)
expect(hashTable.has('x')).toBe(false)
})
it('должен вернуть все значения', () => {
const hashTable = new HashTable(3)
hashTable.set('a', 'alpha')
hashTable.set('b', 'beta')
hashTable.set('c', 'gamma')
expect(hashTable.getValues()).toEqual(['gamma', 'alpha', 'beta'])
})
it('должен вернуть все значения пустой таблицы', () => {
const hashTable = new HashTable()
expect(hashTable.getValues()).toEqual([])
})
it('должен вернуть все значения при наличии коллизий', () => {
const hashTable = new HashTable(3)
// Ключи `ab` и `ba` в текущей реализации будут иметь одинаковый хэш.
// Нужно убедиться в сериализации нескольких значений одного списка
hashTable.set('ab', 'one')
hashTable.set('ba', 'two')
hashTable.set('ac', 'three')
expect(hashTable.getValues()).toEqual(['one', 'two', 'three'])
})
})
Запускаем тесты:
npm run test ./data-structures/__tests__/hash-table
Результат:

Отлично! Двигаемся дальше.
Куча
Описание
Куча (heap) - это специализированная структура данных типа "дерево" (tree), которая удовлетворяет свойству кучи: если B является узлом-потомком узла A, то k(A) >= k(B), где k(X) - ключ (идентификатор) узла. Из этого следует, что элемент с наибольшим значением ключа всегда является корневым узлом (root node) кучи, поэтому такие кучи называют max-кучами (max heaps):

Приведенную max-кучу можно представить в виде массива следующим образом:

Если дерево перевернуть, то корневым узлом всегда будет элемент с наименьшим значением. Такие кучи называют min-кучами:

Не существует никаких ограничений относительно того, сколько узлов-потомков имеет каждый узел кучи, хотя на практике их число обычно не более двух (такие кучи называют "двоичными" или "бинарными" (binary)). Куча является максимально эффективной реализацией абстрактного типа данных, который называется "очередью с приоритетом" (см. следующий раздел). Кучи имеют решающее значение в некоторых эффективных алгоритмах на графах, таких, как алгоритм Дейкстры на d-кучах и сортировка методом пирамиды.
Интерактивную визуализации кучи можно посмотреть здесь.
Сложность
Временная сложность кучи зависит от ее типа.
| Тип кучи | find-max | delete-max | insert | increase-key | meld |
|---|---|---|---|---|---|
| Binary | Θ(1) | Θ(log n) | O(log n) | O(log n) | Θ(n) |
| Leftist | Θ(1) | Θ(log n) | Θ(log n) | O(log n) | Θ(log n) |
| Binomial | Θ(1) | Θ(log n) | Θ(1) | O(log n) | O(log n) |
| Fibonacci | Θ(1) | Θ(log n) | Θ(1) | Θ(1) | Θ(1) |
| Pairing | Θ(1) | Θ(log n) | Θ(1) | o(log n) | Θ(1) |
| Brodal | Θ(1) | Θ(log n) | Θ(1) | Θ(1) | Θ(1) |
| Rank-pairing | Θ(1) | Θ(log n) | Θ(1) | Θ(1) | Θ(1) |
| Strict Fibonacci | Θ(1) | Θ(log n) | Θ(1) | Θ(1) | Θ(1) |
| 2-3 heap | O(log n) | O(log n) | O(log n) | Θ(1) | ? |
Где:
- find-max (или find-min): поиск максимального значения в max-куче или минимального значения в min-куче, соответственно (похоже на peek в очереди или стеке)
- delete-max (or delete-min): удаление корневого узла
- insert: добавление в кучу нового значения (похоже на push в стеке или enqueue в очереди)
- increase-key или decrease-key: обновление значения узла
- meld: объединение 2 куч в 1 с уничтожением оригиналов
Реализация
В рамках этой статьи мы рассмотрим реализацию только бинарной кучи.
Начнем с реализации родительского (или супер, или абстрактного) класса для min- и max-куч. Конструктор этого класса будет выглядеть следующим образом:
// data-structures/heap/index.js
// Импортируем конструктор функции сравнения узлов
import Comparator from '../../utils/comparator'
// Родительский класс для min- и max-куч
export default class Heap {
constructor(fn) {
// Кучи должны создаваться с помощью соответствующих подклассов
if (new.target === Heap) {
throw new TypeError('Кучу нельзя создавать напрямую!')
}
// Представление кучи в виде массива
this.heapContainer = []
// Функция сравнения элементов
this.compare = new Comparator(fn)
}
}
Реализуем несколько вспомогательных методов:
// Возвращает индекс левого потомка
getLeftChildIndex(parentIndex) {
return 2 * parentIndex + 1
}
// Возвращает индекс правого потомка
getRightChildIndex(parentIndex) {
return 2 * parentIndex + 2
}
// Возвращает индекс предка
getParentIndex(childIndex) {
return Math.floor((childIndex - 1) / 2)
}
// Проверяет наличие предка
hasParent(childIndex) {
return this.getParentIndex(childIndex) >= 0
}
// Проверяет наличие левого потомка
hasLeftChild(parentIndex) {
return this.getLeftChildIndex(parentIndex) < this.heapContainer.length
}
// Проверяет наличие правого потомка
hasRightChild(parentIndex) {
return this.getRightChildIndex(parentIndex) < this.heapContainer.length
}
// Возвращает левого потомка
leftChild(parentIndex) {
return this.heapContainer[this.getLeftChildIndex(parentIndex)]
}
// Возвращает правого потомка
rightChild(parentIndex) {
return this.heapContainer[this.getRightChildIndex(parentIndex)]
}
// Возвращает предка
parent(childIndex) {
return this.heapContainer[this.getParentIndex(childIndex)]
}
// Определяет пустоту кучи
isEmpty() {
return this.heapContainer.length === 0
}
// Возвращает строковое представление кучи
toString() {
return this.heapContainer.toString()
}
Методы получения ссылки на корневой элемент кучи и самого корневого элемента:
// Возвращает ссылку на корневой элемент кучи
// (наименьший для min-кучи, наибольший для max-кучи;
// элемент не удаляется)
peek() {
if (this.isEmpty()) {
return null
}
return this.heapContainer[0]
}
// Удаляет и возвращает корневой элемент кучи
poll() {
if (this.isEmpty()) {
return null
}
if (this.heapContainer.length === 1) {
return this.heapContainer.pop()
}
const item = this.heapContainer[0]
// Перемещаем последний элемент в начало
this.heapContainer[0] = this.heapContainer.pop()
// Просеиваем кучу вниз
this.heapifyDown()
// Возвращаем удаленный элемент
return item
}
Методы добавления и удаления элементов:
// Добавляет элемент в кучу
add(item) {
// Добавляем новый элемент в конец кучи
this.heapContainer.push(item)
// Просеиваем кучу вверх
this.heapifyUp()
return this
}
// Удаляет элемент из кучи.
// Принимает элемент и кастомную функцию сравнения элементов
remove(item, comparator = this.compare) {
// Определяем количество удаляемых элементов
const numberOfItemsToRemove = this.find(item, comparator).length
for (let i = 0; i < numberOfItemsToRemove; i += 1) {
// Определять индекс удаляемого элемента необходимо на каждой итерации,
// поскольку куча каждый раз модифицируется
const index = this.find(item, comparator).pop()
// Последний элемент просто удаляется
if (index === this.heapContainer.length - 1) {
this.heapContainer.pop()
} else {
// Иначе, перемещаем последний элемент на освободившееся место
this.heapContainer[index] = this.heapContainer.pop()
// Получаем родительский элемент
const parentItem = this.parent(index)
// Если предок отсутствует или неправильно расположен,
// просеиваем кучу вниз
if (
this.hasLeftChild(index) &&
(!parentItem ||
this.pairIsInCorrectOrder(parentItem, this.heapContainer[index]))
) {
this.heapifyDown(index)
} else {
// Иначе, просеиваем кучу вверх
this.heapifyUp(index)
}
}
}
return this
}
Метод поиска индексов элементов:
// Находит индексы всех элементов, равных `item`.
// Принимает искомый элемент и кастомную функцию сравнения элементов
find(item, comparator = this.compare) {
const indices = []
for (let i = 0; i < this.heapContainer.length; i += 1) {
if (comparator.equal(this.heapContainer[i], item)) {
indices.push(i)
}
}
return indices
}
Метод перестановки элементов:
// Меняет элементы местами
swap(indexOne, indexTwo) {
const tmp = this.heapContainer[indexOne]
this.heapContainer[indexOne] = this.heapContainer[indexTwo]
this.heapContainer[indexTwo] = tmp
}
Пришло время главных (и самых сложных для понимания) функций кучи.
Функция просеивания кучи вверх:
// Просеивает кучу вверх.
// Принимает кастомный индекс начальной позиции
heapifyUp(customStartIndex) {
// Берем последний элемент (последний в массиве или нижний левый в дереве)
// и поднимаем его наверх до тех пор, пока он не будет
// правильно расположен по отношению к предку
let currentIndex = customStartIndex || this.heapContainer.length - 1
while (
this.hasParent(currentIndex) &&
!this.pairIsInCorrectOrder(
this.parent(currentIndex),
this.heapContainer[currentIndex],
)
) {
this.swap(currentIndex, this.getParentIndex(currentIndex))
currentIndex = this.getParentIndex(currentIndex)
}
}
Функция просеивания кучи вниз:
// Просеивает кучу вниз.
// Принимает кастомный индекс начальной позиции (по умолчанию 0)
heapifyDown(customStartIndex = 0) {
// Сравниваем предка с его потомками и
// меняем местами предка с соответствующим потомком
// (наименьшим для min-кучи, наибольшим для max-кучи).
// Затем делаем тоже самое для следующего потомка
let currentIndex = customStartIndex
let nextIndex = null
// Пока есть левый потомок
while (this.hasLeftChild(currentIndex)) {
// Если есть правый потомок и
// потомки расположены в правильном порядке
if (
this.hasRightChild(currentIndex) &&
this.pairIsInCorrectOrder(
this.rightChild(currentIndex),
this.leftChild(currentIndex),
)
) {
// Следующим индексом является индекс правого потомка
nextIndex = this.getRightChildIndex(currentIndex)
} else {
// Иначе, следующим индексом является индекс левого потомка
nextIndex = this.getLeftChildIndex(currentIndex)
}
// Прерываем цикл, если элементы расположены в правильном порядке
if (
this.pairIsInCorrectOrder(
this.heapContainer[currentIndex],
this.heapContainer[nextIndex],
)
) {
break
}
// Меняем элементы местами
this.swap(currentIndex, nextIndex)
// Обновляем текущий индекс
currentIndex = nextIndex
}
}
Заглушка (или абстрактный метод, или контракт) для метода определения правильного расположения элементов:
// Проверяет, что пара элементов в куче расположена в правильном порядке.
// Для min-кучи первый элемент всегда должен быть меньше или равен второму.
// Для max-кучи первый элемент всегда должен быть больше или равен второму.
// Этот метод должен быть реализован соответствующими подклассами
// (min-кучей и max-кучей)
pairIsInCorrectOrder(firstElement, secondElement) {
throw new Error('Метод сравнения не реализован!')
}
Полный код кучи
// Импортируем конструктор функции сравнения узлов
import Comparator from '../../utils/comparator'
// Родительский класс для min- и max-куч
export default class Heap {
constructor(fn) {
// Кучи должны создаваться с помощью соответствующих подклассов
if (new.target === Heap) {
throw new TypeError('Кучу нельзя создавать напрямую!')
}
// Представление кучи в виде массива
this.heapContainer = []
// Функция сравнения элементов
this.compare = new Comparator(fn)
}
// Возвращает индекс левого потомка
getLeftChildIndex(parentIndex) {
return 2 * parentIndex + 1
}
// Возвращает индекс правого потомка
getRightChildIndex(parentIndex) {
return 2 * parentIndex + 2
}
// Возвращает индекс предка
getParentIndex(childIndex) {
return Math.floor((childIndex - 1) / 2)
}
// Проверяет наличие предка
hasParent(childIndex) {
return this.getParentIndex(childIndex) >= 0
}
// Проверяет наличие левого потомка
hasLeftChild(parentIndex) {
return this.getLeftChildIndex(parentIndex) < this.heapContainer.length
}
// Проверяет наличие правого потомка
hasRightChild(parentIndex) {
return this.getRightChildIndex(parentIndex) < this.heapContainer.length
}
// Возвращает левого потомка
leftChild(parentIndex) {
return this.heapContainer[this.getLeftChildIndex(parentIndex)]
}
// Возвращает правого потомка
rightChild(parentIndex) {
return this.heapContainer[this.getRightChildIndex(parentIndex)]
}
// Возвращает предка
parent(childIndex) {
return this.heapContainer[this.getParentIndex(childIndex)]
}
// Определяет пустоту кучи
isEmpty() {
return this.heapContainer.length === 0
}
// Возвращает строковое представление кучи
toString() {
return this.heapContainer.toString()
}
// Возвращает ссылку на корневой элемент кучи
// (наименьший для min-кучи, наибольший для max-кучи;
// элемент не удаляется)
peek() {
if (this.isEmpty()) {
return null
}
return this.heapContainer[0]
}
// Удаляет и возвращает корневой элемент кучи
poll() {
if (this.isEmpty()) {
return null
}
if (this.heapContainer.length === 1) {
return this.heapContainer.pop()
}
const item = this.heapContainer[0]
// Перемещаем последний элемент в начало
this.heapContainer[0] = this.heapContainer.pop()
// Просеиваем кучу вниз
this.heapifyDown()
// Возвращаем удаленный элемент
return item
}
// Добавляет элемент в кучу
add(item) {
// Добавляем новый элемент в конец кучи
this.heapContainer.push(item)
// Просеиваем кучу вверх
this.heapifyUp()
return this
}
// Удаляет элемент из кучи.
// Принимает элемент и кастомную функцию сравнения элементов
remove(item, comparator = this.compare) {
// Определяем количество удаляемых элементов
const numberOfItemsToRemove = this.find(item, comparator).length
for (let i = 0; i < numberOfItemsToRemove; i += 1) {
// Определять индекс удаляемого элемента необходимо на каждой итерации,
// поскольку куча каждый раз модифицируется
const index = this.find(item, comparator).pop()
// Последний элемент просто удаляется
if (index === this.heapContainer.length - 1) {
this.heapContainer.pop()
} else {
// Иначе, перемещаем последний элемент на освободившееся место
this.heapContainer[index] = this.heapContainer.pop()
// Получаем родительский элемент
const parentItem = this.parent(index)
// Если предок отсутствует или неправильно расположен,
// просеиваем кучу вниз
if (
this.hasLeftChild(index) &&
(!parentItem ||
this.pairIsInCorrectOrder(parentItem, this.heapContainer[index]))
) {
this.heapifyDown(index)
} else {
// Иначе, просеиваем кучу вверх
this.heapifyUp(index)
}
}
}
return this
}
// Находит индексы всех элементов, равных `item`.
// Принимает искомый элемент и кастомную функцию сравнения элементов
find(item, comparator = this.compare) {
const indices = []
for (let i = 0; i < this.heapContainer.length; i += 1) {
if (comparator.equal(this.heapContainer[i], item)) {
indices.push(i)
}
}
return indices
}
// Меняет элементы местами
swap(indexOne, indexTwo) {
const tmp = this.heapContainer[indexOne]
this.heapContainer[indexOne] = this.heapContainer[indexTwo]
this.heapContainer[indexTwo] = tmp
}
// Просеивает кучу вверх.
// Принимает кастомный индекс начальной позиции
heapifyUp(customStartIndex) {
// Берем последний элемент (последний в массиве или нижний левый в дереве)
// и поднимаем его наверх до тех пор, пока он не будет
// правильно расположен по отношению к предку
let currentIndex = customStartIndex || this.heapContainer.length - 1
while (
this.hasParent(currentIndex) &&
!this.pairIsInCorrectOrder(
this.parent(currentIndex),
this.heapContainer[currentIndex],
)
) {
this.swap(currentIndex, this.getParentIndex(currentIndex))
currentIndex = this.getParentIndex(currentIndex)
}
}
// Просеивает кучу вниз.
// Принимает кастомный индекс начальной позиции (по умолчанию 0)
heapifyDown(customStartIndex = 0) {
// Сравниваем предка с его потомками и
// меняем местами предка с соответствующим потомком
// (наименьшим для min-кучи и наибольшим для max-кучи).
// Затем делаем тоже самое для следующего потомка
let currentIndex = customStartIndex
let nextIndex = null
// Пока есть левый потомок
while (this.hasLeftChild(currentIndex)) {
// Если есть правый потомок и
// потомки расположены в правильном порядке
if (
this.hasRightChild(currentIndex) &&
this.pairIsInCorrectOrder(
this.rightChild(currentIndex),
this.leftChild(currentIndex),
)
) {
// Следующим индексом является индекс правого потомка
nextIndex = this.getRightChildIndex(currentIndex)
} else {
// Иначе, следующим индексом является индекс л�евого потомка
nextIndex = this.getLeftChildIndex(currentIndex)
}
// Прерываем цикл, если элементы расположены в правильном порядке
if (
this.pairIsInCorrectOrder(
this.heapContainer[currentIndex],
this.heapContainer[nextIndex],
)
) {
break
}
// Меняем элементы местами
this.swap(currentIndex, nextIndex)
// Обновляем текущий индекс
currentIndex = nextIndex
}
}
// Проверяет, что пара элементов в куче расположена в правильном порядке.
// Для min-кучи первый элемент всегда должен быть меньше или равен второму.
// Для max-кучи первый элемент всегда должен быть больше или равен второму.
// Этот метод должен быть реализован соответствующими подклассами
// (min-кучей и max-кучей)
pairIsInCorrectOrder(firstElement, secondElement) {
throw new Error('Метод сравнения не реализован!')
}
}
Таким образом, реализация подклассов сводится к реализации метода pairIsInCorrectOrder.
Реализация подкласса min-кучи:
// data-structures/heap/min-heap.js
import Heap from '.'
export default class MinHeap extends Heap {
pairIsInCorrectOrder(firstElement, secondElement) {
// Первый элемент должен быть меньше или равен второму
return this.compare.lessThanOrEqual(firstElement, secondElement)
}
}
Реализация подкласса max-кучи:
// data-structures/heap/max-heap.js
import Heap from '.'
export default class MaxHeap extends Heap {
pairIsInCorrectOrder(firstElement, secondElement) {
// Первый элемент должен быть больше или равен второму
return this.compare.greaterThanOrEqual(firstElement, secondElement)
}
}
Тестирование
Проверим, что наша куча работает, как ожидается.
Начнем с суперкласса:
// data-structures/heap/__tests__/heap.test.js
import Heap from '..'
describe('Heap', () => {
it('должен выбросить исключение при попытке создания кучи напрямую', () => {
const instantiateHeap = () => {
const heap = new Heap()
heap.add(5)
}
expect(instantiateHeap).toThrow()
})
})
Тестирование min-кучи
// data-structures/heap/__tests__/min-heap.test.js
import MinHeap from '../min-heap'
import Comparator from '../../../utils/comparator'
describe('MinHeap', () => {
it('должен создать пустую min-кучу', () => {
const minHeap = new MinHeap()
expect(minHeap).toBeDefined()
expect(minHeap.peek()).toBeNull()
expect(minHeap.isEmpty()).toBe(true)
})
it('должен добавить элементы в кучу и просеять ее вверх', () => {
const minHeap = new MinHeap()
minHeap.add(5)
expect(minHeap.isEmpty()).toBe(false)
expect(minHeap.peek()).toBe(5)
expect(minHeap.toString()).toBe('5')
minHeap.add(3)
expect(minHeap.peek()).toBe(3)
expect(minHeap.toString()).toBe('3,5')
minHeap.add(10)
expect(minHeap.peek()).toBe(3)
expect(minHeap.toString()).toBe('3,5,10')
minHeap.add(1)
expect(minHeap.peek()).toBe(1)
expect(minHeap.toString()).toBe('1,3,10,5')
minHeap.add(1)
expect(minHeap.peek()).toBe(1)
expect(minHeap.toString()).toBe('1,1,10,5,3')
expect(minHeap.poll()).toBe(1)
expect(minHeap.toString()).toBe('1,3,10,5')
expect(minHeap.poll()).toBe(1)
expect(minHeap.toString()).toBe('3,5,10')
expect(minHeap.poll()).toBe(3)
expect(minHeap.toString()).toBe('5,10')
})
it('должен извлечь элементы из кучи и просеять ее вниз', () => {
const minHeap = new MinHeap()
minHeap.add(5)
minHeap.add(3)
minHeap.add(10)
minHeap.add(11)
minHeap.add(1)
expect(minHeap.toString()).toBe('1,3,10,11,5')
expect(minHeap.poll()).toBe(1)
expect(minHeap.toString()).toBe('3,5,10,11')
expect(minHeap.poll()).toBe(3)
expect(minHeap.toString()).toBe('5,11,10')
expect(minHeap.poll()).toBe(5)
expect(minHeap.toString()).toBe('10,11')
expect(minHeap.poll()).toBe(10)
expect(minHeap.toString()).toBe('11')
expect(minHeap.poll()).toBe(11)
expect(minHeap.toString()).toBe('')
expect(minHeap.poll()).toBeNull()
expect(minHeap.toString()).toBe('')
})
it('должен просеять кучу вниз по правильной ветке', () => {
const minHeap = new MinHeap()
minHeap.add(3)
minHeap.add(12)
minHeap.add(10)
expect(minHeap.toString()).toBe('3,12,10')
minHeap.add(11)
expect(minHeap.toString()).toBe('3,11,10,12')
expect(minHeap.poll()).toBe(3)
expect(minHeap.toString()).toBe('10,11,12')
})
it('должен находить индексы элементов', () => {
const minHeap = new MinHeap()
minHeap.add(3)
minHeap.add(12)
minHeap.add(10)
minHeap.add(11)
minHeap.add(11)
expect(minHeap.toString()).toBe('3,11,10,12,11')
expect(minHeap.find(5)).toEqual([])
expect(minHeap.find(3)).toEqual([0])
expect(minHeap.find(11)).toEqual([1, 4])
})
it('должен удалять элементы из кучи с ее просеиванием вниз', () => {
const minHeap = new MinHeap()
minHeap.add(3)
minHeap.add(12)
minHeap.add(10)
minHeap.add(11)
minHeap.add(11)
expect(minHeap.toString()).toBe('3,11,10,12,11')
expect(minHeap.remove(3).toString()).toEqual('10,11,11,12')
expect(minHeap.remove(3).peek()).toEqual(10)
expect(minHeap.remove(11).toString()).toEqual('10,12')
expect(minHeap.remove(3).peek()).toEqual(10)
})
it('должен удалять элементы из кучи с ее просеиванием вверх', () => {
const minHeap = new MinHeap()
minHeap.add(3)
minHeap.add(10)
minHeap.add(5)
minHeap.add(6)
minHeap.add(7)
minHeap.add(4)
minHeap.add(6)
minHeap.add(8)
minHeap.add(2)
minHeap.add(1)
expect(minHeap.toString()).toBe('1,2,4,6,3,5,6,10,8,7')
expect(minHeap.remove(8).toString()).toEqual('1,2,4,6,3,5,6,10,7')
expect(minHeap.remove(7).toString()).toEqual('1,2,4,6,3,5,6,10')
expect(minHeap.remove(1).toString()).toEqual('2,3,4,6,10,5,6')
expect(minHeap.remove(2).toString()).toEqual('3,6,4,6,10,5')
expect(minHeap.remove(6).toString()).toEqual('3,5,4,10')
expect(minHeap.remove(10).toString()).toEqual('3,5,4')
expect(minHeap.remove(5).toString()).toEqual('3,4')
expect(minHeap.remove(3).toString()).toEqual('4')
expect(minHeap.remove(4).toString()).toEqual('')
})
it('должен удалить элементы из кучи, найденные с помощью кастомной функции сравнения', () => {
const minHeap = new MinHeap()
minHeap.add('dddd')
minHeap.add('ccc')
minHeap.add('bb')
minHeap.add('a')
expect(minHeap.toString()).toBe('a,bb,ccc,dddd')
const comparator = new Comparator((a, b) => {
if (a.length === b.length) {
return 0
}
return a.length < b.length ? -1 : 1
})
minHeap.remove('hey', comparator)
expect(minHeap.toString()).toBe('a,bb,dddd')
})
it('должен удалить элементы из кучи с правильной реструктуризацией дерева', () => {
const minHeap = new MinHeap()
minHeap.add(1)
minHeap.add(2)
minHeap.add(3)
minHeap.add(4)
minHeap.add(5)
minHeap.add(6)
minHeap.add(7)
minHeap.add(8)
minHeap.add(9)
expect(minHeap.toString()).toBe('1,2,3,4,5,6,7,8,9')
minHeap.remove(2)
expect(minHeap.toString()).toBe('1,4,3,8,5,6,7,9')
minHeap.remove(4)
expect(minHeap.toString()).toBe('1,5,3,8,9,6,7')
})
})
Тестирование max-кучи
// data-structures/heap/__tests__/max-heap.test.js
import MaxHeap from '../max-heap'
import Comparator from '../../../utils/comparator'
describe('MaxHeap', () => {
it('должен создать пустую max-кучу', () => {
const maxHeap = new MaxHeap()
expect(maxHeap).toBeDefined()
expect(maxHeap.peek()).toBeNull()
expect(maxHeap.isEmpty()).toBe(true)
})
it('должен добавить элементы в кучу и просеять ее вверх', () => {
const maxHeap = new MaxHeap()
maxHeap.add(5)
expect(maxHeap.isEmpty()).toBe(false)
expect(maxHeap.peek()).toBe(5)
expect(maxHeap.toString()).toBe('5')
maxHeap.add(3)
expect(maxHeap.peek()).toBe(5)
expect(maxHeap.toString()).toBe('5,3')
maxHeap.add(10)
expect(maxHeap.peek()).toBe(10)
expect(maxHeap.toString()).toBe('10,3,5')
maxHeap.add(1)
expect(maxHeap.peek()).toBe(10)
expect(maxHeap.toString()).toBe('10,3,5,1')
maxHeap.add(1)
expect(maxHeap.peek()).toBe(10)
expect(maxHeap.toString()).toBe('10,3,5,1,1')
expect(maxHeap.poll()).toBe(10)
expect(maxHeap.toString()).toBe('5,3,1,1')
expect(maxHeap.poll()).toBe(5)
expect(maxHeap.toString()).toBe('3,1,1')
expect(maxHeap.poll()).toBe(3)
expect(maxHeap.toString()).toBe('1,1')
})
it('должен извлечь элементы из кучи и просеять ее вниз', () => {
const maxHeap = new MaxHeap()
maxHeap.add(5)
maxHeap.add(3)
maxHeap.add(10)
maxHeap.add(11)
maxHeap.add(1)
expect(maxHeap.toString()).toBe('11,10,5,3,1')
expect(maxHeap.poll()).toBe(11)
expect(maxHeap.toString()).toBe('10,3,5,1')
expect(maxHeap.poll()).toBe(10)
expect(maxHeap.toString()).toBe('5,3,1')
expect(maxHeap.poll()).toBe(5)
expect(maxHeap.toString()).toBe('3,1')
expect(maxHeap.poll()).toBe(3)
expect(maxHeap.toString()).toBe('1')
expect(maxHeap.poll()).toBe(1)
expect(maxHeap.toString()).toBe('')
expect(maxHeap.poll()).toBeNull()
expect(maxHeap.toString()).toBe('')
})
it('должен просеять кучу вниз по правильной ветке', () => {
const maxHeap = new MaxHeap()
maxHeap.add(3)
maxHeap.add(12)
maxHeap.add(10)
expect(maxHeap.toString()).toBe('12,3,10')
maxHeap.add(11)
expect(maxHeap.toString()).toBe('12,11,10,3')
expect(maxHeap.poll()).toBe(12)
expect(maxHeap.toString()).toBe('11,3,10')
})
it('должен находить индексы элементов', () => {
const maxHeap = new MaxHeap()
maxHeap.add(3)
maxHeap.add(12)
maxHeap.add(10)
maxHeap.add(11)
maxHeap.add(11)
expect(maxHeap.toString()).toBe('12,11,10,3,11')
expect(maxHeap.find(5)).toEqual([])
expect(maxHeap.find(12)).toEqual([0])
expect(maxHeap.find(11)).toEqual([1, 4])
})
it('должен удалять элементы из кучи с ее просеиванием вниз', () => {
const maxHeap = new MaxHeap()
maxHeap.add(3)
maxHeap.add(12)
maxHeap.add(10)
maxHeap.add(11)
maxHeap.add(11)
expect(maxHeap.toString()).toBe('12,11,10,3,11')
expect(maxHeap.remove(12).toString()).toEqual('11,11,10,3')
expect(maxHeap.remove(12).peek()).toEqual(11)
expect(maxHeap.remove(11).toString()).toEqual('10,3')
expect(maxHeap.remove(10).peek()).toEqual(3)
})
it('должен удалять элементы из кучи с ее просеиванием вверх', () => {
const maxHeap = new MaxHeap()
maxHeap.add(3)
maxHeap.add(10)
maxHeap.add(5)
maxHeap.add(6)
maxHeap.add(7)
maxHeap.add(4)
maxHeap.add(6)
maxHeap.add(8)
maxHeap.add(2)
maxHeap.add(1)
expect(maxHeap.toString()).toBe('10,8,6,7,6,4,5,3,2,1')
expect(maxHeap.remove(4).toString()).toEqual('10,8,6,7,6,1,5,3,2')
expect(maxHeap.remove(3).toString()).toEqual('10,8,6,7,6,1,5,2')
expect(maxHeap.remove(5).toString()).toEqual('10,8,6,7,6,1,2')
expect(maxHeap.remove(10).toString()).toEqual('8,7,6,2,6,1')
expect(maxHeap.remove(6).toString()).toEqual('8,7,1,2')
expect(maxHeap.remove(2).toString()).toEqual('8,7,1')
expect(maxHeap.remove(1).toString()).toEqual('8,7')
expect(maxHeap.remove(7).toString()).toEqual('8')
expect(maxHeap.remove(8).toString()).toEqual('')
})
it('должен удалить элементы из кучи, найденные с помощью кастомной функции сравнения', () => {
const maxHeap = new MaxHeap()
maxHeap.add('a')
maxHeap.add('bb')
maxHeap.add('ccc')
maxHeap.add('dddd')
expect(maxHeap.toString()).toBe('dddd,ccc,bb,a')
const comparator = new Comparator((a, b) => {
if (a.length === b.length) {
return 0
}
return a.length < b.length ? -1 : 1
})
maxHeap.remove('hey', comparator)
expect(maxHeap.toString()).toBe('dddd,a,bb')
})
})
Запускаем тесты:
npm run test ./data-structures/heap
Результат:

Очередь с приоритетом
Описание
Очередь с приоритетом (priority queue) - это абстрактный тип данных, похожий на обычную очередь (см. часть 1, раздел 3) или стек (см. часть 1, раздел 4), за исключением того, что в ней каждый элемент имеет определенный "приоритет" (priority). Элемент с более высоким приоритетом обрабатывается перед элементом с более низким приоритетом. Если два элемента имеют одинаковый приоритет, они обрабатываются в порядке их расположения в очереди.
Несмотря на то, что очереди с приоритетом часто реализуются с помощью куч, они концептуально различаются. Очередь с приоритетом - это абстрактная концепция, вроде "списка" (list) или "карты" (map). Как список может быть реализован с помощью связного списка (см. часть 1, раздел 1) или массива, так и очередь с приоритетом может быть реализована с помощью кучи или другим способом, например, с помощью неупорядоченного массива.
Интерактивную визуализации очереди с приоритетом можно посмотреть здесь.
Сложность
Временная сложность очереди с приоритетом составляет O(n) или O(n*log(n)) (зависит от реализации).
Реализация
Для реализации очереди с приоритетом мы воспользуемся min-кучей (см. предыдущий раздел).
Начнем с конструктора:
// data-structures/priority-queue.js
// Импортируем конструктор функции сравнения узлов
import Comparator from '../utils/comparator'
// Импортируем конструктор min-кучи
import MinHeap from './heap/min-heap'
// Очередь с приоритетом.
// Реализация на основе min-кучи
export default class PriorityQueue extends MinHeap {
constructor() {
// Инициализируем min-кучу
super()
// Карта приоритетов
this.priorities = new Map()
// Функция сравнения элементов
this.compare = new Comparator(this.comparePriorities.bind(this))
}
}
Методы добавления и удаления элементов в/из очереди:
// Добавляет элемент в очередь.
// Принимает элемент и приоритет.
// Чем больше приоритет (меньше значение `priority`),
// тем "выше" элемент находится в очереди
add(item, priority = 0) {
// Обновляем приоритеты
this.priorities.set(item, priority)
// Добавляем элемент в кучу
super.add(item)
return this
}
// Удаляет элемент из очереди.
// Принимает элемент и кастомную функцию сравнения элементов
remove(item, compare) {
// Удаляем элемент из кучи
super.remove(item, compare)
// Обновляем приоритеты
this.priorities.delete(item)
return this
}
Метод обновления приоритета:
// Обновляет приоритет.
// Принимает элемент и новый приоритет
changePriority(item, priority) {
// Удаляем элемент из очереди
this.remove(item, new Comparator(this.compareValues))
// Добавляем элемент с новым приоритетом
this.add(item, priority)
return this
}
Метод поиска элемента по значению и определения наличия элемента:
// Ищет элемент по значению.
// Возвращает массив индексов
findByValue(item) {
return this.find(item, new Comparator(this.compareValues))
}
// Определяет наличие элемента
hasValue(item) {
return this.findByValue(item).length > 0
}
Методы сравнения элементов по приоритетам и значениям:
// Сравнивает приоритеты
comparePriorities(a, b) {
// Вызываем функцию сравнения значений,
// передавая ей приоритеты
return this.compareValues(this.priorities.get(a), this.priorities.get(b))
}
// Сравнивает значения
compareValues(a, b) {
if (a === b) {
return 0
}
return a < b ? -1 : 1
}
Полный код очереди с приоритетом
// Импортируем конструктор функции сравнения узлов
import Comparator from '../utils/comparator'
// Импортируем конструктор min-кучи
import MinHeap from './heap/min-heap'
// Очередь с приоритетом.
// Реализация на основе min-кучи
export default class PriorityQueue extends MinHeap {
constructor() {
// Инициализируем min-кучу
super()
// Карта приоритетов
this.priorities = new Map()
// Функция сравнения элементов
this.compare = new Comparator(this.comparePriorities.bind(this))
}
// Добавляет элемент в очередь.
// Принимает элемент и приоритет.
// Чем больше приоритет (меньше значение `priority`),
// тем "выше" элемент находится в очереди
add(item, priority = 0) {
// Обновляем приоритеты
this.priorities.set(item, priority)
// Добавляем элемент в кучу
super.add(item)
return this
}
// Удаляет элемент из очереди.
// Принимает элемент и кастомную функцию сравнения элементов
remove(item, compare) {
// Удаляем элемент из кучи
super.remove(item, compare)
// Обновляем пр�иоритеты
this.priorities.delete(item)
return this
}
// Обновляет приоритет.
// Принимает элемент и новый приоритет
changePriority(item, priority) {
// Удаляем элемент из очереди
this.remove(item, new Comparator(this.compareValues))
// Добавляем элемент с новым приоритетом
this.add(item, priority)
return this
}
// Ищет элемент по значению.
// Возвращает массив индексов
findByValue(item) {
return this.find(item, new Comparator(this.compareValues))
}
// Определяет наличие элемента
hasValue(item) {
return this.findByValue(item).length > 0
}
// Сравнивает приоритеты
comparePriorities(a, b) {
// Вызываем функцию сравнения значений,
// передавая ей приоритеты
return this.compareValues(this.priorities.get(a), this.priorities.get(b))
}
// Сравнивает значения
compareValues(a, b) {
if (a === b) {
return 0
}
return a < b ? -1 : 1
}
}
Тестирование
Проверяем, что наша очередь с приоритетом работает, как ожидается
import PriorityQueue from '../priority-queue'
describe('PriorityQueue', () => {
it('должен создать дефолтную очередь с приоритетом', () => {
const priorityQueue = new PriorityQueue()
expect(priorityQueue).toBeDefined()
})
it('должен добавить элементы с приоритетом в очередь', () => {
const priorityQueue = new PriorityQueue()
priorityQueue.add(10, 1)
expect(priorityQueue.peek()).toBe(10)
priorityQueue.add(5, 2)
expect(priorityQueue.peek()).toBe(10)
priorityQueue.add(100, 0)
expect(priorityQueue.peek()).toBe(100)
})
it('должен добавить в очередь объекты', () => {
const priorityQueue = new PriorityQueue()
const user1 = { name: 'Mike' }
const user2 = { name: 'Bill' }
const user3 = { name: 'Jane' }
priorityQueue.add(user1, 1)
expect(priorityQueue.peek()).toBe(user1)
priorityQueue.add(user2, 2)
expect(priorityQueue.peek()).toBe(user1)
priorityQueue.add(user3, 0)
expect(priorityQueue.peek()).toBe(user3)
})
it('должен извлечь элементы из очереди со�гласно приоритету', () => {
const priorityQueue = new PriorityQueue()
priorityQueue.add(10, 1)
priorityQueue.add(5, 2)
priorityQueue.add(100, 0)
priorityQueue.add(200, 0)
expect(priorityQueue.poll()).toBe(100)
expect(priorityQueue.poll()).toBe(200)
expect(priorityQueue.poll()).toBe(10)
expect(priorityQueue.poll()).toBe(5)
})
it('должен обновить приоритеты головных узлов', () => {
const priorityQueue = new PriorityQueue()
priorityQueue.add(10, 1)
priorityQueue.add(5, 2)
priorityQueue.add(100, 0)
priorityQueue.add(200, 0)
expect(priorityQueue.peek()).toBe(100)
priorityQueue.changePriority(100, 10)
priorityQueue.changePriority(10, 20)
expect(priorityQueue.poll()).toBe(200)
expect(priorityQueue.poll()).toBe(5)
expect(priorityQueue.poll()).toBe(100)
expect(priorityQueue.poll()).toBe(10)
})
it('должен обновить приоритеты внутренних узлов', () => {
const priorityQueue = new PriorityQueue()
priorityQueue.add(10, 1)
priorityQueue.add(5, 2)
priorityQueue.add(100, 0)
priorityQueue.add(200, 0)
expect(priorityQueue.peek()).toBe(100)
priorityQueue.changePriority(200, 10)
priorityQueue.changePriority(10, 20)
expect(priorityQueue.poll()).toBe(100)
expect(priorityQueue.poll()).toBe(5)
expect(priorityQueue.poll()).toBe(200)
expect(priorityQueue.poll()).toBe(10)
})
it('должен обновить приоритеты и добавить элемент', () => {
const priorityQueue = new PriorityQueue()
priorityQueue.add(10, 1)
priorityQueue.add(5, 2)
priorityQueue.add(100, 0)
priorityQueue.add(200, 0)
priorityQueue.changePriority(200, 10)
priorityQueue.changePriority(10, 20)
priorityQueue.add(15, 15)
expect(priorityQueue.poll()).toBe(100)
expect(priorityQueue.poll()).toBe(5)
expect(priorityQueue.poll()).toBe(200)
expect(priorityQueue.poll()).toBe(15)
expect(priorityQueue.poll()).toBe(10)
})
it('должен определить наличие значений элементов', () => {
const priorityQueue = new PriorityQueue()
priorityQueue.add(10, 1)
priorityQueue.add(5, 2)
priorityQueue.add(100, 0)
priorityQueue.add(200, 0)
priorityQueue.add(15, 15)
expect(priorityQueue.hasValue(70)).toBe(false)
expect(priorityQueue.hasValue(15)).toBe(true)
})
})
Запускаем тесты:
npm run test ./data-structures/__tests__/priority-queue
Результат:

Префиксное дерево
Префиксное дерево (или бор, или луч, или нагруженное дерево) (trie) - структура данных, позволяющая хранить ассоциативный массив (или другое динамическое множество), ключами которого чаще всего являются строки. Представляет собой корневое дерево, каждое ребро которого помечено каким-то символом так, что для любого узла все ребра, соединяющие этот узел с его потомками, помечены разными символами. Некоторые узлы префиксного дерева выделены и считается, что префиксное дерево содержит данную строку-ключ тогда и только тогда, когда эту строку можно прочитать на пути из корня до некоторого (единственного для этой строки) выделенного узла.
Таким образом, в отличие от бинарных деревьев поиска (binary search tree), ключ, идентифицирующий конкретный узел дерева, не явно хранится в данном узле, а задается положением данного узла в дереве. Получить ключ можно выписыванием символов, помечающих ребра на пути от корня до узла. Ключ корневого узла - пустая строка. Часто в выделенных узлах хранят дополнительную информацию, связанную с ключом, и обычно выделенными являются только листья, а иногда и некоторые внутренние узлы.

Сложность
Временная сложность префиксного дерева составляет O(n) (при использовании хэш-таблицы).
Реализация
Для реализации префиксного дерева мы б�удем использовать хэш-таблицу (см. раздел 5).
Начнем с узла дерева:
// data-structures/trie/node.js
// Импортируем конструктор хэш-таблицы
import HashTable from '../hash-table'
// Последний (завершающий) символ
export const HEAD_CHARACTER = '*'
// Узел префиксного дерева
export default class Node {
constructor(char, isCompleteWord = false) {
// Символ
this.char = char
// Индикатор завершающего символа
this.isCompleteWord = isCompleteWord
// Хэш-таблица потомков
this.children = new HashTable()
}
}
Методы добавления и удаления узлов-потомков:
// Добавляет потомка в дерево
addChild(char, isCompleteWord = false) {
// Добавляем узел при отсутствии
if (!this.hasChild(char)) {
this.children.set(char, new Node(char, isCompleteWord))
}
// Извлекаем узел
const node = this.getChild(char)
// Обновляем флаг `isCompleteWord` при необходимости,
// например, при добавлении слова "car" после слова "carpet",
// букву "r" нужно пометить как завершающую
node.isCompleteWord = node.isCompleteWord || isCompleteWord
// Возвращаем узел
return node
}
// Удаляет потомка
removeChild(char) {
// Извлекаем узел
const node = this.getChild(char)
// Удаляем узел, только если:
// - у него нет потомков
// - node.isCompleteWord === false
if (node && !node.isCompleteWord && !node.hasChildren()) {
this.children.remove(char)
}
return this
}
Вспомогательные методы для работы с потомками:
// Возвращает потомка
getChild(char) {
return this.children.get(char)
}
// Определяет наличие потомка
hasChild(char) {
return this.children.has(char)
}
// Определяет наличие потомков
hasChildren() {
return this.children.getKeys().length > 0
}
// Автодополнение (предложение следующих символов)
suggestChildren() {
return [...this.children.getKeys()]
}
Метод преобразования потомков в строку:
// Преобразует потомков в строку
// с указанием признака завершающего символа
toString() {
let childrenAsString = this.suggestChildren().toString()
childrenAsString = childrenAsString ? `:${childrenAsString}` : ''
const isCompleteString = this.isCompleteWord ? HEAD_CHARACTER : ''
return `${this.char}${isCompleteString}${childrenAsString}`
}
Полный код узла префиксного дерева
// Импортируем конструктор хэш-таблицы
import HashTable from '../hash-table'
// Последний (завершающий) символ
export const HEAD_CHARACTER = '*'
// Узел префиксного дерева
export default class Node {
constructor(char, isCompleteWord = false) {
// Символ
this.char = char
// Индикатор завершающего символа
this.isCompleteWord = isCompleteWord
// Хэш-таблица потомков
this.children = new HashTable()
}
// Добавляет потомка в дерево
addChild(char, isCompleteWord = false) {
// Добавляем узел при отсутствии
if (!this.hasChild(char)) {
this.children.set(char, new Node(char, isCompleteWord))
}
// Извлекаем узел
const node = this.getChild(char)
// Обновляем флаг `isCompleteWord` при необходимости,
// например, при добавлении слова "car" после слова "carpet",
// букву "r" нужно пометить как завершающую
node.isCompleteWord = node.isCompleteWord || isCompleteWord
// Возвращаем узел
return node
}
// Удаляет потомка
removeChild(char) {
// Извлекаем узел
const node = this.getChild(char)
// Удаляем узел, только если:
// - у него нет потомков
// - node.isCompleteWord === false
if (node && !node.isCompleteWord && !node.hasChildren()) {
this.children.remove(char)
}
return this
}
// Возвращает потомка
getChild(char) {
return this.children.get(char)
}
// Определяет наличие потомка
hasChild(char) {
return this.children.has(char)
}
// Определяет наличие потомков
hasChildren() {
return this.children.getKeys().length > 0
}
// Автодополнение (предложение следующих символов)
suggestChildren() {
return [...this.children.getKeys()]
}
// Преобразует потомков в строку
// с указанием признака завершающего символа
toString() {
let childrenAsString = this.suggestChildren().toString()
childrenAsString = childrenAsString ? `:${childrenAsString}` : ''
const isCompleteString = this.isCompleteWord ? HEAD_CHARACTER : ''
return `${this.char}${isCompleteString}${childrenAsString}`
}
}
Отлично! Приступаем к реализации самого дерева:
// data-structures/trie/index.js
import TrieNode, { HEAD_CHARACTER } from './node'
// Префиксное дерево
export default class Trie {
constructor() {
// Головной (корневой) узел
this.head = new TrieNode(HEAD_CHARACTER)
}
}
Методы добавления и удаления слова (ключа) в/из дерева:
// Добавляет слово (ключ) в дерево
addWord(word) {
// Преобразуем строку (слово) в массив символов
// (вопрос на засыпку: почему лучше не использовать `split('')`?
// Подсказка: попробуйте преобразовать "Hello, 👋!")
const chars = [...word]
// Текущий узел (начинаем с головного)
let node = this.head
// Перебираем символы и добавляем каждый в дерево
for (let i = 0; i < chars.length; i++) {
// Индикатор завершающего символа
const isComplete = i === chars.length - 1
// Добавляем потомка
node = node.addChild(chars[i], isComplete)
}
return this
}
// Удаляет слово (ключ) из дерева
removeWord(word) {
// Удаляет слово рекурсивно ("сначала в глубину")
const depthFirstRemove = (node, i = 0) => {
// Если удаляемый символ находится за пределами слова,
// ничего не делаем
if (i >= word.length) return
// Символ
const char = word[i]
// Следующий узел
const nextNode = node.getChild(char)
// Если следующий узел отсутствует,
// ничего не делаем
if (!nextNode) return
// Погружаемся глубже
depthFirstRemove(nextNode, i + 1)
// Поскольку мы удаляем слово,
// необходимо обновить флаг `isCompleteWord`
// его последнего символа
if (i === word.length - 1) {
nextNode.isCompleteWord = false
}
// Узел удаляется, только если:
// - у него нет потомков
// - nextNode.isCompleteWord === false
node.removeChild(char)
}
// Начинаем с головного узла
depthFirstRemove(this.head)
return this
}
Метод автодополнения:
// Автодополнение (предложение следующих символов)
suggestNextCharacters(word) {
// Получаем последний символ
const lastChar = this.getLastCharNode(word)
// Если последний символ отсутствует
if (!lastChar) {
return null
}
// Возвра�щаем массив следующих символов
return lastChar.suggestChildren()
}
Вспомогательный метод определения наличия слова в дереве:
// Определяет наличие слова в дереве
doesWordExist(word) {
// Получаем последний символ
const lastChar = this.getLastCharNode(word)
return Boolean(lastChar) && lastChar.isCompleteWord
}
Наконец, метод получения последнего символа:
// Возвращает последний символ
getLastCharNode(word) {
// Разбиваем слово на символы
const chars = [...word]
// Текущий узел (начинаем с головного)
let node = this.head
// Перебираем символы
for (let i = 0; i < chars.length; i++) {
// Если символ отсутствует
if (!node.hasChild(chars[i])) {
return null
}
// Извлекаем потомка
node = node.getChild(chars[i])
}
// Возвращаем последний узел
return node
}
Полный код префиксного дерева
import TrieNode, { HEAD_CHARACTER } from './node'
// Префиксное дерево
export default class Trie {
constructor() {
// Головной (корневой) узел
this.head = new TrieNode(HEAD_CHARACTER)
}
// Добавляет слово (ключ) в дерево
addWord(word) {
// Преобразуем строку (слово) в массив символов
// (вопрос на засыпку: почему лучше не использовать `split()`?
// Подсказка: попробуйте преобразовать "Hello, 👋!")
const chars = [...word]
// Текущий узел (начинаем с головного)
let node = this.head
// Перебираем символы и добавляем каждый в дерево
for (let i = 0; i < chars.length; i++) {
// Индикатор последнего (завершающего) символа
const isComplete = i === chars.length - 1
// Добавляем потомка
node = node.addChild(chars[i], isComplete)
}
return this
}
// Удаляет слово (ключ) из дерева
removeWord(word) {
// Удаляет слово рекурсивно ("сначала в глубину")
const depthFirstRemove = (node, i = 0) => {
// Если удаляемый символ находится за пределами слова,
// ничего не делаем
if (i >= word.length) return
// Символ
const char = word[i]
// Следующий узел
const nextNode = node.getChild(char)
// Если следующий узел отсутствует,
// ничего не делаем
if (!nextNode) return
// Погружаемся глубже
depthFirstRemove(nextNode, i + 1)
// Поскольку мы удаляем слово,
// необходимо обновить флаг `isCompleteWord`
// его последнего символа
if (i === word.length - 1) {
nextNode.isCompleteWord = false
}
// Узел удаляется, только если:
// - у него нет потомков
// - nextNode.isCompleteWord === false
node.removeChild(char)
}
// Начинаем с головного узла
depthFirstRemove(this.head)
return this
}
// Автодополнение (предложение следующих символов)
suggestNextCharacters(word) {
// Получаем последний символ
const lastChar = this.getLastCharNode(word)
// Если последний символ отсутствует
if (!lastChar) {
return null
}
// Возвращаем массив следующих символов
return lastChar.suggestChildren()
}
// Определяет наличие слова в дереве
doesWordExist(word) {
// Получаем последний символ
const lastChar = this.getLastCharNode(word)
return Boolean(lastChar) && lastChar.isCompleteWord
}
// Возвращает последний символ
getLastCharNode(word) {
// Разбиваем слово на символы
const chars = [...word]
// Текущий узел (начинаем с головного)
let node = this.head
// Перебираем символы
for (let i = 0; i < chars.length; i++) {
// Если символ отсутствует
if (!node.hasChild(chars[i])) {
return null
}
// Извлекаем потомка
node = node.getChild(chars[i])
}
// Возвращаем последний узел
return node
}
}
Тестирование
Проверяем, что наше префиксное дерево работает, как ожидается.
Тестирование узла
// data-structures/trie/__tests__/node.test.js
import TrieNode from '../node'
describe('TrieNode', () => {
it('должен создать узел префиксного дерева', () => {
const trieNode = new TrieNode('c', true)
expect(trieNode.char).toBe('c')
expect(trieNode.isCompleteWord).toBe(true)
expect(trieNode.toString()).toBe('c*')
})
it('должен добавить потомков', () => {
const trieNode = new TrieNode('c')
trieNode.addChild('a', true)
trieNode.addChild('o')
expect(trieNode.toString()).toBe('c:a,o')
})
it('должен извлечь потомков', () => {
const trieNode = new TrieNode('c')
trieNode.addChild('a')
trieNode.addChild('o')
expect(trieNode.getChild('a').toString()).toBe('a')
expect(trieNode.getChild('a').char).toBe('a')
expect(trieNode.getChild('o').toString()).toBe('o')
expect(trieNode.getChild('b')).toBeNull()
})
it('должен определить наличие потомков', () => {
const trieNode = new TrieNode('c')
expect(trieNode.hasChildren()).toBe(false)
trieNode.addChild('a')
expect(trieNode.hasChildren()).toBe(true)
})
it('должен определить наличие конкретного потомка', () => {
const trieNode = new TrieNode('c')
trieNode.addChild('a')
trieNode.addChild('o')
expect(trieNode.hasChild('a')).toBe(true)
expect(trieNode.hasChild('o')).toBe(true)
expect(trieNode.hasChild('b')).toBe(false)
})
it('должен получить следующие символы', () => {
const trieNode = new TrieNode('c')
trieNode.addChild('a')
trieNode.addChild('o')
expect(trieNode.suggestChildren()).toEqual(['a', 'o'])
})
it('должен удалить потомка, если у него НЕТ потомков', () => {
const trieNode = new TrieNode('c')
trieNode.addChild('a')
expect(trieNode.hasChild('a')).toBe(true)
trieNode.removeChild('a')
expect(trieNode.hasChild('a')).toBe(false)
})
it('НЕ должен удалять потомков, у которых есть потомки', () => {
const trieNode = new TrieNode('c')
trieNode.addChild('a')
const childNode = trieNode.getChild('a')
childNode.addChild('r')
trieNode.removeChild('a')
expect(trieNode.hasChild('a')).toEqual(true)
})
it('НЕ должен удалять потомков, которые являются завершающими символами', () => {
const trieNode = new TrieNode('c')
const IS_COMPLETE_WORD = true
trieNode.addChild('a', IS_COMPLETE_WORD)
trieNode.removeChild('a')
expect(trieNode.hasChild('a')).toEqual(true)
})
})
Тестирование дерева
// data-structures/trie/__tests__/trie.test.js
import Trie from '..'
describe('Trie', () => {
it('должен создать префиксное дерево', () => {
const trie = new Trie()
expect(trie).toBeDefined()
expect(trie.head.toString()).toBe('*')
})
it('должен добавить слова в дерево', () => {
const trie = new Trie()
trie.addWord('cat')
expect(trie.head.toString()).toBe('*:c')
expect(trie.head.getChild('c').toString()).toBe('c:a')
trie.addWord('car')
expect(trie.head.toString()).toBe('*:c')
expect(trie.head.getChild('c').toString()).toBe('c:a')
expect(trie.head.getChild('c').getChild('a').toString()).toBe('a:t,r')
expect(trie.head.getChild('c').getChild('a').getChild('t').toString()).toBe(
't*',
)
})
it('должен удалить слова из дерева', () => {
const trie = new Trie()
trie.addWord('carpet')
trie.addWord('car')
trie.addWord('cat')
trie.addWord('cart')
expect(trie.doesWordExist('carpet')).toBe(true)
expect(trie.doesWordExist('car')).toBe(true)
expect(trie.doesWordExist('cart')).toBe(true)
expect(trie.doesWordExist('cat')).toBe(true)
// Пытаемся удалить несуществующее слово
trie.removeWord('carpool')
expect(trie.doesWordExist('carpet')).toBe(true)
expect(trie.doesWordExist('car')).toBe(true)
expect(trie.doesWordExist('cart')).toBe(true)
expect(trie.doesWordExist('cat')).toBe(true)
trie.removeWord('carpet')
expect(trie.doesWordExist('carpet')).toEqual(false)
expect(trie.doesWordExist('car')).toEqual(true)
expect(trie.doesWordExist('cart')).toBe(true)
expect(trie.doesWordExist('cat')).toBe(true)
trie.removeWord('cat')
expect(trie.doesWordExist('car')).toEqual(true)
expect(trie.doesWordExist('cart')).toBe(true)
expect(trie.doesWordExist('cat')).toBe(false)
trie.removeWord('car')
expect(trie.doesWordExist('car')).toEqual(false)
expect(trie.doesWordExist('cart')).toBe(true)
trie.removeWord('cart')
expect(trie.doesWordExist('car')).toEqual(false)
expect(trie.doesWordExist('cart')).toBe(false)
})
it('должен получить следующие символы', () => {
const trie = new Trie()
trie.addWord('cat')
trie.addWord('cats')
trie.addWord('car')
trie.addWord('caption')
expect(trie.suggestNextCharacters('ca')).toEqual(['t', 'r', 'p'])
expect(trie.suggestNextCharacters('cat')).toEqual(['s'])
expect(trie.suggestNextCharacters('cab')).toBeNull()
})
it('должен определить наличие слов', () => {
const trie = new Trie()
trie.addWord('cat')
trie.addWord('cats')
trie.addWord('carpet')
trie.addWord('car')
trie.addWord('caption')
expect(trie.doesWordExist('cat')).toBe(true)
expect(trie.doesWordExist('cats')).toBe(true)
expect(trie.doesWordExist('carpet')).toBe(true)
expect(trie.doesWordExist('car')).toBe(true)
expect(trie.doesWordExist('cap')).toBe(false)
expect(trie.doesWordExist('call')).toBe(false)
})
})
Запускаем тесты:
npm run test ./data-structures/trie
Результат:

Дерево
Дерево (tree) - это широко распространенный абстрактный тип данных (АТД) или структура данных, реализующая этот АТД, которая симулирует иерархическую структуру дерева с корневым узлом и поддеревьями потомков с родительским узлом, представленными как связные списки.
Древовидная структура данных может быть определена рекурсивно (локально) как коллекция узлов (начиная с корневого), где каждый узел содержит значение и список ссылок на другие узлы (потомки) с тем ограничением, что ссылки не дублируются и не указывают на корень.

Пример простого неупорядоченного дерева. Узел со значением 3 имеет двух потомков со значениями 2 и 6 и одного предка со значением 2. Корневой узел на вершине предков не имеет.
Двоичное дерево поиска
Описание
Двоичное (или бинарное) дерево поиска (binary search tree, BST) (ДДП), иногда называемое упорядоченным или отсортированным двоичным деревом, - это структура данных для хранения "элементов" (чисел, имен и др.) в памяти. Она позволяет выполнять быстрый поиск, добавление и удаление элементов и может использоваться для реализации динамических множеств элементов или поисковых таблиц, позволяющих искать значения по ключу (например, искать номер телефона по имени человека).
Ключи ДДП являются отсортированными, поэтому поиск и другие операции полагаются на принцип двоичного поиска: при поиске ключа (или места для его добавления) дерево обходится от корня к листьям, ключи, хранящиеся в узлах, сравниваются, и принимается решение о том, в каком поддереве, правом или левом, продолжать поиск. В среднем, это означает, что выполнение операции обходится примерно в два раза дешевле, т.е. поиск, вставка и удаление выполняются за время, пропорциональное логарифму количества элементов, хранящихся в дереве. Это лучше, чем линейное время, необходимое для поиска элемента по ключу в (неупорядоченном) массиве, но хуже, чем соответствующие операции хзш-таблицы (см. часть 2, раздел 5).

ДДП размером 9 и глубиной (высотой) 3 с корнем со значением 8.
Интерактивную визуализации ДДП можно посмотреть здесь.
Сложность
Временная
| Поиск | Вставка | Удаление |
|---|---|---|
O(log n) | O(log n) | O(log n) |
Пространственная
O(n)
Реализация
Начнем с реализации суперкласса узла двоичного дерева:
// data-structures/tree/binary-tree-node.js
import Comparator from '../../utils/comparator'
import HashTable from '../hash-table'
export default class BinaryTreeNode {
constructor(value = null) {
// Значение
this.value = value
// Левый потомок
this.left = null
// Правый потомок
this.right = null
// Предок
this.parent = null
// Дополнительная информация об узле
this.meta = new HashTable()
// Функция сравнения узлов
this.nodeComparator = new Comparator()
}
}
Несколько геттеров для получения высоты (глубины) поддеревьев:
// Геттер высоты (глубины) левого поддерева
get leftHeight() {
if (!this.left) {
return 0
}
return this.left.height + 1
}
// Геттер высоты правого поддерева
get rightHeight() {
if (!this.right) {
return 0
}
return this.right.height + 1
}
// Геттер максимальной высоты
get height() {
return Math.max(this.leftHeight, this.rightHeight)
}
// Геттер разницы между высотой левого и правого поддеревьев
// (фактор балансировки, баланс-фактор)
get balanceFactor() {
return this.leftHeight - this.rightHeight
}
Для определения правильного места для вставки элемента нам также потребуется геттер узла, соседнего с родительским (дяди):
// Геттер дяди
get uncle() {
// Если нет предка, то нет и дяди
if (!this.parent) {
return null
}
// Если нет дедушки, то нет и дяди
if (!this.parent.parent) {
return null
}
// Если у дедушки нет двух потомков, то нет и дяди
if (!this.parent.parent.left || !this.parent.parent.right) {
return null
}
// Выясняем, кто является дядей
// путем сравнения предка с потомком дедушки
if (this.nodeComparator.equal(this.parent, this.parent.parent.left)) {
// Дядя - правый узел
return this.parent.parent.right
}
// Дядя - левый узел
return this.parent.parent.left
}
Методы установки значения, левого и правого потомков:
// Устанавливает значение
setValue(value) {
this.value = value
return this
}
// Устанавливает левого потомок
setLeft(node) {
// Сбрасываем предка левого узла
if (this.left) {
this.left.parent = null
}
// Обновляем левый узел
this.left = node
// Делаем текущий узел предком нового левого узла
if (this.left) {
this.left.parent = this
}
return this
}
// Устанавливает правого потомка
setRight(node) {
// Сбрасываем предка правого узла
if (this.right) {
this.right.parent = null
}
// Обновляем правый узел
this.right = node
// Делаем текущий узел предком нового правого узла
if (this.right) {
this.right.parent = this
}
return this
}
Методы удаления и замены потомка:
// Удаляет потомка
removeChild(nodeToRemove) {
// Если удаляется левый потомок
if (this.left && this.nodeComparator.equal(this.left, nodeToRemove)) {
this.left = null
return true
}
// Если удаляется правый потомок
if (this.right && this.nodeComparator.equal(this.right, nodeToRemove)) {
this.right = null
return true
}
return false
}
// Заменяет потомка
replaceChild(nodeToReplace, replacementNode) {
if (!nodeToReplace || !replacementNode) {
return false
}
// Если заменяется левый потомок
if (this.left && this.nodeComparator.equal(this.left, nodeToReplace)) {
this.left = replacementNode
return true
}
// Если заменяется правый потомок
if (this.right && this.nodeComparator.equal(this.right, nodeToReplace)) {
this.right = replacementNode
return true
}
return false
}
Метод обхода дерева в порядке возрастания ключей (симметричный обход):
// Обх�одит дерево в порядке возрастания ключей (inorder, infix traverse):
// сначала обходится левое поддерево, затем корень, затем правое поддерево
traverseInOrder() {
let result = []
if (this.left) {
result = result.concat(this.left.traverseInOrder())
}
result.push(this.value)
if (this.right) {
result = result.concat(this.right.traverseInOrder())
}
return result
}
Статический метод копирования узла и метод преобразования дерева в строку:
// Статический метод копирования узла
static copyNode(sourceNode, targetNode) {
targetNode.setValue(sourceNode.value)
targetNode.setLeft(sourceNode.left)
targetNode.setRight(sourceNode.right)
}
// Преобразует дерево в строку
toString() {
return this.traverseInOrder().toString()
}
Полный код узла двоичного дерева
import Comparator from '../../utils/comparator'
import HashTable from '../hash-table'
export default class BinaryTreeNode {
constructor(value = null) {
// Значение
this.value = value
// Левый потомок
this.left = null
// Правый потомок
this.right = null
// Предок
this.parent = null
// Дополнительная информация об узле
this.meta = new HashTable()
// Функция сравнения узлов
this.nodeComparator = new Comparator()
}
// Геттер высоты (глубины) левого поддерева
get leftHeight() {
if (!this.left) {
return 0
}
return this.left.height + 1
}
// Геттер высоты правого поддерева
get rightHeight() {
if (!this.right) {
return 0
}
return this.right.height + 1
}
// Геттер максимальной высоты
get height() {
return Math.max(this.leftHeight, this.rightHeight)
}
// Геттер разницы между высотой левого и правого поддеревьев
// (фактор балансировки)
get balanceFactor() {
return this.leftHeight - this.rightHeight
}
// Геттер дяди
get uncle() {
// Если нет предка, то нет и дяди
if (!this.parent) {
return null
}
// Если нет дедушки, то нет и дяди
if (!this.parent.parent) {
return null
}
// Если у дедушки нет двух потомков, то нет и дяди
if (!this.parent.parent.left || !this.parent.parent.right) {
return null
}
// Выясняем, кто является дядей
// путем сравнения предка с потомком дедушки
if (this.nodeComparator.equal(this.parent, this.parent.parent.left)) {
// Дядя - правый узел
return this.parent.parent.right
}
// Дядя - левый узел
return this.parent.parent.left
}
// Устанавл�ивает значение
setValue(value) {
this.value = value
return this
}
// Устанавливает левого потомок
setLeft(node) {
// Сбрасываем предка левого узла
if (this.left) {
this.left.parent = null
}
// Обновляем левый узел
this.left = node
// Делаем текущий узел предком нового левого узла
if (this.left) {
this.left.parent = this
}
return this
}
// Устанавливает правого потомка
setRight(node) {
// Сбрасываем предка правого узла
if (this.right) {
this.right.parent = null
}
// Обновляем правый узел
this.right = node
// Делаем текущий узел предком нового правого узла
if (this.right) {
this.right.parent = this
}
return this
}
// Удаляет потомка
removeChild(nodeToRemove) {
// Если удаляется левый потомок
if (this.left && this.nodeComparator.equal(this.left, nodeToRemove)) {
this.left = null
return true
}
// Если удаляется правый потомок
if (this.right && this.nodeComparator.equal(this.right, nodeToRemove)) {
this.right = null
return true
}
return false
}
// Заменяет потомка
replaceChild(nodeToReplace, replacementNode) {
if (!nodeToReplace || !replacementNode) {
return false
}
// Если заменяется левый потомок
if (this.left && this.nodeComparator.equal(this.left, nodeToReplace)) {
this.left = replacementNode
return true
}
// Если заменяется правый потомок
if (this.right && this.nodeComparator.equal(this.right, nodeToReplace)) {
this.right = replacementNode
return true
}
return false
}
// Обходит дерево в порядке возрастания ключей (inorder, infix traverse):
// сначала обходится левое поддерево, затем корень, затем правое поддерево
traverseInOrder() {
let result = []
if (this.left) {
result = result.concat(this.left.traverseInOrder())
}
result.push(this.value)
if (this.right) {
result = result.concat(this.right.traverseInOrder())
}
return result
}
// Статический метод копирования узла
static copyNode(sourceNode, targetNode) {
targetNode.setValue(sourceNode.value)
targetNode.setLeft(sourceNode.left)
targetNode.setRight(sourceNode.right)
}
// Преобразует дерево в строку
toString() {
return this.traverseInOrder().toString()
}
}
Проверяем, что код работает, как ожидается
// data-structures/tree/__tests__/binary-tree-node.test.js
import BinaryTreeNode from '../binary-tree-node'
describe('BinaryTreeNode', () => {
it('должен создать узел', () => {
const node = new BinaryTreeNode()
expect(node).toBeDefined()
expect(node.value).toBeNull()
expect(node.left).toBeNull()
expect(node.right).toBeNull()
const leftNode = new BinaryTreeNode(1)
const rightNode = new BinaryTreeNode(3)
const rootNode = new BinaryTreeNode(2)
rootNode.setLeft(leftNode).setRight(rightNode)
expect(rootNode.value).toBe(2)
expect(rootNode.left.value).toBe(1)
expect(rootNode.right.value).toBe(3)
})
it('должен установить предка', () => {
const leftNode = new BinaryTreeNode(1)
const rightNode = new BinaryTreeNode(3)
const rootNode = new BinaryTreeNode(2)
rootNode.setLeft(leftNode).setRight(rightNode)
expect(rootNode.parent).toBeNull()
expect(rootNode.left.parent.value).toBe(2)
expect(rootNode.right.parent.value).toBe(2)
expect(rootNode.right.parent).toEqual(rootNode)
})
it('должен обойти дерево', () => {
const leftNode = new BinaryTreeNode(1)
const rightNode = new BinaryTreeNode(3)
const rootNode = new BinaryTreeNode(2)
rootNode.setLeft(leftNode).setRight(rightNode)
expect(rootNode.traverseInOrder()).toEqual([1, 2, 3])
expect(rootNode.toString()).toBe('1,2,3')
})
it('должен удалить потомков', () => {
const leftNode = new BinaryTreeNode(1)
const rightNode = new BinaryTreeNode(3)
const rootNode = new BinaryTreeNode(2)
rootNode.setLeft(leftNode).setRight(rightNode)
expect(rootNode.traverseInOrder()).toEqual([1, 2, 3])
expect(rootNode.removeChild(rootNode.left)).toBe(true)
expect(rootNode.traverseInOrder()).toEqual([2, 3])
expect(rootNode.removeChild(rootNode.right)).toBe(true)
expect(rootNode.traverseInOrder()).toEqual([2])
expect(rootNode.removeChild(rootNode.right)).toBe(false)
expect(rootNode.traverseInOrder()).toEqual([2])
})
it('должен заменить потомков', () => {
const leftNode = new BinaryTreeNode(1)
const rightNode = new BinaryTreeNode(3)
const rootNode = new BinaryTreeNode(2)
rootNode.setLeft(leftNode).setRight(rightNode)
expect(rootNode.traverseInOrder()).toEqual([1, 2, 3])
const replacementNode = new BinaryTreeNode(5)
rightNode.setRight(replacementNode)
expect(rootNode.traverseInOrder()).toEqual([1, 2, 3, 5])
expect(rootNode.replaceChild(rootNode.right, rootNode.right.right)).toBe(
true,
)
expect(rootNode.right.value).toBe(5)
expect(rootNode.right.right).toBeNull()
expect(rootNode.traverseInOrder()).toEqual([1, 2, 5])
expect(rootNode.replaceChild(rootNode.right, rootNode.right.right)).toBe(
false,
)
expect(rootNode.traverseInOrder()).toEqual([1, 2, 5])
expect(rootNode.replaceChild(rootNode.right, replacementNode)).toBe(true)
expect(rootNode.traverseInOrder()).toEqual([1, 2, 5])
expect(rootNode.replaceChild(rootNode.left, replacementNode)).toBe(true)
expect(rootNode.traverseInOrder()).toEqual([5, 2, 5])
expect(
rootNode.replaceChild(new BinaryTreeNode(), new BinaryTreeNode()),
).toBe(false)
})
it('должен вычислить высоту узлов', () => {
const root = new BinaryTreeNode(1)
const left = new BinaryTreeNode(3)
const right = new BinaryTreeNode(2)
const grandLeft = new BinaryTreeNode(5)
const grandRight = new BinaryTreeNode(6)
const grandGrandLeft = new BinaryTreeNode(7)
expect(root.height).toBe(0)
expect(root.balanceFactor).toBe(0)
root.setLeft(left).setRight(right)
expect(root.height).toBe(1)
expect(left.height).toBe(0)
expect(root.balanceFactor).toBe(0)
left.setLeft(grandLeft).setRight(grandRight)
expect(root.height).toBe(2)
expect(left.height).toBe(1)
expect(grandLeft.height).toBe(0)
expect(grandRight.height).toBe(0)
expect(root.balanceFactor).toBe(1)
grandLeft.setLeft(grandGrandLeft)
expect(root.height).toBe(3)
expect(left.height).toBe(2)
expect(grandLeft.height).toBe(1)
expect(grandRight.height).toBe(0)
expect(grandGrandLeft.height).toBe(0)
expect(root.balanceFactor).toBe(2)
})
it('должен также вычислить высоту правых узлов', () => {
const root = new BinaryTreeNode(1)
const right = new BinaryTreeNode(2)
root.setRight(right)
expect(root.height).toBe(1)
expect(right.height).toBe(0)
expect(root.balanceFactor).toBe(-1)
})
it('должен обнулить левый и правый узлы', () => {
const root = new BinaryTreeNode(2)
const left = new BinaryTreeNode(1)
const right = new BinaryTreeNode(3)
root.setLeft(left)
root.setRight(right)
expect(root.left.value).toBe(1)
expect(root.right.value).toBe(3)
root.setLeft(null)
root.setRight(null)
expect(root.left).toBeNull()
expect(root.right).toBeNull()
})
it('должен добавить объекты', () => {
const obj1 = { key: 'object_1', toString: () => 'object_1' }
const obj2 = { key: 'object_2' }
const node1 = new BinaryTreeNode(obj1)
const node2 = new BinaryTreeNode(obj2)
node1.setLeft(node2)
expect(node1.value).toEqual(obj1)
expect(node2.value).toEqual(obj2)
expect(node1.left.value).toEqual(obj2)
node1.removeChild(node2)
expect(node1.value).toEqual(obj1)
expect(node2.value).toEqual(obj2)
expect(node1.left).toBeNull()
expect(node1.toString()).toBe('object_1')
expect(node2.toString()).toBe('[object Object]')
})
it('должен добавить дополнительную информацию в узлы', () => {
const redNode = new BinaryTreeNode(1)
const blackNode = new BinaryTreeNode(2)
redNode.meta.set('color', 'red')
blackNode.meta.set('color', 'black')
expect(redNode.meta.get('color')).toBe('red')
expect(blackNode.meta.get('color')).toBe('black')
})
it('должен найти правильного дядю', () => {
const grandParent = new BinaryTreeNode('grand-parent')
const parent = new BinaryTreeNode('parent')
const uncle = new BinaryTreeNode('uncle')
const child = new BinaryTreeNode('child')
expect(grandParent.uncle).toBeNull()
expect(parent.uncle).toBeNull()
grandParent.setLeft(parent)
expect(parent.uncle).toBeNull()
expect(child.uncle).toBeNull()
parent.setLeft(child)
expect(child.uncle).toBeNull()
grandParent.setRight(uncle)
expect(parent.uncle).toBeNull()
expect(child.uncle).toBeDefined()
expect(child.uncle).toEqual(uncle)
})
it('должен найти левого дядю', () => {
const grandParent = new BinaryTreeNode('grand-parent')
const parent = new BinaryTreeNode('parent')
const uncle = new BinaryTreeNode('uncle')
const child = new BinaryTreeNode('child')
expect(grandParent.uncle).toBeNull()
expect(parent.uncle).toBeNull()
grandParent.setRight(parent)
expect(parent.uncle).toBeNull()
expect(child.uncle).toBeNull()
parent.setRight(child)
expect(child.uncle).toBeNull()
grandParent.setLeft(uncle)
expect(parent.uncle).toBeNull()
expect(child.uncle).toBeDefined()
expect(child.uncle).toEqual(uncle)
})
it('должен установить значения узла', () => {
const node = new BinaryTreeNode('initial_value')
expect(node.value).toBe('initial_value')
node.setValue('new_value')
expect(node.value).toBe('new_value')
})
it('должен копировать узел', () => {
const root = new BinaryTreeNode('root')
const left = new BinaryTreeNode('left')
const right = new BinaryTreeNode('right')
root.setLeft(left).setRight(right)
expect(root.toString()).toBe('left,root,right')
const newRoot = new BinaryTreeNode('new_root')
const newLeft = new BinaryTreeNode('new_left')
const newRight = new BinaryTreeNode('new_right')
newRoot.setLeft(newLeft).setRight(newRight)
expect(newRoot.toString()).toBe('new_left,new_root,new_right')
BinaryTreeNode.copyNode(root, newRoot)
expect(root.toString()).toBe('left,root,right')
expect(newRoot.toString()).toBe('left,root,right')
})
})
Запускаем тесты:
npm run test ./data-structures/tree/__tests__/binary-tree-node.test.js
Результат:

Приступаем к реализации узла двоичного дерева поиска:
// data-structures/tree/binary-search-tree.js
import BinaryTreeNode from './binary-tree-node'
import Comparator from '../../utils/comparator'
export class BinarySearchTreeNode extends BinaryTreeNode {
constructor(value = null, fn) {
super(value)
this.compareFn = fn
this.nodeValueComparator = new Comparator(fn)
}
}
Метод добавления значения (узла):
// Добавляет значение (узел)
insert(value) {
// Если значение отсутствует
if (this.nodeValueComparator.equal(this.value, null)) {
this.value = value
return this
}
// Если новое значение меньше текущего
if (this.nodeValueComparator.lessThan(value, this.value)) {
// Если имеется левый потомок,
if (this.left) {
// добавляем значение в него
return this.left.insert(value)
}
// Создаем новый узел
const newNode = new BinarySearchTreeNode(value, this.compareFn)
// и делаем его левым потомком
this.setLeft(newNode)
return newNode
}
// Если новое значение больше текущего
if (this.nodeValueComparator.greaterThan(value, this.value)) {
// Если имеется правый потомок,
if (this.right) {
// добавляем значение в него
return this.right.insert(value)
}
// Создаем новый узел
const newNode = new BinarySearchTreeNode(value, this.compareFn)
// и делаем его правым потомком
this.setRight(newNode)
return newNode
}
return this
}
Метод удаления узла по значению:
// Удаляет узел по значению
remove(value) {
// Ищем удаляемый узел
const nodeToRemove = this.find(value)
if (!nodeToRemove) {
return null
}
// Извлекаем предка
const { parent } = nodeToRemove
if (!nodeToRemove.left && !nodeToRemove.right) {
// Узел является листовым, т.е. не имеет потомков
if (parent) {
// У узла есть предок. Просто удаляем указатель на этот узел у предка
parent.removeChild(nodeToRemove)
} else {
// У узла нет предка. Обнуляем значение текущего узла
nodeToRemove.setValue(null)
}
} else if (nodeToRemove.left && nodeToRemove.right) {
// Узел имеет двух потомков.
// Находим следующее большее значение (минимальное значение в правом поддереве)
// и заменяем им значение текущего узла
const nextBiggerNode = nodeToRemove.right.findMin()
if (!this.nodeComparator.equal(nextBiggerNode, nodeToRemove.right)) {
this.remove(nextBiggerNode.value)
nodeToRemove.setValue(nextBiggerNode.value)
} else {
// В случае, когда следующее правое значение является следующим большим значением,
// и этот узел не имеет левого �потомка,
// просто заменяем удаляемый узел правым
nodeToRemove.setValue(nodeToRemove.right.value)
nodeToRemove.setRight(nodeToRemove.right.right)
}
} else {
// Узел имеет одного потомка.
// Делаем этого потомка прямым потомком предка текущего узла
const childNode = nodeToRemove.left || nodeToRemove.right
if (parent) {
parent.replaceChild(nodeToRemove, childNode)
} else {
BinaryTreeNode.copyNode(childNode, nodeToRemove)
}
}
// Обнуляем предка удаленного узла
nodeToRemove.parent = null
return true
}
Методы поиска узла по значению и определения наличия узла в дереве:
// Ищет узел по значению
find(value) {
// Проверяем корень
if (this.nodeValueComparator.equal(this.value, value)) {
return this
}
if (this.nodeValueComparator.lessThan(value, this.value) && this.left) {
// Проверяем левое поддерево
return this.left.find(value)
}
if (this.nodeValueComparator.greaterThan(value, this.value) && this.right) {
// Проверяем правое поддерево
return this.right.find(value)
}
return null
}
// Определяет наличие узла
contains(value) {
return Boolean(this.find(value))
}
Вспомогательный метод поиска минимального значения:
// Ищет узел с минимальным значением (нижний левый)
findMin() {
if (!this.left) {
return this
}
return this.left.findMin()
}
Проверяем, что код работает, как ожидается
// data-structures/tree/__tests__/binary-search-tree-node.test.js
import { BinarySearchTreeNode } from '../binary-search-tree'
describe('BinarySearchTreeNode', () => {
it('должен создать узел', () => {
const bstNode = new BinarySearchTreeNode(2)
expect(bstNode.value).toBe(2)
expect(bstNode.left).toBeNull()
expect(bstNode.right).toBeNull()
})
it('должен установить значение узла', () => {
const bstNode = new BinarySearchTreeNode()
bstNode.insert(1)
expect(bstNode.value).toBe(1)
expect(bstNode.left).toBeNull()
expect(bstNode.right).toBeNull()
})
it('должен добавить узлы в правильном порядке', () => {
const bstNode = new BinarySearchTreeNode(2)
const insertedNode1 = bstNode.insert(1)
expect(insertedNode1.value).toBe(1)
expect(bstNode.toString()).toBe('1,2')
expect(bstNode.contains(1)).toBe(true)
expect(bstNode.contains(3)).toBe(false)
const insertedNode2 = bstNode.insert(3)
expect(insertedNode2.value).toBe(3)
expect(bstNode.toString()).toBe('1,2,3')
expect(bstNode.contains(3)).toBe(true)
expect(bstNode.contains(4)).toBe(false)
bstNode.insert(7)
expect(bstNode.toString()).toBe('1,2,3,7')
expect(bstNode.contains(7)).toBe(true)
expect(bstNode.contains(8)).toBe(false)
bstNode.insert(4)
expect(bstNode.toString()).toBe('1,2,3,4,7')
expect(bstNode.contains(4)).toBe(true)
expect(bstNode.contains(8)).toBe(false)
bstNode.insert(6)
expect(bstNode.toString()).toBe('1,2,3,4,6,7')
expect(bstNode.contains(6)).toBe(true)
expect(bstNode.contains(8)).toBe(false)
})
it('не должен добавлять дубликаты', () => {
const bstNode = new BinarySearchTreeNode(2)
bstNode.insert(1)
expect(bstNode.toString()).toBe('1,2')
expect(bstNode.contains(1)).toBe(true)
expect(bstNode.contains(3)).toBe(false)
bstNode.insert(1)
expect(bstNode.toString()).toBe('1,2')
expect(bstNode.contains(1)).toBe(true)
expect(bstNode.contains(3)).toBe(false)
})
it('должен найти минимальный узел', () => {
const node = new BinarySearchTreeNode(10)
node.insert(20)
node.insert(30)
node.insert(5)
node.insert(40)
node.insert(1)
expect(node.findMin()).not.toBeNull()
expect(node.findMin().value).toBe(1)
})
it('должен добавить дополнительную информацию к узлам', () => {
const node = new BinarySearchTreeNode(10)
node.insert(20)
const node1 = node.insert(30)
node.insert(5)
node.insert(40)
const node2 = node.insert(1)
node.meta.set('color', 'red')
node1.meta.set('color', 'black')
node2.meta.set('color', 'white')
expect(node.meta.get('color')).toBe('red')
expect(node.findMin()).not.toBeNull()
expect(node.findMin().value).toBe(1)
expect(node.findMin().meta.get('color')).toBe('white')
expect(node.find(30).meta.get('color')).toBe('black')
})
it('должен найти узлы', () => {
const node = new BinarySearchTreeNode(10)
node.insert(20)
node.insert(30)
node.insert(5)
node.insert(40)
node.insert(1)
expect(node.find(6)).toBeNull()
expect(node.find(5)).not.toBeNull()
expect(node.find(5).value).toBe(5)
})
it('должен удалить листовые узлы', () => {
const bstRootNode = new BinarySearchTreeNode()
bstRootNode.insert(10)
bstRootNode.insert(20)
bstRootNode.insert(5)
expect(bstRootNode.toString()).toBe('5,10,20')
const removed1 = bstRootNode.remove(5)
expect(bstRootNode.toString()).toBe('10,20')
expect(removed1).toBe(true)
const removed2 = bstRootNode.remove(20)
expect(bstRootNode.toString()).toBe('10')
expect(removed2).toBe(true)
})
it('должен удалить узлы с одним потомком', () => {
const bstRootNode = new BinarySearchTreeNode()
bstRootNode.insert(10)
bstRootNode.insert(20)
bstRootNode.insert(5)
bstRootNode.insert(30)
expect(bstRootNode.toString()).toBe('5,10,20,30')
bstRootNode.remove(20)
expect(bstRootNode.toString()).toBe('5,10,30')
bstRootNode.insert(1)
expect(bstRootNode.toString()).toBe('1,5,10,30')
bstRootNode.remove(5)
expect(bstRootNode.toString()).toBe('1,10,30')
})
it('должен удалить узлы с двумя потомками', () => {
const bstRootNode = new BinarySearchTreeNode()
bstRootNode.insert(10)
bstRootNode.insert(20)
bstRootNode.insert(5)
bstRootNode.insert(30)
bstRootNode.insert(15)
bstRootNode.insert(25)
expect(bstRootNode.toString()).toBe('5,10,15,20,25,30')
expect(bstRootNode.find(20).left.value).toBe(15)
expect(bstRootNode.find(20).right.value).toBe(30)
bstRootNode.remove(20)
expect(bstRootNode.toString()).toBe('5,10,15,25,30')
bstRootNode.remove(15)
expect(bstRootNode.toString()).toBe('5,10,25,30')
bstRootNode.remove(10)
expect(bstRootNode.toString()).toBe('5,25,30')
expect(bstRootNode.value).toBe(25)
bstRootNode.remove(25)
expect(bstRootNode.toString()).toBe('5,30')
bstRootNode.remove(5)
expect(bstRootNode.toString()).toBe('30')
})
it('должен удалить узел без предка', () => {
const bstRootNode = new BinarySearchTreeNode()
expect(bstRootNode.toString()).toBe('')
bstRootNode.insert(1)
bstRootNode.insert(2)
expect(bstRootNode.toString()).toBe('1,2')
bstRootNode.remove(1)
expect(bstRootNode.toString()).toBe('2')
bstRootNode.remove(2)
expect(bstRootNode.toString()).toBe('')
})
it('должен удалить несуществующий узел', () => {
const bstRootNode = new BinarySearchTreeNode()
bstRootNode.insert(10)
bstRootNode.insert(20)
const removedNode = bstRootNode.remove(30)
expect(removedNode).toBeNull()
})
it('должен добавить объекты', () => {
const nodeValueComparatorCallback = (a, b) => {
const normalizedA = a || { value: null }
const normalizedB = b || { value: null }
if (normalizedA.value === normalizedB.value) {
return 0
}
return normalizedA.value < normalizedB.value ? -1 : 1
}
const obj1 = { key: 'obj1', value: 1, toString: () => 'obj1' }
const obj2 = { key: 'obj2', value: 2, toString: () => 'obj2' }
const obj3 = { key: 'obj3', value: 3, toString: () => 'obj3' }
const bstNode = new BinarySearchTreeNode(obj2, nodeValueComparatorCallback)
bstNode.insert(obj1)
expect(bstNode.toString()).toBe('obj1,obj2')
expect(bstNode.contains(obj1)).toBe(true)
expect(bstNode.contains(obj3)).toBe(false)
bstNode.insert(obj3)
expect(bstNode.toString()).toBe('obj1,obj2,obj3')
expect(bstNode.contains(obj3)).toBe(true)
expect(bstNode.findMin().value).toEqual(obj1)
})
it('должен обнулить предка удаленного узла', () => {
const rootNode = new BinarySearchTreeNode('foo')
rootNode.insert('bar')
const childNode = rootNode.find('bar')
rootNode.remove('bar')
expect(childNode.parent).toBeNull()
})
})
Запускаем тесты:
npm run test ./data-structures/tree/__tests__/binary-search-tree-node.test.js
Результат:

Приступаем к реализации двоичного дерева поиска:
// data-structures/tree/binary-search-tree.js
export default class BinarySearchTree {
constructor(compareFn) {
// Корневой узел
this.root = new BinarySearchTreeNode(null, compareFn)
// Функция сравнения узлов
this.nodeComparator = this.root.nodeComparator
}
}
Все необходимые методы дерева нами уже реализованы на уровне узла, остались последние штрихи:
// Добавляет значение (узел)
insert(value) {
return this.root.insert(value)
}
// Удаляет узел по значению
remove(value) {
return this.root.remove(value)
}
// Определяет наличие узла
contains(value) {
return this.root.contains(value)
}
// Возвращает строковое представление дерева
toString() {
return this.root.toString()
}
Полный код узла двоичного дерева поиска и самого дерева
import BinaryTreeNode from './binary-tree-node'
import Comparator from '../../utils/comparator'
export class BinarySearchTreeNode extends BinaryTreeNode {
constructor(value = null, fn) {
super(value)
this.compareFn = fn
this.nodeValueComparator = new Comparator(fn)
}
// Добавляет значение (узел)
insert(value) {
// Если значение отсутствует
if (this.nodeValueComparator.equal(this.value, null)) {
this.value = value
return this
}
// Если новое значение меньше текущего
if (this.nodeValueComparator.lessThan(value, this.value)) {
// Если имеется левый потомок,
if (this.left) {
// добавляем значение в него
return this.left.insert(value)
}
// Создаем новый узел
const newNode = new BinarySearchTreeNode(value, this.compareFn)
// и делаем его левым потомком
this.setLeft(newNode)
return newNode
}
// Если новое значение больше текущего
if (this.nodeValueComparator.greaterThan(value, this.value)) {
// Если имеется правый потомок,
if (this.right) {
// добавляем значение в него
return this.right.insert(value)
}
// Создаем новый узел
const newNode = new BinarySearchTreeNode(value, this.compareFn)
// и делаем его правым потомком
this.setRight(newNode)
return newNode
}
return this
}
// Удаляет узел по значению
remove(value) {
// Ищем удаляемый узел
const nodeToRemove = this.find(value)
if (!nodeToRemove) {
return null
}
// Извлекаем предка
const { parent } = nodeToRemove
if (!nodeToRemove.left && !nodeToRemove.right) {
// Узел является листовым, т.е. не имеет потомков
if (parent) {
// У узла есть предок. Просто удаляем указатель на этот узел у предка
parent.removeChild(nodeToRemove)
} else {
// У узла нет предка. Обнуляем значение текущего узла
nodeToRemove.setValue(null)
}
} else if (nodeToRemove.left && nodeToRemove.right) {
// Узел имеет двух потомков.
// Находим следующее большее значение (минимальное значение в правом поддереве)
// и заменяем им значение текущего узла
const nextBiggerNode = nodeToRemove.right.findMin()
if (!this.nodeComparator.equal(nextBiggerNode, nodeToRemove.right)) {
this.remove(nextBiggerNode.value)
nodeToRemove.setValue(nextBiggerNode.value)
} else {
// В случае, когда следующее правое значение является следующим большим значением,
// и этот узел не имеет левого потомка,
// просто заменяем удаляемый узел правым
nodeToRemove.setValue(nodeToRemove.right.value)
nodeToRemove.setRight(nodeToRemove.right.right)
}
} else {
// Узел имеет одного потомка.
// Делаем этого потомка прямым потомком предка текущего узла
const childNode = nodeToRemove.left || nodeToRemove.right
if (parent) {
parent.replaceChild(nodeToRemove, childNode)
} else {
BinaryTreeNode.copyNode(childNode, nodeToRemove)
}
}
// Обнуляем предка удаленного узла
nodeToRemove.parent = null
return true
}
// Ищет узел по значению
find(value) {
// Проверяем корень
if (this.nodeValueComparator.equal(this.value, value)) {
return this
}
if (this.nodeValueComparator.lessThan(value, this.value) && this.left) {
// Проверяем левое поддерево
return this.left.find(value)
}
if (this.nodeValueComparator.greaterThan(value, this.value) && this.right) {
// Проверяем правое поддерево
return this.right.find(value)
}
return null
}
// Определяет наличие узла
contains(value) {
return Boolean(this.find(value))
}
// Ищет узел с минимальным значением (нижний левый)
findMin() {
if (!this.left) {
return this
}
return this.left.findMin()
}
}
export default class BinarySearchTree {
constructor(compareFn) {
// Корневой узел
this.root = new BinarySearchTreeNode(null, compareFn)
// Функция сравнения узлов
this.nodeComparator = this.root.nodeComparator
}
// Добавляет значение
insert(value) {
return this.root.insert(value)
}
// Удаляет узел по значению
remove(value) {
return this.root.remove(value)
}
// Определяет наличие узла
contains(value) {
return this.root.contains(value)
}
// Возвращает строковое представление дерева
toString() {
return this.root.toString()
}
}
Проверяем, что код работает, как ожидается
// data-structures/tree/__tests__/binary-search-tree.test.js
import BinarySearchTree from '../binary-search-tree'
describe('BinarySearchTree', () => {
it('должен создать дерево', () => {
const bst = new BinarySearchTree()
expect(bst).toBeDefined()
expect(bst.root).toBeDefined()
expect(bst.root.value).toBeNull()
expect(bst.root.left).toBeNull()
expect(bst.root.right).toBeNull()
})
it('должен добавить значения', () => {
const bst = new BinarySearchTree()
const insertedNode1 = bst.insert(10)
const insertedNode2 = bst.insert(20)
bst.insert(5)
expect(bst.toString()).toBe('5,10,20')
expect(insertedNode1.value).toBe(10)
expect(insertedNode2.value).toBe(20)
})
it('должен определить наличие значений', () => {
const bst = new BinarySearchTree()
bst.insert(10)
bst.insert(20)
bst.insert(5)
expect(bst.contains(20)).toBe(true)
expect(bst.contains(40)).toBe(false)
})
it('должен удалить узлы', () => {
const bst = new BinarySearchTree()
bst.insert(10)
bst.insert(20)
bst.insert(5)
expect(bst.toString()).toBe('5,10,20')
const removed1 = bst.remove(5)
expect(bst.toString()).toBe('10,20')
expect(removed1).toBe(true)
const removed2 = bst.remove(20)
expect(bst.toString()).toBe('10')
expect(removed2).toBe(true)
})
it('должен добавить объекты', () => {
const nodeValueCompareFunction = (a, b) => {
const normalizedA = a || { value: null }
const normalizedB = b || { value: null }
if (normalizedA.value === normalizedB.value) {
return 0
}
return normalizedA.value < normalizedB.value ? -1 : 1
}
const obj1 = { key: 'obj1', value: 1, toString: () => 'obj1' }
const obj2 = { key: 'obj2', value: 2, toString: () => 'obj2' }
const obj3 = { key: 'obj3', value: 3, toString: () => 'obj3' }
const bst = new BinarySearchTree(nodeValueCompareFunction)
bst.insert(obj2)
bst.insert(obj3)
bst.insert(obj1)
expect(bst.toString()).toBe('obj1,obj2,obj3')
})
it('должен обойти дерево и вернуть отсортированный массив', () => {
const bst = new BinarySearchTree()
bst.insert(10)
bst.insert(-10)
bst.insert(20)
bst.insert(-20)
bst.insert(25)
bst.insert(6)
expect(bst.toString()).toBe('-20,-10,6,10,20,25')
expect(bst.root.height).toBe(2)
bst.insert(4)
expect(bst.toString()).toBe('-20,-10,4,6,10,20,25')
expect(bst.root.height).toBe(3)
})
})
Запускаем тесты:
npm run test ./data-structures/tree/__tests__/binary-search-tree.test.js
Результат:

АВЛ-дерево
Описание
АВЛ-дерево (AVL tree) - это сбалансированное по высоте двоичное дерево поиска. Для каждой вершины такого дерева высота двух ее поддеревьев не должна различаться более чем на 1. В противном случае, выполняется балансировка дерева путем одного или нескольких поворотов (вращений) смежных узлов.

Анимация добавления нескольких элементов в АВЛ-дерево. Здесь мы наблюдаем левый, правый, правый-левый, левый-правый и правый повороты.

Сбалансированное АВЛ-дерево с факторами баланса (разность между высотой левого и правого поддеревьев).
Вращения (повороты) дерева


Левое вращение.


Правое вращение.


Левое-правое вращение.


Правое-левое вращение.
Интерактивную визуализации АВЛ-дерева можно посмотреть здесь.
Сложность
Временная
| Поиск | Вставка | Удаление |
|---|---|---|
O(log n) | O(log n) | O(log n) |
Пространственная
O(n)
Реализация
Приступаем к реализации АВЛ-дерева:
// data-structures/tree/avl-tree.js
import BinarySearchTree from './binary-search-tree'
// АВЛ-дерево расширяет двоичное дерево поиска
export default class AvlTree extends BinarySearchTree {
}
Методы добавления и удаления узлов:
// Добавляет значение (узел)
insert(value) {
// Обычная вставка
super.insert(value)
// Поднимаемся к корню, выполняя балансировку дерева
let currentNode = this.root.find(value)
while (currentNode) {
this.balance(currentNode)
currentNode = currentNode.parent
}
}
// Удаляет узел по значению
remove(value) {
// Обычное удаление
super.remove(value)
// Балансируем дерево, начиная с корня
this.balance(this.root)
}
Метод балансировки дерева:
// Балансирует дерево
balance(node) {
if (node.balanceFactor > 1) {
// Левый поворот
if (node.left.balanceFactor > 0) {
// Левый-левый поворот
this.rotateLeftLeft(node)
} else if (node.left.balanceFactor < 0) {
// Левый-правый поворот
this.rotateLeftRight(node)
}
} else if (node.balanceFactor < -1) {
// Правый поворот
if (node.right.balanceFactor < 0) {
// Правый-правый поворот
this.rotateRightRight(node)
} else if (node.right.balanceFactor > 0) {
// Правый-левый поворот
this.rotateRightLeft(node)
}
}
}
Методы поворотов (вращений):
// Выполняет левый-левый поворот
rotateLeftLeft(rootNode) {
// Удаляем левого потомка
const leftNode = rootNode.left
rootNode.setLeft(null)
// Делаем левый узел потомком предка `rootNode`
if (rootNode.parent) {
rootNode.parent.setLeft(leftNode)
} else if (rootNode === this.root) {
// Если `rootNode` является корнем, делаем левый узел новым корнем
this.root = leftNode
}
// Если левый узел имеет правого потомка,
// делаем его левым потомком `rootNode`
if (leftNode.right) {
rootNode.setLeft(leftNode.right)
}
// Делаем `rootNode` правым потомком левого узла
leftNode.setRight(rootNode)
}
// Выполняет левый-правый поворот
rotateLeftRight(rootNode) {
// Удаляем левого потомка
const leftNode = rootNode.left
rootNode.setLeft(null)
// Удаляем правого потомка левого узла
const leftRightNode = leftNode.right
leftNode.setRight(null)
// Сохраняем левое поддерево `leftRightNode`
if (leftRightNode.left) {
leftNode.setRight(leftRightNode.left)
leftRightNode.setLeft(null)
}
rootNode.setLeft(leftRightNode)
leftRightNode.setLeft(leftNode)
// Выполняем левый-левый поворот
this.rotateLeftLeft(rootNode)
}
// Выполняет правый-правый поворот
rotateRightRight(rootNode) {
// Удаляем правого потомка
const rightNode = rootNode.right
rootNode.setRight(null)
// Делаем правый узел потомком предка `rootNode`
if (rootNode.parent) {
rootNode.parent.setRight(rightNode)
} else if (rootNode === this.root) {
// Если `rootNode` является корнем, делаем правый узел новым корнем
this.root = rightNode
}
// Если правы�й узел имеет левого потомка,
// делаем его правым потомком `rootNode`
if (rightNode.left) {
rootNode.setRight(rightNode.left)
}
// Делаем `rootNode` левым потомком правого узла
rightNode.setLeft(rootNode)
}
// Выполняет правый-левый поворот
rotateRightLeft(rootNode) {
// Удаляем правого потомка
const rightNode = rootNode.right
rootNode.setRight(null)
// Удаляем левого потомка правого узла
const rightLeftNode = rightNode.left
rightNode.setLeft(null)
// Сохраняем правое поддерево `rightLeftNode`
if (rightLeftNode.right) {
rightNode.setLeft(rightLeftNode.right)
rightLeftNode.setRight(null)
}
rootNode.setRight(rightLeftNode)
rightLeftNode.setRight(rightNode)
// Выполняем правый-правый поворот
this.rotateRightRight(rootNode)
}
Полный код АВЛ-дерева
import BinarySearchTree from './binary-search-tree'
// АВЛ-дерево расширяет двоичное дерево поиска
export default class AvlTree extends BinarySearchTree {
// Добавляет значение (узел)
insert(value) {
// Обычная вставка
super.insert(value)
// Поднимаемся к корню, выполняя балансировку дерева
let currentNode = this.root.find(value)
while (currentNode) {
this.balance(currentNode)
currentNode = currentNode.parent
}
}
// Удаляет узел по значению
remove(value) {
// Обычное удаление
super.remove(value)
// Балансируем дерево, начиная с корня
this.balance(this.root)
}
// Балансирует дерево
balance(node) {
if (node.balanceFactor > 1) {
// Левый поворот
if (node.left.balanceFactor > 0) {
// Левый-левый поворот
this.rotateLeftLeft(node)
} else if (node.left.balanceFactor < 0) {
// Левый-правый поворот
this.rotateLeftRight(node)
}
} else if (node.balanceFactor < -1) {
// Правый поворот
if (node.right.balanceFactor < 0) {
// Правый-правый поворот
this.rotateRightRight(node)
} else if (node.right.balanceFactor > 0) {
// Правый-левый поворот
this.rotateRightLeft(node)
}
}
}
// Выполняет левый-левый поворот
rotateLeftLeft(rootNode) {
// Удаляем левого потомка
const leftNode = rootNode.left
rootNode.setLeft(null)
// Делаем левый узел потомком предка `rootNode`
if (rootNode.parent) {
rootNode.parent.setLeft(leftNode)
} else if (rootNode === this.root) {
// Если `rootNode` является корнем, делаем левый узел новым корнем
this.root = leftNode
}
// Если левый узел имеет правого потомка,
// делаем его левым потомком `rootNode`
if (leftNode.right) {
rootNode.setLeft(leftNode.right)
}
// Делаем `rootNode` правым потомком левого узла
leftNode.setRight(rootNode)
}
// Выполняет левый-правый поворот
rotateLeftRight(rootNode) {
// Удаляем левого потомка
const leftNode = rootNode.left
rootNode.setLeft(null)
// Удаляем правого потомка левого узла
const leftRightNode = leftNode.right
leftNode.setRight(null)
// Сохраняем левое поддерево `leftRightNode`
if (leftRightNode.left) {
leftNode.setRight(leftRightNode.left)
leftRightNode.setLeft(null)
}
rootNode.setLeft(leftRightNode)
leftRightNode.setLeft(leftNode)
// Выполняем левый-левый поворот
this.rotateLeftLeft(rootNode)
}
// Выполняет правый-правый поворот
rotateRightRight(rootNode) {
// Удаляем правого потомка
const rightNode = rootNode.right
rootNode.setRight(null)
// Делаем правый узел потомком предка `rootNode`
if (rootNode.parent) {
rootNode.parent.setRight(rightNode)
} else if (rootNode === this.root) {
// Если `rootNode` является корнем, делаем правый узел новым корнем
this.root = rightNode
}
// Если правый узел имеет левого потомка,
// делаем его правым потомком `rootNode`
if (rightNode.left) {
rootNode.setRight(rightNode.left)
}
// Делаем `rootNode` левым потомком правого узла
rightNode.setLeft(rootNode)
}
// Выполняет правый-левый поворот
rotateRightLeft(rootNode) {
// Удаляем правого потомка
const rightNode = rootNode.right
rootNode.setRight(null)
// Удаляем левого потомка правого узла
const rightLeftNode = rightNode.left
rightNode.setLeft(null)
// Сохраняем правое поддерево `rightLeftNode`
if (rightLeftNode.right) {
rightNode.setLeft(rightLeftNode.right)
rightLeftNode.setRight(null)
}
rootNode.setRight(rightLeftNode)
rightLeftNode.setRight(rightNode)
// Выполняем правый-правый поворот
this.rotateRightRight(rootNode)
}
}
Тестирование
Проверяем, что код работает, как ожидается
// data-structures/tree/__tests__/avl-tree.test.js
import AvlTree from '../avl-tree'
describe('AvlTree', () => {
it('должен выполнить простой левый-левый поворот', () => {
const tree = new AvlTree()
tree.insert(4)
tree.insert(3)
tree.insert(2)
expect(tree.toString()).toBe('2,3,4')
expect(tree.root.value).toBe(3)
expect(tree.root.height).toBe(1)
tree.insert(1)
expect(tree.toString()).toBe('1,2,3,4')
expect(tree.root.value).toBe(3)
expect(tree.root.height).toBe(2)
tree.insert(0)
expect(tree.toString()).toBe('0,1,2,3,4')
expect(tree.root.value).toBe(3)
expect(tree.root.left.value).toBe(1)
expect(tree.root.height).toBe(2)
})
it('должен выполнить сложный левый-левый поворот', () => {
const tree = new AvlTree()
tree.insert(30)
tree.insert(20)
tree.insert(40)
tree.insert(10)
expect(tree.root.value).toBe(30)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('10,20,30,40')
tree.insert(25)
expect(tree.root.value).toBe(30)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('10,20,25,30,40')
tree.insert(5)
expect(tree.root.value).toBe(20)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('5,10,20,25,30,40')
})
it('должен выполнить простой правый-правый поворот', () => {
const tree = new AvlTree()
tree.insert(2)
tree.insert(3)
tree.insert(4)
expect(tree.toString()).toBe('2,3,4')
expect(tree.root.value).toBe(3)
expect(tree.root.height).toBe(1)
tree.insert(5)
expect(tree.toString()).toBe('2,3,4,5')
expect(tree.root.value).toBe(3)
expect(tree.root.height).toBe(2)
tree.insert(6)
expect(tree.toString()).toBe('2,3,4,5,6')
expect(tree.root.value).toBe(3)
expect(tree.root.right.value).toBe(5)
expect(tree.root.height).toBe(2)
})
it('должен выполнить сложный правый-правый поворот', () => {
const tree = new AvlTree()
tree.insert(30)
tree.insert(20)
tree.insert(40)
tree.insert(50)
expect(tree.root.value).toBe(30)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('20,30,40,50')
tree.insert(35)
expect(tree.root.value).toBe(30)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('20,30,35,40,50')
tree.insert(55)
expect(tree.root.value).toBe(40)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('20,30,35,40,50,55')
})
it('должен выполнить левый-правый поворот', () => {
const tree = new AvlTree()
tree.insert(30)
tree.insert(20)
tree.insert(25)
expect(tree.root.height).toBe(1)
expect(tree.root.value).toBe(25)
expect(tree.toString()).toBe('20,25,30')
})
it('должен выполнить правый-левый поворот', () => {
const tree = new AvlTree()
tree.insert(30)
tree.insert(40)
tree.insert(35)
expect(tree.root.height).toBe(1)
expect(tree.root.value).toBe(35)
expect(tree.toString()).toBe('30,35,40')
})
it('должен создать сбалансированное дерево: кейс #1', () => {
// @see: https://www.youtube.com/watch?v=rbg7Qf8GkQ4&t=839s
const tree = new AvlTree()
tree.insert(1)
tree.insert(2)
tree.insert(3)
expect(tree.root.value).toBe(2)
expect(tree.root.height).toBe(1)
expect(tree.toString()).toBe('1,2,3')
tree.insert(6)
expect(tree.root.value).toBe(2)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('1,2,3,6')
tree.insert(15)
expect(tree.root.value).toBe(2)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('1,2,3,6,15')
tree.insert(-2)
expect(tree.root.value).toBe(2)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('-2,1,2,3,6,15')
tree.insert(-5)
expect(tree.root.value).toBe(2)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('-5,-2,1,2,3,6,15')
tree.insert(-8)
expect(tree.root.value).toBe(2)
expect(tree.root.height).toBe(3)
expect(tree.toString()).toBe('-8,-5,-2,1,2,3,6,15')
})
it('должен создат�ь сбалансированное дерево: кейс #2', () => {
// @see https://www.youtube.com/watch?v=7m94k2Qhg68
const tree = new AvlTree()
tree.insert(43)
tree.insert(18)
tree.insert(22)
tree.insert(9)
tree.insert(21)
tree.insert(6)
expect(tree.root.value).toBe(18)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('6,9,18,21,22,43')
tree.insert(8)
expect(tree.root.value).toBe(18)
expect(tree.root.height).toBe(2)
expect(tree.toString()).toBe('6,8,9,18,21,22,43')
})
it('должен выполнить левый-правый поворот с сохранением левого поддерева: кейс #1', () => {
const tree = new AvlTree()
tree.insert(30)
tree.insert(15)
tree.insert(40)
tree.insert(10)
tree.insert(18)
tree.insert(35)
tree.insert(45)
tree.insert(5)
tree.insert(12)
expect(tree.toString()).toBe('5,10,12,15,18,30,35,40,45')
expect(tree.root.height).toBe(3)
tree.insert(11)
expect(tree.toString()).toBe('5,10,11,12,15,18,30,35,40,45')
expect(tree.root.height).toBe(3)
})
it('должен выполнить левый-правый поворот с сохранением левого поддерева: кейс #2', () => {
const tree = new AvlTree()
tree.insert(30)
tree.insert(15)
tree.insert(40)
tree.insert(10)
tree.insert(18)
tree.insert(35)
tree.insert(45)
tree.insert(42)
tree.insert(47)
expect(tree.toString()).toBe('10,15,18,30,35,40,42,45,47')
expect(tree.root.height).toBe(3)
tree.insert(43)
expect(tree.toString()).toBe('10,15,18,30,35,40,42,43,45,47')
expect(tree.root.height).toBe(3)
})
it('должен удалить значения из дерева с правым-правым поворотом', () => {
const tree = new AvlTree()
tree.insert(10)
tree.insert(20)
tree.insert(30)
tree.insert(40)
expect(tree.toString()).toBe('10,20,30,40')
tree.remove(10)
expect(tree.toString()).toBe('20,30,40')
expect(tree.root.value).toBe(30)
expect(tree.root.left.value).toBe(20)
expect(tree.root.right.value).toBe(40)
expect(tree.root.balanceFactor).toBe(0)
})
it('должен удалить значения из дерева с левым-левым поворотом', () => {
const tree = new AvlTree()
tree.insert(10)
tree.insert(20)
tree.insert(30)
tree.insert(5)
expect(tree.toString()).toBe('5,10,20,30')
tree.remove(30)
expect(tree.toString()).toBe('5,10,20')
expect(tree.root.value).toBe(10)
expect(tree.root.left.value).toBe(5)
expect(tree.root.right.value).toBe(20)
expect(tree.root.balanceFactor).toBe(0)
})
it('должен выполнять балансировку дерева после удаления значений', () => {
const tree = new AvlTree()
tree.insert(1)
tree.insert(2)
tree.insert(3)
tree.insert(4)
tree.insert(5)
tree.insert(6)
tree.insert(7)
tree.insert(8)
tree.insert(9)
expect(tree.toString()).toBe('1,2,3,4,5,6,7,8,9')
expect(tree.root.value).toBe(4)
expect(tree.root.height).toBe(3)
expect(tree.root.balanceFactor).toBe(-1)
tree.remove(8)
expect(tree.root.value).toBe(4)
expect(tree.root.balanceFactor).toBe(-1)
tree.remove(9)
expect(tree.contains(8)).toBeFalsy()
expect(tree.contains(9)).toBeFalsy()
expect(tree.toString()).toBe('1,2,3,4,5,6,7')
expect(tree.root.value).toBe(4)
expect(tree.root.height).toBe(2)
expect(tree.root.balanceFactor).toBe(0)
})
})
Запускаем тесты:
npm run test ./data-structures/tree/__tests__/avl-tree.test.js
Результат:

Красно-черное дерево
Описание
Красно-черное дерево (red-black tree) (КЧД) - это один из видов самобалансирующихся двоичных деревьев поиска. Каждый узел дерева содержит дополнительный бит информации, который часто интерпретируется как цвет (красный или черный) узла. Эти цветовые биты используются для обеспечения относительной сбалансированности дерева при вставке и удалении узлов.
Баланс дерева достигается за счет окрашивания узлов в один их двух цветов способом, который удовлетворяет определенным условиям. Эти условия ограничивают то, насколько несбалансированным может быть дерево (в худшем случае). При модификации дерева, оно перестраивается и перекрашивается для восстановления необходимых свойств. Свойства определены таким образом, чтобы перестановка и перекраска могли выполняться эффективно.

Свойства дерева
В дополнение к требованиям к двоичному дереву поиска, КЧД должно соответствовать следующим критериям:
- каждый узел либо красный, либо черный
- корневой узел черный. Это правило иногда опускается. Поскольку корень всегда может быть перекрашен из красного в черный, но необязательно обратно, это правило слабо влияет на работу дерева
- все листовые узлы (NIL) черные
- если узел красный, оба его потомка черные
- любой путь от определенного узла к любому потомку NIL содержит одинаковое количество черных узлов
Количество черных узлов всех путей от корня к листьям называется черной высотой КЧД.
Эти ограничения обеспечивают критически важное свойство КЧД: путь от корня к самому далекому листу не более, чем в 2 раза длиннее пути от корня к ближайшему листу. Результатом является примерная сбалансированность дерева. Поскольку операции вставки, удаления и поиска узла в КЧД занимают время, пропорциональное высоте дерева (в худшем случае), они являются более эффективными, чем аналогичные операции в обычном двоичном дереве поиска (опять же в худшем случае).
Балансировка дерева в процессе вставки узлов
Если дядя красный

Если дядя черный
- левый-левый случай (
p- левый потомокg,x- левый потомокp) - правый-левый случай (
p- левый потомокg,x- правый потомокp) - правый-правый случай (
p- правый потомокg,x- правый потомокp) - правый-левый случай (
p- правый потомокg,x- левый потомокp)
Левый-левый случай

Левый-правый случай

Правый-правый случай

Правый-левый случай

Интерактивную визуализации КЧД можно посмотреть здесь.
Сложность
Временная
| Поиск | Вставка | Удаление |
|---|---|---|
O(log n) | O(log n) | O(log n) |
Пространственная
O(n)
Реализация
В рамках статьи мы реализуем только вставку новых узлов и балансировку дерева. В конце раздела будет приведена ссылка на более полную реализацию КЧД.
Приступаем к реализации:
// data-structures/tree/red-black-tree.js
import BinarySearchTree from './binary-search-tree'
// Цвета
const COLORS = {
red: 'red',
black: 'black',
}
// Название поля, в котором хранится цвет
const PROP = 'color'
// Красно-черное дерево расширяет двоичное дерево поиска
export default class RedBlackTree extends BinarySearchTree {
}
Метод вставки значения (узла):
// Вставляет значение (узел)
insert(value) {
// Обычная вставка
const insertedNode = super.insert(value)
// Если добавляется корень,
// if (!this.root.left && !this.root.right) {
if (this.nodeComparator.equal(this.root, insertedNode)) {
// делаем его черным
this.makeNodeBlack(insertedNode)
} else {
// Делаем новый узел красным
this.makeNodeRed(insertedNode)
}
// Выполняем балансировку дерева
this.balance(insertedNode)
// Возвращаем добавленный узел
return insertedNode
}
Метод балансировки дерева:
// Выполняет балансировку дерева
balance(node) {
// В случае корневого узла балансировать нечего
if (this.nodeComparator.equal(this.root, node)) return
// В случае черного предка балансировать нечего
if (this.isNodeBlack(node.parent)) return
const grandParent = node.parent.parent
// Если у узла есть красный дядя, то нужно выполнить перекрашивание
if (node.uncle && this.isNodeRed(node.uncle)) {
// Перекрашиваем предка и дядю в черный
this.makeNodeBlack(node.parent)
this.makeNodeBlack(node.uncle)
if (!this.nodeComparator.equal(this.root, grandParent)) {
// Перекрашиваем дедушку в красный, если он не является корнем
this.makeNodeRed(grandParent)
} else {
// Если дедушка - черный корень, ничего не делаем,
// поскольку корень уже имеет двух черных потоков,
// которых мы только что перекрасили
return
}
// Выполняем б�алансировку для перекрашенного дедушки
this.balance(grandParent)
// Если дядя узла черный или отсутствует, нужно выполнить повороты
} else if (!node.uncle || this.isNodeBlack(node.uncle)) {
if (grandParent) {
// Дедушка, которого мы получим после вращений
let newGrandParent
if (this.nodeComparator.equal(node.parent, grandParent.left)) {
// Левый поворот
if (this.nodeComparator.equal(node, grandParent.left.left)) {
// Левый-левый поворот
newGrandParent = this.leftLeftRotation(grandParent)
} else {
// Левый-правый поворот
newGrandParent = this.leftRightRotation(grandParent)
}
} else {
// Правый поворот
if (this.nodeComparator.equal(node, grandParent.right.right)) {
// Правый-правый поворот
newGrandParent = this.rightRightRotation(grandParent)
} else {
// Правый-левый поворот
newGrandParent = this.rightLeftRotation(grandParent)
}
}
// Если `newGrandParent` не имеет предка, делаем его корнем
// и красим в черный
if (newGrandParent && !newGrandParent.parent) {
this.root = newGrandParent
this.makeNodeBlack(this.root)
}
// Выполняем балансировку для нового дедушки
this.balance(newGrandParent)
}
}
}
Методы вращений (поворотов):
// Выполняет левый-левый поворот
leftLeftRotation(grandParentNode) {
// Сохраняем предка дедушки
const grandGrandParent = grandParentNode.parent
// Определяем тип дедушки (левый или правый)
let grandParentNodeIsLeft
if (grandGrandParent) {
grandParentNodeIsLeft = this.nodeComparator.equal(
grandGrandParent.left,
grandParentNode,
)
}
// Сохраняем левого потомка дедушки
const parentNode = grandParentNode.left
// Сохраняем правого потомка предка
const parentRightNode = parentNode.right
// Делаем дедушку правым потомком предка
parentNode.setRight(grandParentNode)
// Делаем правого потомка предка левым потомком дедушки
grandParentNode.setLeft(parentRightNode)
// Заменяем дедушку предком
if (grandGrandParent) {
if (grandParentNodeIsLeft) {
grandGrandParent.setLeft(parentNode)
} else {
grandGrandParent.setRight(parentNode)
}
} else {
// Делаем предка корнем
parentNode.parent = null
}
// Перекрашиваем дедушку и предка
this.swapNodeColors(parentNode, grandParentNode)
// Возвращаем новый корень
return parentNode
}
// Выполняет левый-правый поворот
leftRightRotation(grandParentNode) {
// Сохраняем левый и левый правый узлы
const parentNode = grandParentNode.left
const childNode = parentNode.right
// Сохраняем левый узел потомка во избежание потери
// левого поддерева. Позже он будет перемещен в
// правое поддерево предка
const childLeftNode = childNode.left
// Делаем предка левым узлом потомка
childNode.setLeft(parentNode)
// Делаем левый узел потомка правым узлом предка
parentNode.setRight(childLeftNode)
// Помещаем левый правый узел на место левого
grandParentNode.setLeft(childNode)
// Выполняем левый-левый поворот
return this.leftLeftRotation(grandParentNode)
}
// Выполняет правый-правый поворот
rightRightRotation(grandParentNode) {
// Сохраняем предка дедушки
const grandGrandParent = grandParentNode.parent
// Определяем тип дедушки (левый или правый)
let grandParentNodeIsLeft
if (grandGrandParent) {
grandParentNodeIsLeft = this.nodeComparator.equal(
grandGrandParent.left,
grandParentNode,
)
}
// Сохраняем правого потомка дедушки
const parentNode = grandParentNode.right
// Сохраняем левого потомка предка
const parentLeftNode = parentNode.left
// Делаем дедушку левым потомком предка
parentNode.setLeft(grandParentNode)
// Делаем левого потомка предка правым потомком дедушки
grandParentNode.setRight(parentLeftNode)
// Заменяем дедушку предком
if (grandGrandParent) {
if (grandParentNodeIsLeft) {
grandGrandParent.setLeft(parentNode)
} else {
grandGrandParent.setRight(parentNode)
}
} else {
// Делаем предка корнем
parentNode.parent = null
}
// Перекрашиваем дедушку и предка
this.swapNodeColors(parentNode, grandParentNode)
// Возвращаем новый корень
return parentNode
}
// Выполняет правый-левый поворот
rightLeftRotation(grandParentNode) {
// Сохраняем правый и правый левый узлы
const parentNode = grandParentNode.right
const childNode = parentNode.left
// Сохраняем правый узел потомка во избежание потери
// правого поддерева. Позже он будет перемещен в
// левое поддерево предка
const childRightNode = childNode.right
// Делаем предка правым узлом потомка
childNode.setRight(parentNode)
// Делаем правый узел потомка левым узлом предка
parentNode.setLeft(childRightNode)
// Помещаем потомка на место предка
grandParentNode.setRight(childNode)
// Выполняем правый-правый поворот
return this.rightRightRotation(grandParentNode)
}
Напоследок, реализуем несколько вспомогательных методов:
// Делает узел красным
makeNodeRed(node) {
node.meta.set(PROP, COLORS.red)
return node
}
// Делает узел черным
makeNodeBlack(node) {
node.meta.set(PROP, COLORS.black)
return node
}
// Проверяет, является ли узел красным
isNodeRed(node) {
return node.meta.get(PROP) === COLORS.red
}
// Проверяет, является ли узел черным
isNodeBlack(node) {
return node.meta.get(PROP) === COLORS.black
}
// Проверяет, окрашен ли узел
isNodeColored(node) {
return this.isNodeBlack(node) || this.isNodeRed(node)
}
// Перекрашивает узлы
swapNodeColors(node1, node2) {
const node1Color = node1.meta.get(PROP)
const node2Color = node2.meta.get(PROP)
node1.meta.set(PROP, node2Color)
node2.meta.set(PROP, node1Color)
}
Полный код красно-черного дерева
import BinarySearchTree from './binary-search-tree'
// Цвета
const COLORS = {
red: 'red',
black: 'black',
}
// Название поля, в котором хранится цвет
const PROP = 'color'
// Красно-черное дерево расширяет двоичное дерево поиска
export default class RedBlackTree extends BinarySearchTree {
// Вставляет значение (узел)
insert(value) {
// Обычная вставка
const insertedNode = super.insert(value)
// Если добавляется корень,
// if (!this.root.left && !this.root.right) {
if (this.nodeComparator.equal(this.root, insertedNode)) {
// делаем его черным
this.makeNodeBlack(insertedNode)
} else {
// Делаем новый узел красным
this.makeNodeRed(insertedNode)
}
// Выполняем балансировку дерева
this.balance(insertedNode)
// Возвращаем добавленный узел
return insertedNode
}
// Удаляет узел
remove(value) {
throw new Error(`Невозможно удалить ${value}. Метод удаления не реализован`)
}
// Выполняет балансировку дерева
balance(node) {
// В случае корневого узла балансировать нечего
if (this.nodeComparator.equal(this.root, node)) return
// В случае черного предка балансировать нечего
if (this.isNodeBlack(node.parent)) return
const grandParent = node.parent.parent
// Если у узла есть красный дядя, то нужно выполнить перекрашивание
if (node.uncle && this.isNodeRed(node.uncle)) {
// Перекрашиваем предка и дядю в черный
this.makeNodeBlack(node.parent)
this.makeNodeBlack(node.uncle)
if (!this.nodeComparator.equal(this.root, grandParent)) {
// Перекрашиваем дедушку в красный, если он не является корнем
this.makeNodeRed(grandParent)
} else {
// Если дедушка - черный корень, ничего не делаем,
// поскольку корень уже имеет двух черных потоков,
// которых мы только что перекрасили
return
}
// Выполняем балансировку для перекрашенного дедушки
this.balance(grandParent)
// Если дядя узла черный или отсутствует, нужно выполнить повороты
} else if (!node.uncle || this.isNodeBlack(node.uncle)) {
if (grandParent) {
// Дедушка, которого мы получим после вращений
let newGrandParent
if (this.nodeComparator.equal(node.parent, grandParent.left)) {
// Левый поворот
if (this.nodeComparator.equal(node, grandParent.left.left)) {
// Левый-левый поворот
newGrandParent = this.leftLeftRotation(grandParent)
} else {
// Левый-правый поворот
newGrandParent = this.leftRightRotation(grandParent)
}
} else {
// Правый поворот
if (this.nodeComparator.equal(node, grandParent.right.right)) {
// Правый-правый поворот
newGrandParent = this.rightRightRotation(grandParent)
} else {
// Правый-левый поворот
newGrandParent = this.rightLeftRotation(grandParent)
}
}
// Если `newGrandParent` не имеет предка, делаем его корнем
// и красим в черный
if (newGrandParent && !newGrandParent.parent) {
this.root = newGrandParent
this.makeNodeBlack(this.root)
}
// Выполняем балансировку для нового дедушки
this.balance(newGrandParent)
}
}
}
// Выполняет левый-левый поворот
leftLeftRotation(grandParentNode) {
// Сохраняем предка дедушки
const grandGrandParent = grandParentNode.parent
// Определяем тип дедушки (левый или правый)
let grandParentNodeIsLeft
if (grandGrandParent) {
grandParentNodeIsLeft = this.nodeComparator.equal(
grandGrandParent.left,
grandParentNode,
)
}
// Сохраняем левого потомка дедушки
const parentNode = grandParentNode.left
// Сохраняем правого потомка предка
const parentRightNode = parentNode.right
// Делаем дедушку правым потомком предка
parentNode.setRight(grandParentNode)
// Делаем правого потомка предка левым потомком дедушки
grandParentNode.setLeft(parentRightNode)
// Заменяем дедушку предком
if (grandGrandParent) {
if (grandParentNodeIsLeft) {
grandGrandParent.setLeft(parentNode)
} else {
grandGrandParent.setRight(parentNode)
}
} else {
// Делаем предка корнем
parentNode.parent = null
}
// Перекрашиваем дедушку и предка
this.swapNodeColors(parentNode, grandParentNode)
// Возвращаем новый корень
return parentNode
}
// Выполняет левый-правый поворот
leftRightRotation(grandParentNode) {
// Сохраняем левый и левый правый узлы
const parentNode = grandParentNode.left
const childNode = parentNode.right
// Сохраняем левый узел потомка во избежание потери
// левого поддерева. Позже он будет перемещен в
// правое поддерево предка
const childLeftNode = childNode.left
// Делаем предка левым узлом потомка
childNode.setLeft(parentNode)
// Делаем левый узел потомка правым узлом предка
parentNode.setRight(childLeftNode)
// Помещаем левый правый узел на место левого
grandParentNode.setLeft(childNode)
// Выполняем левый-левый поворот
return this.leftLeftRotation(grandParentNode)
}
// Выполняет правый-правый поворот
rightRightRotation(grandParentNode) {
// Сохраняем предка дедушки
const grandGrandParent = grandParentNode.parent
// Определяем тип дедушки (левый или правый)
let grandParentNodeIsLeft
if (grandGrandParent) {
grandParentNodeIsLeft = this.nodeComparator.equal(
grandGrandParent.left,
grandParentNode,
)
}
// Сохраняем правого потомка дедушки
const parentNode = grandParentNode.right
// Сохраняем левого потомка предка
const parentLeftNode = parentNode.left
// Делаем дедушку левым потомком предка
parentNode.setLeft(grandParentNode)
// Делаем левого потомка предка правым потомком дедушки
grandParentNode.setRight(parentLeftNode)
// Заменяем дедушку предком
if (grandGrandParent) {
if (grandParentNodeIsLeft) {
grandGrandParent.setLeft(parentNode)
} else {
grandGrandParent.setRight(parentNode)
}
} else {
// Делаем предка корнем
parentNode.parent = null
}
// Перекрашиваем дедушку и предка
this.swapNodeColors(parentNode, grandParentNode)
// Возвращаем новый корень
return parentNode
}
// Выполняет правый-левый поворот
rightLeftRotation(grandParentNode) {
// Сохраняем правый и правый левый узлы
const parentNode = grandParentNode.right
const childNode = parentNode.left
// Сохраняем правый узел потомка во избежание потери
// правого поддерева. Позже он будет перемещен в
// левое поддерево предка
const childRightNode = childNode.right
// Делаем предка правым узлом потомка
childNode.setRight(parentNode)
// Делаем правый узел потомка левым узлом предка
parentNode.setLeft(childRightNode)
// Помещаем потомка на место предка
grandParentNode.setRight(childNode)
// Выполняем правый-правый поворот
return this.rightRightRotation(grandParentNode)
}
// Делает узел красным
makeNodeRed(node) {
node.meta.set(PROP, COLORS.red)
return node
}
// Делает узел черным
makeNodeBlack(node) {
node.meta.set(PROP, COLORS.black)
return node
}
// Проверяет, является ли узел красным
isNodeRed(node) {
return node.meta.get(PROP) === COLORS.red
}
// Проверяет, является ли узел черным
isNodeBlack(node) {
return node.meta.get(PROP) === COLORS.black
}
// Проверяет, покрашен ли узел
isNodeColored(node) {
return this.isNodeBlack(node) || this.isNodeRed(node)
}
// Перекрашивает узлы
swapNodeColors(node1, node2) {
const node1Color = node1.meta.get(PROP)
const node2Color = node2.meta.get(PROP)
node1.meta.set(PROP, node2Color)
node2.meta.set(PROP, node1Color)
}
}
Более полную реализацию (каноническую, учитывая почти 10 млн установок в неделю) красно-черного дерева можно найти здесь.
Тестирование
Проверяем, что наш код работает, как ожидается
// data-structures/tree/__tests__/red-black-tree.test.js
import RedBlackTree from '../red-black-tree'
describe('RedBlackTree', () => {
it('должен покрасить первый узел в черный', () => {
const tree = new RedBlackTree()
const firstInsertedNode = tree.insert(10)
expect(tree.isNodeColored(firstInsertedNode)).toBe(true)
expect(tree.isNodeBlack(firstInsertedNode)).toBe(true)
expect(tree.isNodeRed(firstInsertedNode)).toBe(false)
expect(tree.toString()).toBe('10')
expect(tree.root.height).toBe(0)
})
it('должен окрасить новые листовые узлы в красный', () => {
const tree = new RedBlackTree()
const firstInsertedNode = tree.insert(10)
const secondInsertedNode = tree.insert(15)
const thirdInsertedNode = tree.insert(5)
expect(tree.isNodeBlack(firstInsertedNode)).toBe(true)
expect(tree.isNodeRed(secondInsertedNode)).toBe(true)
expect(tree.isNodeRed(thirdInsertedNode)).toBe(true)
expect(tree.toString()).toBe('5,10,15')
expect(tree.root.height).toBe(1)
})
it('должен выполнить балансировку дерева', () => {
const tree = new RedBlackTree()
tree.insert(5)
tree.insert(10)
tree.insert(15)
tree.insert(20)
tree.insert(25)
tree.insert(30)
expect(tree.toString()).toBe('5,10,15,20,25,30')
expect(tree.root.height).toBe(3)
})
it('должен выполнить балансировку в случае черного предка', () => {
const tree = new RedBlackTree()
const node1 = tree.insert(10)
expect(tree.isNodeBlack(node1)).toBe(true)
const node2 = tree.insert(-10)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeRed(node2)).toBe(true)
const node3 = tree.insert(20)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeRed(node2)).toBe(true)
expect(tree.isNodeRed(node3)).toBe(true)
const node4 = tree.insert(-20)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeBlack(node2)).toBe(true)
expect(tree.isNodeBlack(node3)).toBe(true)
expect(tree.isNodeRed(node4)).toBe(true)
const node5 = tree.insert(25)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeBlack(node2)).toBe(true)
expect(tree.isNodeBlack(node3)).toBe(true)
expect(tree.isNodeRed(node4)).toBe(true)
expect(tree.isNodeRed(node5)).toBe(true)
const node6 = tree.insert(6)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeBlack(node2)).toBe(true)
expect(tree.isNodeBlack(node3)).toBe(true)
expect(tree.isNodeRed(node4)).toBe(true)
expect(tree.isNodeRed(node5)).toBe(true)
expect(tree.isNodeRed(node6)).toBe(true)
expect(tree.toString()).toBe('-20,-10,6,10,20,25')
expect(tree.root.height).toBe(2)
const node7 = tree.insert(4)
expect(tree.root.left.value).toEqual(node2.value)
expect(tree.toString()).toBe('-20,-10,4,6,10,20,25')
expect(tree.root.height).toBe(3)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeRed(node2)).toBe(true)
expect(tree.isNodeBlack(node3)).toBe(true)
expect(tree.isNodeBlack(node4)).toBe(true)
expect(tree.isNodeBlack(node4)).toBe(true)
expect(tree.isNodeRed(node5)).toBe(true)
expect(tree.isNodeBlack(node6)).toBe(true)
expect(tree.isNodeRed(node7)).toBe(true)
})
it('должен выполнить балансировку в случае красного дяди', () => {
const tree = new RedBlackTree()
const node1 = tree.insert(10)
const node2 = tree.insert(-10)
const node3 = tree.insert(20)
const node4 = tree.insert(-20)
const node5 = tree.insert(6)
const node6 = tree.insert(15)
const node7 = tree.insert(25)
const node8 = tree.insert(2)
const node9 = tree.insert(8)
expect(tree.toString()).toBe('-20,-10,2,6,8,10,15,20,25')
expect(tree.root.height).toBe(3)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeRed(node2)).toBe(true)
expect(tree.isNodeBlack(node3)).toBe(true)
expect(tree.isNodeBlack(node4)).toBe(true)
expect(tree.isNodeBlack(node5)).toBe(true)
expect(tree.isNodeRed(node6)).toBe(true)
expect(tree.isNodeRed(node7)).toBe(true)
expect(tree.isNodeRed(node8)).toBe(true)
expect(tree.isNodeRed(node9)).toBe(true)
const node10 = tree.insert(4)
expect(tree.toString()).toBe('-20,-10,2,4,6,8,10,15,20,25')
expect(tree.root.height).toBe(3)
expect(tree.root.value).toBe(node5.value)
expect(tree.isNodeBlack(node5)).toBe(true)
expect(tree.isNodeRed(node1)).toBe(true)
expect(tree.isNodeRed(node2)).toBe(true)
expect(tree.isNodeRed(node10)).toBe(true)
expect(tree.isNodeRed(node6)).toBe(true)
expect(tree.isNodeRed(node7)).toBe(true)
expect(tree.isNodeBlack(node4)).toBe(true)
expect(tree.isNodeBlack(node8)).toBe(true)
expect(tree.isNodeBlack(node9)).toBe(true)
expect(tree.isNodeBlack(node3)).toBe(true)
})
it('должен выполнить левый-левый поворот', () => {
const tree = new RedBlackTree()
const node1 = tree.insert(10)
const node2 = tree.insert(-10)
const node3 = tree.insert(20)
const node4 = tree.insert(7)
const node5 = tree.insert(15)
expect(tree.toString()).toBe('-10,7,10,15,20')
expect(tree.root.height).toBe(2)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeBlack(node2)).toBe(true)
expect(tree.isNodeBlack(node3)).toBe(true)
expect(tree.isNodeRed(node4)).toBe(true)
expect(tree.isNodeRed(node5)).toBe(true)
const node6 = tree.insert(13)
expect(tree.toString()).toBe('-10,7,10,13,15,20')
expect(tree.root.height).toBe(2)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeBlack(node2)).toBe(true)
expect(tree.isNodeBlack(node5)).toBe(true)
expect(tree.isNodeRed(node4)).toBe(true)
expect(tree.isNodeRed(node6)).toBe(true)
expect(tree.isNodeRed(node3)).toBe(true)
})
it('должен выполнить левый-правый поворот', () => {
const tree = new RedBlackTree()
const node1 = tree.insert(10)
const node2 = tree.insert(-10)
const node3 = tree.insert(20)
const node4 = tree.insert(7)
const node5 = tree.insert(15)
expect(tree.toString()).toBe('-10,7,10,15,20')
expect(tree.root.height).toBe(2)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeBlack(node2)).toBe(true)
expect(tree.isNodeBlack(node3)).toBe(true)
expect(tree.isNodeRed(node4)).toBe(true)
expect(tree.isNodeRed(node5)).toBe(true)
const node6 = tree.insert(17)
expect(tree.toString()).toBe('-10,7,10,15,17,20')
expect(tree.root.height).toBe(2)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeBlack(node2)).toBe(true)
expect(tree.isNodeBlack(node6)).toBe(true)
expect(tree.isNodeRed(node4)).toBe(true)
expect(tree.isNodeRed(node5)).toBe(true)
expect(tree.isNodeRed(node3)).toBe(true)
})
it('должен выполнить перекрашивание, левый-левый и левый-правый повороты', () => {
const tree = new RedBlackTree()
const node1 = tree.insert(10)
const node2 = tree.insert(-10)
const node3 = tree.insert(20)
const node4 = tree.insert(-20)
const node5 = tree.insert(6)
const node6 = tree.insert(15)
const node7 = tree.insert(30)
const node8 = tree.insert(1)
const node9 = tree.insert(9)
expect(tree.toString()).toBe('-20,-10,1,6,9,10,15,20,30')
expect(tree.root.height).toBe(3)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeRed(node2)).toBe(true)
expect(tree.isNodeBlack(node3)).toBe(true)
expect(tree.isNodeBlack(node4)).toBe(true)
expect(tree.isNodeBlack(node5)).toBe(true)
expect(tree.isNodeRed(node6)).toBe(true)
expect(tree.isNodeRed(node7)).toBe(true)
expect(tree.isNodeRed(node8)).toBe(true)
expect(tree.isNodeRed(node9)).toBe(true)
tree.insert(4)
expect(tree.toString()).toBe('-20,-10,1,4,6,9,10,15,20,30')
expect(tree.root.height).toBe(3)
})
it('должен выполнить правый-левый поворот', () => {
const tree = new RedBlackTree()
const node1 = tree.insert(10)
const node2 = tree.insert(-10)
const node3 = tree.insert(20)
const node4 = tree.insert(-20)
const node5 = tree.insert(6)
const node6 = tree.insert(30)
expect(tree.toString()).toBe('-20,-10,6,10,20,30')
expect(tree.root.height).toBe(2)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeBlack(node2)).toBe(true)
expect(tree.isNodeBlack(node3)).toBe(true)
expect(tree.isNodeRed(node4)).toBe(true)
expect(tree.isNodeRed(node5)).toBe(true)
expect(tree.isNodeRed(node6)).toBe(true)
const node7 = tree.insert(25)
const rightNode = tree.root.right
const rightLeftNode = rightNode.left
const rightRightNode = rightNode.right
expect(rightNode.value).toBe(node7.value)
expect(rightLeftNode.value).toBe(node3.value)
expect(rightRightNode.value).toBe(node6.value)
expect(tree.toString()).toBe('-20,-10,6,10,20,25,30')
expect(tree.root.height).toBe(2)
expect(tree.isNodeBlack(node1)).toBe(true)
expect(tree.isNodeBlack(node2)).toBe(true)
expect(tree.isNodeBlack(node7)).toBe(true)
expect(tree.isNodeRed(node4)).toBe(true)
expect(tree.isNodeRed(node5)).toBe(true)
expect(tree.isNodeRed(node3)).toBe(true)
expect(tree.isNodeRed(node6)).toBe(true)
})
it('должен выполнить левый-левый поворот с левым дедушкой', () => {
const tree = new RedBlackTree()
tree.insert(20)
tree.insert(15)
tree.insert(25)
tree.insert(10)
tree.insert(5)
expect(tree.toString()).toBe('5,10,15,20,25')
expect(tree.root.height).toBe(2)
})
it('должен выполнить правый-правый поворот с левым дедушкой', () => {
const tree = new RedBlackTree()
tree.insert(20)
tree.insert(15)
tree.insert(25)
tree.insert(17)
tree.insert(19)
expect(tree.toString()).toBe('15,17,19,20,25')
expect(tree.root.height).toBe(2)
})
it('должен выбросить исключение при попытке удалить узел', () => {
const removeNodeFromRedBlackTree = () => {
const tree = new RedBlackTree()
tree.remove(1)
}
expect(removeNodeFromRedBlackTree).toThrowError()
})
})
Запускаем тесты:
npm run test ./data-structures/tree/__tests__/red-black-tree.test.js
Результат:

Дерево отрезков
Описание
Дерево отрезков (сегментов) (segment tree), также известное как статистическое дерево (statistic tree) - это структура данных, которая используется для хранения информации об отрезках (сегментах, диапазонах). Эта структура данных позволяет запрашивать, какой сегмент содержит определенное значение. По сути, дерево отрезков является статичной структурой данных - ее структура не может меняться после создания.
Дерево отрезков - это двоичное дерево (binary tree, см. часть 3, раздел 9). Корень дерева представляет весь массив. Потомки дерева представляют левую и правую половины массива. Аналогично, потомки каждого узла представляют половины массива, соответствующего узлу.
Дерево строится снизу вверх. Значение предка - это значение минимального потомка (или другое значение в зависимости от переданной функции). Построение дерева занимает время O(n log n). Количество операций - это высота дерева и равняется O(n log n). Для выполнения запросов диапазона (range queries) каждый узел разбивает запрос на две части, по одному подзапросу для каждого потомка. Если запрос содержит весь подмассив узла, мы можем вернуть предварительно вычисленное значение узла. Эта оптимизация позволяет добиться O(n log n) операций.


Случаи применения
Дерево отрезков - это структура данных, спроектированная для эффективного выполнения некоторых операций с массивами, особенно, операций, включающих запросы диапазона.
Такие деревья часто применяются в вычислительной геометрии и географических информационных системах.
Наша реализация дерева отрезков будет принимать любую функцию (принимающую два параметра), позволяя выполнять разные запросы диапазона.
Интерактивную визуализацию дере�ва отрезков можно посмотреть здесь.
Сложность
Временная
| Поиск | Запрос диапазона |
|---|---|
O(log(n)) | O(log(n)) |
Пространственная
O(n)
Реализация
Начнем с реализации вспомогательной функции определения того, является ли переданное число результатом возведения числа 2 в какую-либо степень:
// algorithms/math/is-power-of-two.js
export default function isPowerOfTwo(n) {
// 1 (2^0) - это наименьший результат возведения числа 2 в какую-либо степень
if (n < 1) return false
// Выясняем, можем ли мы разделить переданное число на 2 без остатка
let _n = n
while (_n !== 1) {
// Ненулевой остаток свидетельствует о том,
// что переданное число не может быть результатом возведения числа 2
// в какую - либо степень
if (_n % 2 !== 0) return false
_n /= 2
}
return true
}
Напишем тест для этой функции:
// algorithms/math/__tests__/is-power-of-two.test.js
import isPowerOfTwo from '../is-power-of-two'
describe('isPowerOfTwo', () => {
it('должен проверить, является ли переданное число результатом возведения числа 2 в какую-либо степень', () => {
expect(isPowerOfTwo(-1)).toBe(false)
expect(isPowerOfTwo(0)).toBe(false)
expect(isPowerOfTwo(1)).toBe(true)
expect(isPowerOfTwo(2)).toBe(true)
expect(isPowerOfTwo(3)).toBe(false)
expect(isPowerOfTwo(4)).toBe(true)
expect(isPowerOfTwo(5)).toBe(false)
expect(isPowerOfTwo(6)).toBe(false)
expect(isPowerOfTwo(7)).toBe(false)
expect(isPowerOfTwo(8)).toBe(true)
expect(isPowerOfTwo(10)).toBe(false)
expect(isPowerOfTwo(12)).toBe(false)
expect(isPowerOfTwo(16)).toBe(true)
expect(isPowerOfTwo(31)).toBe(false)
expect(isPowerOfTwo(64)).toBe(true)
expect(isPowerOfTwo(1024)).toBe(true)
expect(isPowerOfTwo(1023)).toBe(false)
})
})
Запускаем этот тест:
npm run test ./algorithms/math/__tests__/is-power-of-two
Результат:

Приступаем к реализации дерева:
// data-structures/tree/segment-tree.js
// Функция определения того, является ли переданное число
// результатом возведения числа 2 в какую-либо степень
// (далее - степенью 2)
import isPowerOfTwo from '../../algorithms/math/is-power-of-two'
export default class SegmentTree {
constructor(arr, fn, fb) {
this.arr = arr
// Основная операция
this.fn = fn
// Резервная операция
this.fb = fb
// Инициализируем представление дерева в виде массива
this.tree = this.initTree(arr)
// Строим дерево
this.buildTree()
}
}
Метод инициализации дерева в виде массива:
// Инициализирует представление дерева в виде массива
initTree(arr) {
let treeLength
const arrLength = arr.length
if (isPowerOfTwo(arrLength)) {
// Если длина массива является степенью 2
treeLength = arrLength * 2 - 1
} else {
// Если длина массива не является степенью 2,
// нужно найти следующее число, которое является таковым,
// и использовать его для вычисления длины дерева.
// Это обусловлено тем, что пустые потомки идеального
// бинарного дерева должны быть заполнены `null`
const currentPower = Math.floor(Math.log2(arrLength))
const nextPower = currentPower + 1
const nextPowerOfTwoN = 2 ** nextPower
treeLength = nextPowerOfTwoN * 2 - 1
}
return new Array(treeLength).fill(null)
}
Метод построения дерева:
// Строит дерево
buildTree() {
const leftIndex = 0
const rightIndex = this.arr.length - 1
const position = 0
// Обращаемся к рекурсии
this.buildTreeRecursively(leftIndex, rightIndex, position)
}
// Строит дерево рекурсивно
buildTreeRecursively(leftIndex, rightIndex, position) {
// Если левый и правый индексы совпадают, значит,
// мы закончили деление пополам и добрались до листового узла.
// Значение листа нужно копировать из массива в дерево
if (leftIndex === rightIndex) {
this.tree[position] = this.arr[leftIndex]
return
}
// Делим массив на две равные части и обрабатываем каждую рекурсивно
const middleIndex = Math.floor((leftIndex + rightIndex) / 2)
// Обрабатываем левую половину
this.buildTreeRecursively(
leftIndex,
middleIndex,
this.getLeftChildIndex(position),
)
// Обрабатываем правую половину
this.buildTreeRecursively(
middleIndex + 1,
rightIndex,
this.getRightChildIndex(position),
)
// После заполнения всех листьев,
// мы можем построить дерево снизу вверх
// с помощью переданной функции
this.tree[position] = this.fn(
this.tree[this.getLeftChildIndex(position)],
this.tree[this.getRightChildIndex(position)],
)
}
Метод выполнения запроса диапазона:
// Выполняет запрос диапазона
rangeQuery(queryLeftIndex, queryRightIndex) {
const leftIndex = 0
const rightIndex = this.arr.length - 1
const position = 0
// Обращаемся к рекурсии
return this.rangeQueryRecursively(
queryLeftIndex,
queryRightIndex,
leftIndex,
rightIndex,
position,
)
}
// Выполняет запрос диапазона рекурсивно
rangeQueryRecursively(
queryLeftIndex,
queryRightIndex,
leftIndex,
rightIndex,
position,
) {
if (queryLeftIndex <= leftIndex && queryRightIndex >= rightIndex) {
// Полное перекрытие
return this.tree[position]
}
if (queryLeftIndex > rightIndex || queryRightIndex < leftIndex) {
// Перекрытие отсутствует
return this.fb
}
// Частичное перекрытие
const middleIndex = Math.floor((leftIndex + rightIndex) / 2)
const leftFnResult = this.rangeQueryRecursively(
queryLeftIndex,
queryRightIndex,
leftIndex,
middleIndex,
this.getLeftChildIndex(position),
)
const rightFnResult = this.rangeQueryRecursively(
queryLeftIndex,
queryRightIndex,
middleIndex + 1,
rightIndex,
this.getRightChildIndex(position),
)
// Обрабатываем узлы с помощью переданной функции
// и возвращаем результат
return this.fn(leftFnResult, rightFnResult)
}
Вспомогательные методы получения индексов потомков:
// Возвращает индекс левого потомка
getLeftChildIndex(parentIndex) {
return parentIndex * 2 + 1
}
// Возвращает индекс правого потомка
getRightChildIndex(parentIndex) {
return parentIndex * 2 + 2
}
Полный код дерева отрезков
// Функция определения того, является ли переданное число
// результатом возведения числа 2 в какую-либо степень
// (далее - степенью 2)
import isPowerOfTwo from '../../algorithms/math/is-power-of-two'
export default class SegmentTree {
constructor(arr, fn, fb) {
this.arr = arr
// Основная операция
this.fn = fn
// Резервная операция
this.fb = fb
// Инициализируем представление дерева в виде массива
this.tree = this.initTree(arr)
// Строим дерево
this.buildTree()
}
// Инициализирует представление дерева в виде массива
initTree(arr) {
let treeLength
const arrLength = arr.length
if (isPowerOfTwo(arrLength)) {
// Если длина массива является степенью 2
treeLength = arrLength * 2 - 1
} else {
// Если длина массива не является степенью 2,
// нужно найти следующее число, которое является таковым,
// и использовать его для вычисления длины дерева.
// Это обусловлено тем, что пустые потомки идеального
// бинарного дерева должны быть заполнены `null`
const currentPower = Math.floor(Math.log2(arrLength))
const nextPower = currentPower + 1
const nextPowerOfTwoN = 2 ** nextPower
treeLength = nextPowerOfTwoN * 2 - 1
}
return new Array(treeLength).fill(null)
}
// Строит дерево
buildTree() {
const leftIndex = 0
const rightIndex = this.arr.length - 1
const position = 0
// Обращаемся к рекурсии
this.buildTreeRecursively(leftIndex, rightIndex, position)
}
// Строит дерево рекурсивно
buildTreeRecursively(leftIndex, rightIndex, position) {
// Если левый и правый индексы совпадают, значит,
// мы закончили деление пополам и добрались до листового узла.
// Значение листа нужно копировать из массива в дерево
if (leftIndex === rightIndex) {
this.tree[position] = this.arr[leftIndex]
return
}
// Делим массив на две равные части и обрабатываем каждую рекурсивно
const middleIndex = Math.floor((leftIndex + rightIndex) / 2)
// Обрабатываем левую половину
this.buildTreeRecursively(
leftIndex,
middleIndex,
this.getLeftChildIndex(position),
)
// Обрабатываем правую половину
this.buildTreeRecursively(
middleIndex + 1,
rightIndex,
this.getRightChildIndex(position),
)
// После заполнения всех лис�тьев,
// мы можем построить дерево снизу вверх
// с помощью переданной функции
this.tree[position] = this.fn(
this.tree[this.getLeftChildIndex(position)],
this.tree[this.getRightChildIndex(position)],
)
}
// Выполняет запрос диапазона
rangeQuery(queryLeftIndex, queryRightIndex) {
const leftIndex = 0
const rightIndex = this.arr.length - 1
const position = 0
// Обращаемся к рекурсии
return this.rangeQueryRecursively(
queryLeftIndex,
queryRightIndex,
leftIndex,
rightIndex,
position,
)
}
// Выполняет запрос диапазона рекурсивно
rangeQueryRecursively(
queryLeftIndex,
queryRightIndex,
leftIndex,
rightIndex,
position,
) {
if (queryLeftIndex <= leftIndex && queryRightIndex >= rightIndex) {
// Полное перекрытие
return this.tree[position]
}
if (queryLeftIndex > rightIndex || queryRightIndex < leftIndex) {
// Перекрытие отсутствует
return this.fb
}
// Частичное перекрытие
const middleIndex = Math.floor((leftIndex + rightIndex) / 2)
const leftFnResult = this.rangeQueryRecursively(
queryLeftIndex,
queryRightIndex,
leftIndex,
middleIndex,
this.getLeftChildIndex(position),
)
const rightFnResult = this.rangeQueryRecursively(
queryLeftIndex,
queryRightIndex,
middleIndex + 1,
rightIndex,
this.getRightChildIndex(position),
)
// Обрабатываем узлы с помощью переданной функции
// и возвращаем результат
return this.fn(leftFnResult, rightFnResult)
}
// Возвращает индекс левого потомка
getLeftChildIndex(parentIndex) {
return parentIndex * 2 + 1
}
// Возвращает индекс правого потомка
getRightChildIndex(parentIndex) {
return parentIndex * 2 + 2
}
}
Тестирование
Проверяем, что наш код работает, как ожидается
// data-structures/tree/__tests__/segment-tree.test.js
import SegmentTree from '../segment-tree'
describe('SegmentTree', () => {
it('должен построить дерево для массива #0 с длиной, являющейся степенью 2', () => {
const array = [-1, 2]
const segmentTree = new SegmentTree(array, Math.min, Infinity)
expect(segmentTree.tree).toEqual([-1, -1, 2])
expect(segmentTree.tree.length).toBe(2 * array.length - 1)
})
it('должен построить дерево для массива #1 с длиной, являющейся степень 2', () => {
const array = [-1, 2, 4, 0]
const segmentTree = new SegmentTree(array, Math.min, Infinity)
expect(segmentTree.tree).toEqual([-1, -1, 0, -1, 2, 4, 0])
expect(segmentTree.tree.length).toBe(2 * array.length - 1)
})
it('должен построить дерево для массива #0 с длиной, НЕ являющейся степень 2', () => {
const array = [0, 1, 2]
const segmentTree = new SegmentTree(array, Math.min, Infinity)
expect(segmentTree.tree).toEqual([0, 0, 2, 0, 1, null, null])
expect(segmentTree.tree.length).toBe(2 * 4 - 1)
})
it('должен построить дерево для массива #1 с длиной, НЕ являющейся степень 2', () => {
const array = [-1, 3, 4, 0, 2, 1]
const segmentTree = new SegmentTree(array, Math.min, Infinity)
expect(segmentTree.tree).toEqual([
-1,
-1,
0,
-1,
4,
0,
1,
-1,
3,
null,
null,
0,
2,
null,
null,
])
expect(segmentTree.tree.length).toBe(2 * 8 - 1)
})
it('должен построить максимальное дерево (предок является максимальным потомком)', () => {
const array = [-1, 2, 4, 0]
const segmentTree = new SegmentTree(array, Math.max, -Infinity)
expect(segmentTree.tree).toEqual([4, 2, 4, -1, 2, 4, 0])
expect(segmentTree.tree.length).toBe(2 * array.length - 1)
})
it('должен построить суммарное дерево (редок является суммой потомков)', () => {
const array = [-1, 2, 4, 0]
const segmentTree = new SegmentTree(array, (a, b) => a + b, 0)
expect(segmentTree.tree).toEqual([5, 1, 4, -1, 2, 4, 0])
expect(segmentTree.tree.length).toBe(2 * array.length - 1)
})
it('должен выполнить минимальный запрос диапазона на массиве с длиной, являющейся степенью 2', () => {
const array = [-1, 3, 4, 0, 2, 1]
const segmentTree = new SegmentTree(array, Math.min, Infinity)
expect(segmentTree.rangeQuery(0, 5)).toBe(-1)
expect(segmentTree.rangeQuery(0, 2)).toBe(-1)
expect(segmentTree.rangeQuery(1, 3)).toBe(0)
expect(segmentTree.rangeQuery(2, 4)).toBe(0)
expect(segmentTree.rangeQuery(4, 5)).toBe(1)
expect(segmentTree.rangeQuery(2, 2)).toBe(4)
})
it('должен выполнить минимальный запрос диапазона на массиве с длиной, НЕ являющейся степенью 2', () => {
const array = [-1, 2, 4, 0]
const segmentTree = new SegmentTree(array, Math.min, Infinity)
expect(segmentTree.rangeQuery(0, 4)).toBe(-1)
expect(segmentTree.rangeQuery(0, 1)).toBe(-1)
expect(segmentTree.rangeQuery(1, 3)).toBe(0)
expect(segmentTree.rangeQuery(1, 2)).toBe(2)
expect(segmentTree.rangeQuery(2, 3)).toBe(0)
expect(segmentTree.rangeQuery(2, 2)).toBe(4)
})
it('должен выполнить максимальный запрос диапазона', () => {
const array = [-1, 3, 4, 0, 2, 1]
const segmentTree = new SegmentTree(array, Math.max, -Infinity)
expect(segmentTree.rangeQuery(0, 5)).toBe(4)
expect(segmentTree.rangeQuery(0, 1)).toBe(3)
expect(segmentTree.rangeQuery(1, 3)).toBe(4)
expect(segmentTree.rangeQuery(2, 4)).toBe(4)
expect(segmentTree.rangeQuery(4, 5)).toBe(2)
expect(segmentTree.rangeQuery(3, 3)).toBe(0)
})
it('должен выполнить суммарный запрос диапазона', () => {
const array = [-1, 3, 4, 0, 2, 1]
const segmentTree = new SegmentTree(array, (a, b) => a + b, 0)
expect(segmentTree.rangeQuery(0, 5)).toBe(9)
expect(segmentTree.rangeQuery(0, 1)).toBe(2)
expect(segmentTree.rangeQuery(1, 3)).toBe(7)
expect(segmentTree.rangeQuery(2, 4)).toBe(6)
expect(segmentTree.rangeQuery(4, 5)).toBe(3)
expect(segmentTree.rangeQuery(3, 3)).toBe(0)
})
})
Запускаем тесты:
npm run test ./data-structures/tree/__tests__/segment-tree
Результат:

Дерево Фенвика
Описание
Дерево Фенвика (Fenwick tree) или двоичное индексированное дерево (ДИД, binary indexed tree, BIT) - это структура данных, которая позволяет эффективно обновлять элементы и вычислять их суммы.
По сравнению с обычным массивом, ДИД позволяет достичь лучшего баланса между двумя операциями: обновлением элементов и вычислением суммы элементов. В массиве n чисел можно хранить либо сами числа, либо их суммы. В первом случае вычисление суммы чисел занимает линейное время. Во втором случае обновление элемента занимает линейное время. Противоположные операции выполняются за константное время. ДИД позволяет выполнять обе операции за время O(log n). Это достигается за счет представления чисел в виде дерева, где значением каждого узла является сумма чисел поддерева. Структура дерева позволяет выполнять операции за O(log n) доступов к узлам.
Особенности реализации
ДИД представлено в виде массива. К�аждый узел дерева хранит сумму узлов некоторого поддерева. Размер ДИД равен n, где n - размер исходного массива. В нашей реализации будет использоваться размер n+1 для простоты. Индексация начинается с 1.

Пример получения суммы элементов с помощью ДИД
- каждый узел имеет индекс (синий) и значение по индексу (зеленый)
- при запросе суммы
i, возвращается суммаBITree[i]и всех предковi - индекс предка
iможет быть получен с помощью следующей формулы:parent(i) = i - i & (-i). Данная операция удаляет последний установленный битi. Например, еслиi=12, тоparent(i)вернет8
Анимированный пример создания ДИД для массива [1, 2, 3, 4, 5] путем добавления элементов одного за другим:

Интерактивную визуализацию ДИД можно посмотреть здесь.
Сложность
Временная
| Запрос суммы | Обновление |
|---|---|
O(log(n)) | O(log(n)) |
Пространственная
O(n)
Реализация
Приступаем к реализации дерева Фенвика:
// data-structures/tree/fenwick-tree.js
export default class FenwickTree {
// Конструктор создает дерево Фенвика размера `size`,
// однако, размер дерева `n+1`, потому что индексация начинается с `1`
constructor(size) {
this.size = size
// Заполняем массив нулями
this.tree = new Array(size + 1).fill(0)
}
}
Метод добавления значения к существующему на определенной позиции:
// Прибавляет значение к существующему на указанной позиции
increase(position, value) {
if (position < 1 || position > this.size) {
throw new Error('Позиция находится за пределами разрешенного диапазона')
}
// magic! :D
for (let i = position; i <= this.size; i += i & -i) {
this.tree[i] += value
}
return this
}
Метод получения суммы от индекса 1 до определенной позиции:
// Возвращает сумму от индекса 1 до указанной позиции
query(position) {
if (position < 1 || position > this.size) {
throw new Error('Позиция находится за пределами разрешенного диапазона')
}
let sum = 0
// magic! :D
for (let i = position; i > 0; i -= i & -i) {
sum += this.tree[i]
}
return sum
}
Метод получения суммы между двумя индексами:
// Возвращает сумму от `leftIndex` до `rightIndex`
queryRange(leftIndex, rightIndex) {
if (leftIndex > rightIndex) {
throw new Error('Левый индекс не может превышать правый')
}
if (leftIndex === 1) {
return this.query(rightIndex)
}
return this.query(rightIndex) - this.query(leftIndex - 1)
}
Полный код дерева Фенвика
export default class FenwickTree {
// Конструктор создает дерево Фенвика размера `size`,
// однако, размер дерева `n+1`, потому что индексация начинается с `1`
constructor(size) {
this.size = size
// Заполняем массив нулями
this.tree = new Array(size + 1).fill(0)
}
// Прибавляет значение к существующему на указанной позиции
increase(position, value) {
if (position < 1 || position > this.size) {
throw new Error('Позиция находится за пределами разрешенного диапазона')
}
// magic! :D
for (let i = position; i <= this.size; i += i & -i) {
this.tree[i] += value
}
return this
}
// Возвращает сумму от индекса 1 до указанной позиции
query(position) {
if (position < 1 || position > this.size) {
throw new Error('Позиция находится за пределами разрешенного диапазона')
}
let sum = 0
// magic! :D
for (let i = position; i > 0; i -= i & -i) {
sum += this.tree[i]
}
return sum
}
// Возвращает сумму от `leftIndex` до `rightIndex`
queryRange(leftIndex, rightIndex) {
if (leftIndex > rightIndex) {
throw new Error('�Левый индекс не может превышать правый')
}
if (leftIndex === 1) {
return this.query(rightIndex)
}
return this.query(rightIndex) - this.query(leftIndex - 1)
}
}
Тестирование
Проверяем, что наш код работает, как ожидается
// data-structures/tree/__tests__/fenwick-tree.test.js
import FenwickTree from '../fenwick-tree'
describe('FenwickTree', () => {
it('должен создать деревья правильного размера', () => {
const tree1 = new FenwickTree(5)
expect(tree1.tree.length).toBe(5 + 1)
for (let i = 0; i < 5; i += 1) {
expect(tree1.tree[i]).toBe(0)
}
const tree2 = new FenwickTree(50)
expect(tree2.tree.length).toBe(50 + 1)
})
it('должен создать правильное дерево', () => {
const inputArray = [3, 2, -1, 6, 5, 4, -3, 3, 7, 2, 3]
const tree = new FenwickTree(inputArray.length)
expect(tree.tree.length).toBe(inputArray.length + 1)
inputArray.forEach((value, index) => {
tree.increase(index + 1, value)
})
expect(tree.tree).toEqual([0, 3, 5, -1, 10, 5, 9, -3, 19, 7, 9, 3])
expect(tree.query(1)).toBe(3)
expect(tree.query(2)).toBe(5)
expect(tree.query(3)).toBe(4)
expect(tree.query(4)).toBe(10)
expect(tree.query(5)).toBe(15)
expect(tree.query(6)).toBe(19)
expect(tree.query(7)).toBe(16)
expect(tree.query(8)).toBe(19)
expect(tree.query(9)).toBe(26)
expect(tree.query(10)).toBe(28)
expect(tree.query(11)).toBe(31)
expect(tree.queryRange(1, 1)).toBe(3)
expect(tree.queryRange(1, 2)).toBe(5)
expect(tree.queryRange(2, 4)).toBe(7)
expect(tree.queryRange(6, 9)).toBe(11)
tree.increase(3, 1)
expect(tree.query(1)).toBe(3)
expect(tree.query(2)).toBe(5)
expect(tree.query(3)).toBe(5)
expect(tree.query(4)).toBe(11)
expect(tree.query(5)).toBe(16)
expect(tree.query(6)).toBe(20)
expect(tree.query(7)).toBe(17)
expect(tree.query(8)).toBe(20)
expect(tree.query(9)).toBe(27)
expect(tree.query(10)).toBe(29)
expect(tree.query(11)).toBe(32)
expect(tree.queryRange(1, 1)).toBe(3)
expect(tree.queryRange(1, 2)).toBe(5)
expect(tree.queryRange(2, 4)).toBe(8)
expect(tree.queryRange(6, 9)).toBe(11)
})
it('должен правильно выполнить запросы', () => {
const tree = new FenwickTree(5)
tree.increase(1, 4)
tree.increase(3, 7)
expect(tree.query(1)).toBe(4)
expect(tree.query(3)).toBe(11)
expect(tree.query(5)).toBe(11)
expect(tree.queryRange(2, 3)).toBe(7)
tree.increase(2, 5)
expect(tree.query(5)).toBe(16)
tree.increase(1, 3)
expect(tree.queryRange(1, 1)).toBe(7)
expect(tree.query(5)).toBe(19)
expect(tree.queryRange(1, 5)).toBe(19)
})
it('должен выбросить исключения', () => {
const tree = new FenwickTree(5)
const increaseAtInvalidLowIndex = () => {
tree.increase(0, 1)
}
const increaseAtInvalidHighIndex = () => {
tree.increase(10, 1)
}
const queryInvalidLowIndex = () => {
tree.query(0)
}
const queryInvalidHighIndex = () => {
tree.query(10)
}
const rangeQueryInvalidIndex = () => {
tree.queryRange(3, 2)
}
expect(increaseAtInvalidLowIndex).toThrowError()
expect(increaseAtInvalidHighIndex).toThrowError()
expect(queryInvalidLowIndex).toThrowError()
expect(queryInvalidHighIndex).toThrowError()
expect(rangeQueryInvalidIndex).toThrowError()
})
})
Запускаем тесты:
npm run test ./data-structures/tree/__tests__/fenwick-tree
Результат:

Граф
Описание
Граф (graph) - это абстрактный тип данных, реализующий математические концепции направленного и ненаправленного (ориентированного и неориентированного) графов (соответствующий раздел математики называется теорией графов).
Граф состоит из конечного (потенциально изменяющегося) набора узлов (вершин, точек) (nodes, vertices, points), а также набора ненаправленных или, соответственно, направленных пар этих узлов. Эти пары называются ребрами (арки, линии, стрелки - для направленного графа) (edges, arcs, lines, arrows). Узлы могут быть как частью графа, так и внешними сущностями, представленными целочисленными индексами или ссылками.
Для разных областей применения графы могут различаться направленностью, ограничениями на количество ребер и дополнительными данными о вершинах и ребрах. Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены в виде графов. Например, строение Википедии можно смоделировать при помощи ориентированного графа, в котором вершинами будут выступать статьи, а ребрами - гиперссылки.

Примеры неориентированного и ориентированного графов
Обратите внимание: ребра графа часто имеют вес, который используется для определения "стоимости" пути.
Любопытная визуализация графа.
Реализация
Начнем с реализации узла графа. Для представления ребер узла целесообразно использовать связный список (см. часть 1, раздел 1):
// data-structures/graph/node.js
// Связный список
import LinkedList from '../linked-list'
// Функция сравнения ребер
const edgeComparator = (a, b) => {
if (a.getKey() === b.getKey()) {
return 0
}
return a.getKey() < b.getKey() ? -1 : 1
}
export default class Node {
constructor(value) {
if (!value) {
throw new Error('Узел графа должен иметь значение!')
}
// Значение узла
this.value = value
// Связный список ребер
this.edges = new LinkedList(edgeComparator)
}
}
Методы добавления и удаления ребер:
// Добавляет ребро в список
addEdge(edge) {
this.edges.append(edge)
return this
}
// Удаляет ребро из списка
removeEdge(edge) {
this.edges.remove(edge)
return this
}
// Удаляет все ребра
removeAllEdges() {
this.getEdges().forEach((edge) => {
this.removeEdge(edge)
})
return this
}
Методы получения соседних узлов, ребер, длины и значения узла:
// Возвращает список соседних узлов
getNeighbors() {
const edges = this.edges.toArray()
return edges.map((node) =>
node.value.from === this ? node.value.to : node.value.from,
)
}
// Возвращает список ребер в виде массива значений
getEdges() {
return this.edges.toArray().map((node) => node.value)
}
// Возвращает длину (глубину) узла
getDegree() {
return this.edges.toArray().length
}
// Возвращает значение узла
getKey() {
return this.value
}
Методы определения наличия ребер и соседей:
// Определяет наличие ребра
hasEdge(edge) {
const _edge = this.edges.find({ cb: (node) => node === edge })
return Boolean(_edge)
}
// Определяет наличие соседа
hasNeighbor(node) {
const _node = this.edges.find({
cb: (n) => n.to === node || n.from === node,
})
return Boolean(_node)
}
Метод поиска ребра по узлу:
// Выполняет поиск ребра по узлу
findEdge(node) {
const _node = this.edges.find({
cb: (n) => n.to === node || n.from === node,
})
return _node ? _node.value : null
}
Наконец, вспомогательный метод стрингификации узла:
// Возвращает строковое представление узла.
// Принимает кастомную функцию стрингификации
toString(cb) {
return cb ? cb(this.value) : `${this.value}`
}
Полный код узла графа
// Связный список
import LinkedList from '../linked-list'
// Функция сравнения ребер
const edgeComparator = (a, b) => {
if (a.getKey() === b.getKey()) {
return 0
}
return a.getKey() < b.getKey() ? -1 : 1
}
// Функция преобразования соседних узлов
const convertNeighbors = (node) => {
return node.value.from === this ? node.value.to : node.value.from
}
export default class Node {
constructor(value) {
if (!value) {
throw new Error('Узел графа должен иметь значение!')
}
// Значение узла
this.value = value
// Связный список ребер
this.edges = new LinkedList(edgeComparator)
}
// Добавляет ребро в список
addEdge(edge) {
this.edges.append(edge)
return this
}
// Удаляет ребро из списка
removeEdge(edge) {
this.edges.remove(edge)
return this
}
// Удаляет все ребра
removeAllEdges() {
this.getEdges().forEach((edge) => {
this.removeEdge(edge)
})
return this
}
// Возвращает список соседей
getNeighbors() {
const edges = this.edges.toArray()
return edges.map(convertNeighbors)
}
// Возвращает список ребер в виде массива значений
getEdges() {
return this.edges.toArray().map((node) => node.value)
}
// Возвращает длину (глубину) узла
getDegree() {
return this.edges.toArray().length
}
// Возвращает значение узла
getKey() {
return this.value
}
// Определяет наличие ребра
hasEdge(edge) {
const _edge = this.edges.find({ cb: (node) => node === edge })
return Boolean(_edge)
}
// Определяет наличие соседа
hasNeighbor(node) {
const _node = this.edges.find({
cb: (n) => n.to === node || n.from === node,
})
return Boolean(_node)
}
// Выполняет поиск ребра по узлу
findEdge(node) {
const _node = this.edges.find({
cb: (n) => n.to === node || n.from === node,
})
return _node ? _node.value : null
}
// Возвращает строковое представление узла.
// Принимает кастомную функцию стрингификации
toString(cb) {
return cb ? cb(this.value) : `${this.value}`
}
}
Код ребра графа до неприличия прост, поэтому привожу его целиком:
// data-structures/graph/edge.js
export default class Edge {
constructor(from, to, weight = 0) {
// Начальный узел
this.from = from
// Конечный узел
this.to = to
// Вес ребра
this.weight = weight
}
// Возвращает ключ ребра
getKey() {
const fromKey = this.from.getKey()
const toKey = this.to.getKey()
// Например, `A_B`
return `${fromKey}_${toKey}`
}
// Инвертирует ребро
reverse() {
const tmp = this.from
this.from = this.to
this.to = tmp
return this
}
// Преобразует ребро в строку
toString() {
return this.getKey()
}
}
Проверяем, что код узла работает, как ожидается
// data-structures/graph/__tests__/node.test.js
import Node from '../node'
import Edge from '../edge'
describe('Node', () => {
it('должен выбросить исключение при создании узла без значения', () => {
let node = null
function createEmptyVertex() {
node = new Node()
}
expect(node).toBeNull()
expect(createEmptyVertex).toThrow()
})
it('должен создать узел графа', () => {
const node = new Node('A')
expect(node).toBeDefined()
expect(node.value).toBe('A')
expect(node.toString()).toBe('A')
expect(node.getKey()).toBe('A')
expect(node.edges.toString()).toBe('')
expect(node.getEdges()).toEqual([])
})
it('должен добавить ребра в узел и определить их наличие', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const edgeAB = new Edge(nodeA, nodeB)
nodeA.addEdge(edgeAB)
expect(nodeA.hasEdge(edgeAB)).toBe(true)
expect(nodeB.hasEdge(edgeAB)).toBe(false)
expect(nodeA.getEdges().length).toBe(1)
expect(nodeA.getEdges()[0].toString()).toBe('A_B')
})
it('должен удалить определенные ребра из узла', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeAB = new Edge(nodeA, nodeB)
const edgeAC = new Edge(nodeA, nodeC)
nodeA.addEdge(edgeAB).addEdge(edgeAC)
expect(nodeA.hasEdge(edgeAB)).toBe(true)
expect(nodeB.hasEdge(edgeAB)).toBe(false)
expect(nodeA.hasEdge(edgeAC)).toBe(true)
expect(nodeC.hasEdge(edgeAC)).toBe(false)
expect(nodeA.getEdges().length).toBe(2)
expect(nodeA.getEdges()[0].toString()).toBe('A_B')
expect(nodeA.getEdges()[1].toString()).toBe('A_C')
nodeA.removeEdge(edgeAB)
expect(nodeA.hasEdge(edgeAB)).toBe(false)
expect(nodeA.hasEdge(edgeAC)).toBe(true)
expect(nodeA.getEdges()[0].toString()).toBe('A_C')
nodeA.removeEdge(edgeAC)
expect(nodeA.hasEdge(edgeAB)).toBe(false)
expect(nodeA.hasEdge(edgeAC)).toBe(false)
expect(nodeA.getEdges().length).toBe(0)
})
it('должна удалить все ребра из узла', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeAB = new Edge(nodeA, nodeB)
const edgeAC = new Edge(nodeA, nodeC)
nodeA.addEdge(edgeAB).addEdge(edgeAC)
expect(nodeA.hasEdge(edgeAB)).toBe(true)
expect(nodeB.hasEdge(edgeAB)).toBe(false)
expect(nodeA.hasEdge(edgeAC)).toBe(true)
expect(nodeC.hasEdge(edgeAC)).toBe(false)
expect(nodeA.getEdges().length).toBe(2)
nodeA.removeAllEdges()
expect(nodeA.hasEdge(edgeAB)).toBe(false)
expect(nodeB.hasEdge(edgeAB)).toBe(false)
expect(nodeA.hasEdge(edgeAC)).toBe(false)
expect(nodeC.hasEdge(edgeAC)).toBe(false)
expect(nodeA.getEdges().length).toBe(0)
})
it('должен вернуть соседей узла в случае, если текущий узел является начальным', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeAB = new Edge(nodeA, nodeB)
const edgeAC = new Edge(nodeA, nodeC)
nodeA.addEdge(edgeAB).addEdge(edgeAC)
expect(nodeB.getNeighbors()).toEqual([])
const neighbors = nodeA.getNeighbors()
expect(neighbors.length).toBe(2)
expect(neighbors[0]).toEqual(nodeB)
expect(neighbors[1]).toEqual(nodeC)
})
it('должен вернуть соседей узла в случае, если текущий узел является конечным', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeBA = new Edge(nodeB, nodeA)
const edgeCA = new Edge(nodeC, nodeA)
nodeA.addEdge(edgeBA).addEdge(edgeCA)
expect(nodeB.getNeighbors()).toEqual([])
const neighbors = nodeA.getNeighbors()
expect(neighbors.length).toBe(2)
expect(neighbors[0]).toEqual(nodeB)
expect(neighbors[1]).toEqual(nodeC)
})
it('должен определить наличие соседнего узла', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeAB = new Edge(nodeA, nodeB)
nodeA.addEdge(edgeAB)
expect(nodeA.hasNeighbor(nodeB)).toBe(true)
expect(nodeA.hasNeighbor(nodeC)).toBe(false)
})
it('должен найти ребро по узлу', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeAB = new Edge(nodeA, nodeB)
nodeA.addEdge(edgeAB)
expect(nodeA.findEdge(nodeB)).toEqual(edgeAB)
expect(nodeA.findEdge(nodeC)).toBeNull()
})
it('должен вычислить глубину узла', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
expect(nodeA.getDegree()).toBe(0)
const edgeAB = new Edge(nodeA, nodeB)
nodeA.addEdge(edgeAB)
expect(nodeA.getDegree()).toBe(1)
const edgeBA = new Edge(nodeB, nodeA)
nodeA.addEdge(edgeBA)
expect(nodeA.getDegree()).toBe(2)
nodeA.addEdge(edgeAB)
expect(nodeA.getDegree()).toBe(3)
expect(nodeA.getEdges().length).toEqual(3)
})
})
Запускаем тесты:
npm run test ./data-structures/graph/__tests__/node
Результат:

Проверяем, что код ребра работает, как ожидается
// data-structures/graph/__tests__/edge.test.js
import Edge from '../edge'
import Node from '../node'
describe('Edge', () => {
it('должена создать ребро графа с дефолтным весом', () => {
const from = new Node('A')
const to = new Node('B')
const edge = new Edge(from, to)
expect(edge.getKey()).toBe('A_B')
expect(edge.toString()).toBe('A_B')
expect(edge.from).toEqual(from)
expect(edge.to).toEqual(to)
expect(edge.weight).toEqual(0)
})
it('должена создать граф с указанным весом', () => {
const from = new Node('A')
const to = new Node('B')
const edge = new Edge(from, to, 10)
expect(edge.from).toEqual(from)
expect(edge.to).toEqual(to)
expect(edge.weight).toEqual(10)
})
it('должен инвертировать ребро', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const edge = new Edge(nodeA, nodeB, 10)
expect(edge.from).toEqual(nodeA)
expect(edge.to).toEqual(nodeB)
expect(edge.weight).toEqual(10)
edge.reverse()
expect(edge.from).toEqual(nodeB)
expect(edge.to).toEqual(nodeA)
expect(edge.weight).toEqual(10)
})
})
Запускаем тесты:
npm run test ./data-structures/graph/__tests__/edge
Результат:

Приступаем к реализации графа:
// data-structures/graph/index.js
export default class Graph {
constructor(isDirected = false) {
// Индикатор направленности графа
// (по умолчанию граф является ненаправленным)
this.isDirected = isDirected
// Узлы
this.nodes = {}
// Ребра
this.edges = {}
}
}
Метод добавления узла в граф и несколько "геттеров":
// Добавляет узел в граф
addNode(newNode) {
this.nodes[newNode.getKey()] = newNode
return this
}
// Возвращает узел по ключу
getNodeByKey(key) {
return this.nodes[key]
}
// Возвращает соседние узлы
getNeighbors(node) {
return node.getNeighbors()
}
// Возвращает значения всех узлов
getAllNodes() {
return Object.values(this.nodes)
}
// Возвращает значения всех ребер
getAllEdges() {
return Object.values(this.edges)
}
Методы добавления, удаления и поиска ребер:
// Добавляет ребро в граф
addEdge(newEdge) {
// Пытаемся найти начальную и конечную вершины
let from = this.getNodeByKey(newEdge.from.getKey())
let to = this.getNodeByKey(newEdge.to.getKey())
// Добавляем начальную вершину
if (!from) {
this.addNode(newEdge.from)
from = this.getNodeByKey(newEdge.from.getKey())
}
// Добавляем конечную вершину
if (!to) {
this.addNode(newEdge.to)
to = this.getNodeByKey(newEdge.to.getKey())
}
// Если ребро уже добавлено
if (this.edges[newEdge.getKey()]) {
throw new Error('Ребро уже добавлено!')
} else {
// Добавляем ребро
this.edges[newEdge.getKey()] = newEdge
}
// Добавляем ребро в вершины
if (this.isDirected) {
from.addEdge(newEdge)
} else {
from.addEdge(newEdge)
to.addEdge(newEdge)
}
return this
}
// Удаляет ребро из графа
removeEdge(edge) {
if (this.edges[edge.getKey()]) {
// Удаляем ребро
delete this.edges[edge.getKey()]
} else {
throw new Error('Ребро не найдено!')
}
// Пытаемся найти начальную и конечную вершины
let from = this.getNodeByKey(edge.from.getKey())
let to = this.getNodeByKey(edge.to.getKey())
// Удаляем ребро из вершин
from && from.removeEdge(edge)
to && to.removeEdge(edge)
}
// Находит ребро в графе
findEdge(from, to) {
// Находим узел по начальному ключу
const node = this.getNodeByKey(from.getKey())
if (!node) return null
// Пытаемся найти конечное ребро
return node.findEdge(to)
}
Методы получения веса графа, инвертирования графа и получения индексов узлов:
// Возвращает вес графа
getWeight() {
// Суммируем веса всех ребер
return this.getAllEdges().reduce((acc, edge) => acc + edge.weight, 0)
}
// Инвертирует граф
reverse() {
// Для каждого ребра
this.getAllEdges().forEach((edge) => {
// Удаляем ребро из графа
this.removeEdge(edge)
// Инвертируем ребро
edge.reverse()
// Снова добавляем ребро в граф
this.addEdge(edge)
})
return this
}
// Возвращает индексы узлов в виде объекта
getNodesIndices() {
const indices = {}
this.getAllNodes().forEach((node, index) => {
indices[node.getKey()] = index
})
return indices
}
Метод получения матрицы смежности:
// Возвращает матрицу смежности
getAdjacencyMatrix() {
// Узлы
const nodes = this.getAllNodes()
// Индексы узлов
const indices = this.getNodesIndices()
// Инициализируем матрицу смежности (заполняем ее `null`)
const matrix = new Array(nodes.length)
.fill()
.map(() => new Array(nodes.length).fill(null))
// Формируем матрицу.
// Перебираем узлы
nodes.forEach((node, index) => {
// Перебираем соседей узла
node.getNeighbors().forEach((neighbor) => {
// Индекс соседа
const neighborIndex = indices[neighbor.getKey()]
// [индекс узла][индекс соседа] = вес ребра
matrix[index][neighborIndex] = this.findEdge(node, neighbor).weight
})
})
return matrix
}
Наконец, вспомогательный метод преобразования графа в строку:
// Возвращает строковое представление графа
toString() {
return Object.keys(this.nodes).toString()
}
Полный код графа
export default class Graph {
constructor(isDirected = false) {
// Индикатор направленности графа
// (по умолчанию граф является ненаправленным)
this.isDirected = isDirected
// Узлы
this.nodes = {}
// Ребра
this.edges = {}
}
// Добавляет узел в граф
addNode(newNode) {
this.nodes[newNode.getKey()] = newNode
return this
}
// Возвращает узел по ключу
getNodeByKey(key) {
return this.nodes[key]
}
// Возвращает соседние узлы
getNeighbors(node) {
return node.getNeighbors()
}
// Возвращает значения всех узлов
getAllNodes() {
return Object.values(this.nodes)
}
// Возвращает значения всех ребер
getAllEdges() {
return Object.values(this.edges)
}
// Добавляет ребро в граф
addEdge(newEdge) {
// Пытаемся найти начальную и конечную вершины
let from = this.getNodeByKey(newEdge.from.getKey())
let to = this.getNodeByKey(newEdge.to.getKey())
// Добавляем начальную вершину
if (!from) {
this.addNode(newEdge.from)
from = this.getNodeByKey(newEdge.from.getKey())
}
// Добавляем конечную вершину
if (!to) {
this.addNode(newEdge.to)
to = this.getNodeByKey(newEdge.to.getKey())
}
// Если ребро уже добавлено
if (this.edges[newEdge.getKey()]) {
throw new Error('Ребро уже добавлено!')
} else {
// Добавляем ребро
this.edges[newEdge.getKey()] = newEdge
}
// Добавляем ребро в вершины
if (this.isDirected) {
from.addEdge(newEdge)
} else {
from.addEdge(newEdge)
to.addEdge(newEdge)
}
return this
}
// Удаляет ребро из графа
removeEdge(edge) {
if (this.edges[edge.getKey()]) {
// Удаляем ребро
delete this.edges[edge.getKey()]
} else {
throw new Error('Ребро не найдено!')
}
// Пытаемся найти начальную и конечную вершины
let from = this.getNodeByKey(edge.from.getKey())
let to = this.getNodeByKey(edge.to.getKey())
// Удаляем ребро из вершин
from && from.removeEdge(edge)
to && to.removeEdge(edge)
}
// Находит ребро в графе
findEdge(from, to) {
// Находим узел по начальному ключу
const node = this.getNodeByKey(from.getKey())
if (!node) return null
// Пытаемся найти конечное ребро
return node.findEdge(to)
}
// Возвращает вес графа
getWeight() {
// Суммируем веса всех ребер
return this.getAllEdges().reduce((acc, edge) => acc + edge.weight, 0)
}
// Инвертирует граф
reverse() {
// Для каждого ребра
this.getAllEdges().forEach((edge) => {
// Удаляем ребро из графа
this.removeEdge(edge)
// Инвертируем ребро
edge.reverse()
// Снова добавляем ребро в граф
this.addEdge(edge)
})
return this
}
// Возвращает индексы узлов в виде объекта
getNodesIndices() {
const indices = {}
this.getAllNodes().forEach((node, index) => {
indices[node.getKey()] = index
})
return indices
}
// Возвращает матрицу смежности
getAdjacencyMatrix() {
// Узлы
const nodes = this.getAllNodes()
// Индексы узлов
const indices = this.getNodesIndices()
// Инициализируем матрицу смежности (заполняем ее `null`)
const matrix = new Array(nodes.length)
.fill()
.map(() => new Array(nodes.length).fill(null))
// Формируем матрицу.
// Перебираем узлы
nodes.forEach((node, index) => {
// Перебираем соседей узла
node.getNeighbors().forEach((neighbor) => {
// Индекс соседа
const neighborIndex = indices[neighbor.getKey()]
// [индекс узла][индекс соседа] = вес ребра
matrix[index][neighborIndex] = this.findEdge(node, neighbor).weight
})
})
return matrix
}
// Возвращает строковое представление графа
toString() {
return Object.keys(this.nodes).toString()
}
}
Проверяем, что код графа работает, как ожидается
// data-structures/graph/__tests__/graph.test.js
import Graph from '..'
import Node from '../node'
import Edge from '../edge'
describe('Graph', () => {
it('должен добавить узлы в граф', () => {
const graph = new Graph()
const nodeA = new Node('A')
const nodeB = new Node('B')
graph.addNode(nodeA).addNode(nodeB)
expect(graph.toString()).toBe('A,B')
expect(graph.getNodeByKey(nodeA.getKey())).toEqual(nodeA)
expect(graph.getNodeByKey(nodeB.getKey())).toEqual(nodeB)
})
it('должен добавить ребра в ненаправленный граф', () => {
const graph = new Graph()
const nodeA = new Node('A')
const nodeB = new Node('B')
const edgeAB = new Edge(nodeA, nodeB)
graph.addEdge(edgeAB)
expect(graph.getAllNodes().length).toBe(2)
expect(graph.getAllNodes()[0]).toEqual(nodeA)
expect(graph.getAllNodes()[1]).toEqual(nodeB)
const graphNodeA = graph.getNodeByKey(nodeA.getKey())
const graphNodeB = graph.getNodeByKey(nodeB.getKey())
expect(graph.toString()).toBe('A,B')
expect(graphNodeA).toBeDefined()
expect(graphNodeB).toBeDefined()
expect(graph.getNodeByKey('not existing')).toBeUndefined()
expect(graphNodeA.getNeighbors().length).toBe(1)
expect(graphNodeA.getNeighbors()[0]).toEqual(nodeB)
expect(graphNodeA.getNeighbors()[0]).toEqual(graphNodeB)
expect(graphNodeB.getNeighbors().length).toBe(1)
expect(graphNodeB.getNeighbors()[0]).toEqual(nodeA)
expect(graphNodeB.getNeighbors()[0]).toEqual(graphNodeA)
})
it('должен добавить ребра в направленный граф', () => {
const graph = new Graph(true)
const nodeA = new Node('A')
const nodeB = new Node('B')
const edgeAB = new Edge(nodeA, nodeB)
graph.addEdge(edgeAB)
const graphNodeA = graph.getNodeByKey(nodeA.getKey())
const graphNodeB = graph.getNodeByKey(nodeB.getKey())
expect(graph.toString()).toBe('A,B')
expect(graphNodeA).toBeDefined()
expect(graphNodeB).toBeDefined()
expect(graphNodeA.getNeighbors().length).toBe(1)
expect(graphNodeA.getNeighbors()[0]).toEqual(nodeB)
expect(graphNodeA.getNeighbors()[0]).toEqual(graphNodeB)
expect(graphNodeB.getNeighbors().length).toBe(0)
})
it('должен найти ребра по узлам в ненаправленном графе', () => {
const graph = new Graph()
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeAB = new Edge(nodeA, nodeB, 10)
graph.addEdge(edgeAB)
const graphEdgeAB = graph.findEdge(nodeA, nodeB)
const graphEdgeBA = graph.findEdge(nodeB, nodeA)
const graphEdgeAC = graph.findEdge(nodeA, nodeC)
const graphEdgeCA = graph.findEdge(nodeC, nodeA)
expect(graphEdgeAC).toBeNull()
expect(graphEdgeCA).toBeNull()
expect(graphEdgeAB).toEqual(edgeAB)
expect(graphEdgeBA).toEqual(edgeAB)
expect(graphEdgeAB.weight).toBe(10)
})
it('должен найти ребра по узлам в направленном графе', () => {
const graph = new Graph(true)
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeAB = new Edge(nodeA, nodeB, 10)
graph.addEdge(edgeAB)
const graphEdgeAB = graph.findEdge(nodeA, nodeB)
const graphEdgeBA = graph.findEdge(nodeB, nodeA)
const graphEdgeAC = graph.findEdge(nodeA, nodeC)
const graphEdgeCA = graph.findEdge(nodeC, nodeA)
expect(graphEdgeAC).toBeNull()
expect(graphEdgeCA).toBeNull()
expect(graphEdgeBA).toBeNull()
expect(graphEdgeAB).toEqual(edgeAB)
expect(graphEdgeAB.weight).toBe(10)
})
it('должен вернуть соседей узла', () => {
const graph = new Graph(true)
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeAB = new Edge(nodeA, nodeB)
const edgeAC = new Edge(nodeA, nodeC)
graph.addEdge(edgeAB).addEdge(edgeAC)
const neighbors = graph.getNeighbors(nodeA)
expect(neighbors.length).toBe(2)
expect(neighbors[0]).toEqual(nodeB)
expect(neighbors[1]).toEqual(nodeC)
})
it('должен выбросить исключение при повторном добавлении ребра', () => {
function addSameEdgeTwice() {
const graph = new Graph(true)
const nodeA = new Node('A')
const nodeB = new Node('B')
const edgeAB = new Edge(nodeA, nodeB)
graph.addEdge(edgeAB).addEdge(edgeAB)
}
expect(addSameEdgeTwice).toThrow()
})
it('должен вернуть список всех добавленных узлов', () => {
const graph = new Graph(true)
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeAB = new Edge(nodeA, nodeB)
const edgeBC = new Edge(nodeB, nodeC)
graph.addEdge(edgeAB).addEdge(edgeBC)
const edges = graph.getAllEdges()
expect(edges.length).toBe(2)
expect(edges[0]).toEqual(edgeAB)
expect(edges[1]).toEqual(edgeBC)
})
it('должен вычислить общий вес дефолтного графа', () => {
const graph = new Graph()
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const nodeD = new Node('D')
const edgeAB = new Edge(nodeA, nodeB)
const edgeBC = new Edge(nodeB, nodeC)
const edgeCD = new Edge(nodeC, nodeD)
const edgeAD = new Edge(nodeA, nodeD)
graph.addEdge(edgeAB).addEdge(edgeBC).addEdge(edgeCD).addEdge(edgeAD)
expect(graph.getWeight()).toBe(0)
})
it('должен вычислить общий вес взвешенного графа', () => {
const graph = new Graph()
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const nodeD = new Node('D')
const edgeAB = new Edge(nodeA, nodeB, 1)
const edgeBC = new Edge(nodeB, nodeC, 2)
const edgeCD = new Edge(nodeC, nodeD, 3)
const edgeAD = new Edge(nodeA, nodeD, 4)
graph.addEdge(edgeAB).addEdge(edgeBC).addEdge(edgeCD).addEdge(edgeAD)
expect(graph.getWeight()).toBe(10)
})
it('должен удалить ребра из графа', () => {
const graph = new Graph()
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeAB = new Edge(nodeA, nodeB)
const edgeBC = new Edge(nodeB, nodeC)
const edgeAC = new Edge(nodeA, nodeC)
graph.addEdge(edgeAB).addEdge(edgeBC).addEdge(edgeAC)
expect(graph.getAllEdges().length).toBe(3)
graph.removeEdge(edgeAB)
expect(graph.getAllEdges().length).toBe(2)
expect(graph.getAllEdges()[0].getKey()).toBe(edgeBC.getKey())
expect(graph.getAllEdges()[1].getKey()).toBe(edgeAC.getKey())
})
it('должен выбросить исключение при удалении несуществующего узла', () => {
function deleteNotExistingEdge() {
const graph = new Graph()
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const edgeAB = new Edge(nodeA, nodeB)
const edgeBC = new Edge(nodeB, nodeC)
graph.addEdge(edgeAB)
graph.removeEdge(edgeBC)
}
expect(deleteNotExistingEdge).toThrowError()
})
it('должен инвертировать граф', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const nodeD = new Node('D')
const edgeAB = new Edge(nodeA, nodeB)
const edgeAC = new Edge(nodeA, nodeC)
const edgeCD = new Edge(nodeC, nodeD)
const graph = new Graph(true)
graph.addEdge(edgeAB).addEdge(edgeAC).addEdge(edgeCD)
expect(graph.toString()).toBe('A,B,C,D')
expect(graph.getAllEdges().length).toBe(3)
expect(graph.getNeighbors(nodeA).length).toBe(2)
expect(graph.getNeighbors(nodeA)[0].getKey()).toBe(nodeB.getKey())
expect(graph.getNeighbors(nodeA)[1].getKey()).toBe(nodeC.getKey())
expect(graph.getNeighbors(nodeB).length).toBe(0)
expect(graph.getNeighbors(nodeC).length).toBe(1)
expect(graph.getNeighbors(nodeC)[0].getKey()).toBe(nodeD.getKey())
expect(graph.getNeighbors(nodeD).length).toBe(0)
graph.reverse()
expect(graph.toString()).toBe('A,B,C,D')
expect(graph.getAllEdges().length).toBe(3)
expect(graph.getNeighbors(nodeA).length).toBe(0)
expect(graph.getNeighbors(nodeB).length).toBe(1)
expect(graph.getNeighbors(nodeB)[0].getKey()).toBe(nodeA.getKey())
expect(graph.getNeighbors(nodeC).length).toBe(1)
expect(graph.getNeighbors(nodeC)[0].getKey()).toBe(nodeA.getKey())
expect(graph.getNeighbors(nodeD).length).toBe(1)
expect(graph.getNeighbors(nodeD)[0].getKey()).toBe(nodeC.getKey())
})
it('должен вернуть индексы узлов', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const nodeD = new Node('D')
const edgeAB = new Edge(nodeA, nodeB)
const edgeBC = new Edge(nodeB, nodeC)
const edgeCD = new Edge(nodeC, nodeD)
const edgeBD = new Edge(nodeB, nodeD)
const graph = new Graph()
graph.addEdge(edgeAB).addEdge(edgeBC).addEdge(edgeCD).addEdge(edgeBD)
const verticesIndices = graph.getNodesIndices()
expect(verticesIndices).toEqual({
A: 0,
B: 1,
C: 2,
D: 3,
})
})
it('должен вернуть матрицу смежности для ненаправленного графа', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const nodeD = new Node('D')
const edgeAB = new Edge(nodeA, nodeB)
const edgeBC = new Edge(nodeB, nodeC)
const edgeCD = new Edge(nodeC, nodeD)
const edgeBD = new Edge(nodeB, nodeD)
const graph = new Graph()
graph.addEdge(edgeAB).addEdge(edgeBC).addEdge(edgeCD).addEdge(edgeBD)
const adjacencyMatrix = graph.getAdjacencyMatrix()
expect(adjacencyMatrix).toEqual([
[null, 0, null, null],
[0, null, 0, 0],
[null, 0, null, 0],
[null, 0, 0, null],
])
})
it('должен вернуть матрицу смежности для направленного графа', () => {
const nodeA = new Node('A')
const nodeB = new Node('B')
const nodeC = new Node('C')
const nodeD = new Node('D')
const edgeAB = new Edge(nodeA, nodeB, 2)
const edgeBC = new Edge(nodeB, nodeC, 1)
const edgeCD = new Edge(nodeC, nodeD, 5)
const edgeBD = new Edge(nodeB, nodeD, 7)
const graph = new Graph(true)
graph.addEdge(edgeAB).addEdge(edgeBC).addEdge(edgeCD).addEdge(edgeBD)
const adjacencyMatrix = graph.getAdjacencyMatrix()
expect(adjacencyMatrix).toEqual([
[null, 2, null, null],
[null, null, 1, 7],
[null, null, null, 5],
[null, null, null, null],
])
})
})
Запускаем тесты:
npm run test ./data-structures/graph/__tests__/graph
Результат:

Система непересекающихся множеств
Описание
Система непересекающихся множеств (disjoint set) (также называемая структурой данных поиска объединения (пересечения) (union-find data structure) или множеством поиска слияния (merge-find set)) - это структура данных, которая содержит множество элементов, разделенных на определенное количество непересекающихся подмножеств. Она обеспечивает почти константное время выполнения операций (ограниченное обратной функцией Аккермана) добавления новых множеств, объединения существующих множеств и определения принадлежности элементов к одному множеству. Среди прочего, СНМ играет ключевую роль в алгоритме Краскала для построения минимального остовного дерева взвешенного связного неориентированного графа.
Основные операции СНМ:
MakeSet(x)- создает одноэлементное множество{x}Find(x)- возвращает идентификатор множества (выделенный или репрезентативный элемент), содержащего элементxUnion(x, y)- объединяет множества, содержащиеxиy

8 непересекающихся множеств, созданных с помощью MakeSet

Группировка множеств с помощью Union
Реализация
Начнем с реализации конструктора выделенного элемента множества:
// data-structures/disjoin-set/item.js
export default class Item {
constructor(value, keyCb) {
// Значение
this.value = value
// Кастомная функция извлечения ключа
this.keyCb = keyCb
// Родительский узел
this.parent = null
// Дочерние узлы
this.children = {}
}
}
Методы получения значения узла, корневого узла и определения того, является ли узел корневым:
// Возвращает ключ (значение)
getKey() {
if (this.keyCb) {
return this.keyCb(this.value)
}
return this.value
}
// Возвращает корневой узел
getRoot() {
return this.isRoot() ? this : this.parent.getRoot()
}
// Определяет, является ли узел корневым
isRoot() {
return this.parent === null
}
Методы получения ранга и потомков узла:
// Возвращает ранг (вес) узла
getRank() {
const children = this.getChildren()
if (children.length === 0) {
return 0
}
let rank = 0
for (const child of children) {
rank += 1
rank += child.getRank()
}
return rank
}
// Возвращает потомков
getChildren() {
return Object.values(this.children)
}
Методы установки родительского и добавления дочернего узла:
// Устанавливает предка
setParent(parent, forceSettingParentChild = true) {
this.parent = parent
if (forceSettingParentChild) {
parent.addChild(this)
}
return this
}
// Добавляет потомка
addChild(child) {
this.children[child.getKey()] = child
child.setParent(this, false)
return this
}
Полный код узла
export default class Item {
constructor(value, keyCb) {
// Значение
this.value = value
// Кастомная функция извлечения ключа
this.keyCb = keyCb
// Родительский узел
this.parent = null
// Дочерние узлы
this.children = {}
}
// Возвращает ключ (значение)
getKey() {
if (this.keyCb) {
return this.keyCb(this.value)
}
return this.value
}
// Возвращает корневой узел
getRoot() {
return this.isRoot() ? this : this.parent.getRoot()
}
// Определяет, является ли узел корневым
isRoot() {
return this.parent === null
}
// Возвращает ранг (вес) узла
getRank() {
const children = this.getChildren()
if (children.length === 0) {
return 0
}
let rank = 0
for (const child of children) {
rank += 1
rank += child.getRank()
}
return rank
}
// Возвращает потомков
getChildren() {
return Object.values(this.children)
}
// Устанавливает предка
setParent(parent, forceSettingParentChild = true) {
this.parent = parent
if (forceSettingParentChild) {
parent.addChild(this)
}
return this
}
// Добавляет потомка
addChild(child) {
this.children[child.getKey()] = child
child.setParent(this, false)
return this
}
}
Приступаем к реализации СНМ:
// data-structures/disjoin-set/index.js
import Item from './item'
export default class DisjointSet {
constructor(cb) {
// Кастомная функция извлечения ключа (значения) узла
this.cb = cb
// Непересекающиеся подмножества
this.items = {}
}
}
Метод создания подмножества:
// Создает подмножество
makeSet(value) {
// Создаем выделенный элемент
const item = new Item(value, this.cb)
// Добавляем подмножество в список
if (!this.items[item.getKey()]) {
this.items[item.getKey()] = item
}
return this
}
Метод по�иска выделенного элемента:
// Ищет выделенный элемент
find(value) {
const temp = new Item(value, this.cb)
const item = this.items[temp.getKey()]
return item ? item.getRoot().getKey() : null
}
Метод объединения двух подмножеств:
// Объединяет подмножества
union(value1, value2) {
const root1 = this.find(value1)
const root2 = this.find(value2)
if (!root1 || !root2) {
throw new Error('Одно или оба значения отсутствуют!')
}
if (root1 === root2) {
return this
}
const item1 = this.items[root1]
const item2 = this.items[root2]
// Определяем, какое подмножество имеет больший ранг.
// Подмножество с меньшим рангом становится потомком подмножества с большим рангом
if (item1.getRank() < item2.getRank()) {
item2.addChild(item1)
return this
}
item1.addChild(item2)
return this
}
Метод определения принадлежности двух элементов к одному множеству:
// Определяет, принадлежат ли значения к одному множеству
isSameSet(value1, value2) {
const root1 = this.find(value1)
const root2 = this.find(value2)
if (!root1 || !root2) {
throw new Error('Одно или оба значения отсутствуют!')
}
return root1 === root2
}
Полный код СНМ
import Item from './item'
export default class DisjointSet {
constructor(cb) {
// Кастомная функция извлечения ключа (значения) узла
this.cb = cb
// Непересекающиеся подмножества
this.items = {}
}
// Создает подмножество
makeSet(value) {
// Создаем выделенный элемент
const item = new Item(value, this.cb)
// Добавляем подмножество в список
if (!this.items[item.getKey()]) {
this.items[item.getKey()] = item
}
return this
}
// Ищет выделенный элемент
find(value) {
const temp = new Item(value, this.cb)
const item = this.items[temp.getKey()]
return item ? item.getRoot().getKey() : null
}
// Объединяет подмножества
union(value1, value2) {
const root1 = this.find(value1)
const root2 = this.find(value2)
if (!root1 || !root2) {
throw new Error('Одно или оба значения отсутствуют!')
}
if (root1 === root2) {
return this
}
const item1 = this.items[root1]
const item2 = this.items[root2]
// Определяем, какое подмножество имеет больший ранг.
// Подмножество с меньшим рангом становится потомком подмножества с большим рангом
if (item1.getRank() < item2.getRank()) {
item2.addChild(item1)
return this
}
item1.addChild(item2)
return this
}
// Определяет, принадлежат ли значения к одному множеству
isSameSet(value1, value2) {
const root1 = this.find(value1)
const root2 = this.find(value2)
if (!root1 || !root2) {
throw new Error('Одно или оба значения отсутствуют!')
}
return root1 === root2
}
}
Автономную СНМ (без дополнительных зависимостей) можно реализовать следующим образом:
export default class DisjointSetAdHoc {
constructor(size) {
this.roots = new Array(size).fill(0).map((_, i) => i)
this.heights = new Array(size).fill(1)
}
find(a) {
if (this.roots[a] === a) return a
this.roots[a] = this.find(this.roots[a])
return this.roots[a]
}
union(a, b) {
const rootA = this.find(a)
const rootB = this.find(b)
if (rootA === rootB) return
if (this.heights[rootA] < this.heights[rootB]) {
this.roots[rootA] = rootB
} else if (this.heights[rootA] > this.heights[rootB]) {
this.roots[rootB] = rootA
} else {
this.roots[rootB] = rootA
this.heights[rootA]++
}
}
connected(a, b) {
return this.find(a) === this.find(b)
}
}
Тестирование
Проверяем, что код выделенного элемента работает, как ожидается
// data-structures/disjoint-set/__tests__/item.test.js
import Item from '../item'
describe('Item', () => {
it('должен выполнить базовые манипуляции с выделенным элементом', () => {
const itemA = new Item('A')
const itemB = new Item('B')
const itemC = new Item('C')
const itemD = new Item('D')
expect(itemA.getRank()).toBe(0)
expect(itemA.getChildren()).toEqual([])
expect(itemA.getKey()).toBe('A')
expect(itemA.getRoot()).toEqual(itemA)
expect(itemA.isRoot()).toBe(true)
expect(itemB.isRoot()).toBe(true)
itemA.addChild(itemB)
itemD.setParent(itemC)
expect(itemA.getRank()).toBe(1)
expect(itemC.getRank()).toBe(1)
expect(itemB.getRank()).toBe(0)
expect(itemD.getRank()).toBe(0)
expect(itemA.getChildren().length).toBe(1)
expect(itemC.getChildren().length).toBe(1)
expect(itemA.getChildren()[0]).toEqual(itemB)
expect(itemC.getChildren()[0]).toEqual(itemD)
expect(itemB.getChildren().length).toBe(0)
expect(itemD.getChildren().length).toBe(0)
expect(itemA.getRoot()).toEqual(itemA)
expect(itemB.getRoot()).toEqual(itemA)
expect(itemC.getRoot()).toEqual(itemC)
expect(itemD.getRoot()).toEqual(itemC)
expect(itemA.isRoot()).toBe(true)
expect(itemB.isRoot()).toBe(false)
expect(itemC.isRoot()).toBe(true)
expect(itemD.isRoot()).toBe(false)
itemA.addChild(itemC)
expect(itemA.isRoot()).toBe(true)
expect(itemB.isRoot()).toBe(false)
expect(itemC.isRoot()).toBe(false)
expect(itemD.isRoot()).toBe(false)
expect(itemA.getRank()).toEqual(3)
expect(itemB.getRank()).toEqual(0)
expect(itemC.getRank()).toEqual(1)
})
it('должен выполнить базовые манипуляции с выделенным элементом с кастомной функцией извлечения ключа', () => {
const keyExtractor = (value) => value.key
const itemA = new Item({ key: 'A', value: 1 }, keyExtractor)
const itemB = new Item({ key: 'B', value: 2 }, keyExtractor)
const itemC = new Item({ key: 'C', value: 3 }, keyExtractor)
const itemD = new Item({ key: 'D', value: 4 }, keyExtractor)
expect(itemA.getRank()).toBe(0)
expect(itemA.getChildren()).toEqual([])
expect(itemA.getKey()).toBe('A')
expect(itemA.getRoot()).toEqual(itemA)
expect(itemA.isRoot()).toBe(true)
expect(itemB.isRoot()).toBe(true)
itemA.addChild(itemB)
itemD.setParent(itemC)
expect(itemA.getRank()).toBe(1)
expect(itemC.getRank()).toBe(1)
expect(itemB.getRank()).toBe(0)
expect(itemD.getRank()).toBe(0)
expect(itemA.getChildren().length).toBe(1)
expect(itemC.getChildren().length).toBe(1)
expect(itemA.getChildren()[0]).toEqual(itemB)
expect(itemC.getChildren()[0]).toEqual(itemD)
expect(itemB.getChildren().length).toBe(0)
expect(itemD.getChildren().length).toBe(0)
expect(itemA.getRoot()).toEqual(itemA)
expect(itemB.getRoot()).toEqual(itemA)
expect(itemC.getRoot()).toEqual(itemC)
expect(itemD.getRoot()).toEqual(itemC)
expect(itemA.isRoot()).toBe(true)
expect(itemB.isRoot()).toBe(false)
expect(itemC.isRoot()).toBe(true)
expect(itemD.isRoot()).toBe(false)
itemA.addChild(itemC)
expect(itemA.isRoot()).toBe(true)
expect(itemB.isRoot()).toBe(false)
expect(itemC.isRoot()).toBe(false)
expect(itemD.isRoot()).toBe(false)
expect(itemA.getRank()).toEqual(3)
expect(itemB.getRank()).toEqual(0)
expect(itemC.getRank()).toEqual(1)
})
})
Выполняем тесты:
npm run test ./data-structures/disjoint-set/__tests__/item
Результаты:

Проверяем, что код СНМ работает, как ожидается
// data-structures/disjoint-set/__tests__/disjoint-set.test.js
import DisjointSet from '..'
describe('DisjointSet', () => {
it('должен выбросить исключения при объединении и проверке несуществующих множеств', () => {
function mergeNotExistingSets() {
const disjointSet = new DisjointSet()
disjointSet.union('A', 'B')
}
function checkNotExistingSets() {
const disjointSet = new DisjointSet()
disjointSet.isSameSet('A', 'B')
}
expect(mergeNotExistingSets).toThrow()
expect(checkNotExistingSets).toThrow()
})
it('должен выполнить базовые манипуляции с системой непересекающихся множеств', () => {
const disjointSet = new DisjointSet()
expect(disjointSet.find('A')).toBeNull()
expect(disjointSet.find('B')).toBeNull()
disjointSet.makeSet('A')
expect(disjointSet.find('A')).toBe('A')
expect(disjointSet.find('B')).toBeNull()
disjointSet.makeSet('B')
expect(disjointSet.find('A')).toBe('A')
expect(disjointSet.find('B')).toBe('B')
disjointSet.makeSet('C')
expect(disjointSet.isSameSet('A', 'B')).toBe(false)
disjointSet.union('A', 'B')
expect(disjointSet.find('A')).toBe('A')
expect(disjointSet.find('B')).toBe('A')
expect(disjointSet.isSameSet('A', 'B')).toBe(true)
expect(disjointSet.isSameSet('B', 'A')).toBe(true)
expect(disjointSet.isSameSet('A', 'C')).toBe(false)
disjointSet.union('A', 'A')
disjointSet.union('B', 'C')
expect(disjointSet.find('A')).toBe('A')
expect(disjointSet.find('B')).toBe('A')
expect(disjointSet.find('C')).toBe('A')
expect(disjointSet.isSameSet('A', 'B')).toBe(true)
expect(disjointSet.isSameSet('B', 'C')).toBe(true)
expect(disjointSet.isSameSet('A', 'C')).toBe(true)
disjointSet.makeSet('E').makeSet('F').makeSet('G').makeSet('H').makeSet('I')
disjointSet.union('E', 'F').union('F', 'G').union('G', 'H').union('H', 'I')
expect(disjointSet.isSameSet('A', 'I')).toBe(false)
expect(disjointSet.isSameSet('E', 'I')).toBe(true)
disjointSet.union('I', 'C')
expect(disjointSet.find('I')).toBe('E')
expect(disjointSet.isSameSet('A', 'I')).toBe(true)
})
it('должен выполнить базовые манипуляции с системой непересекающихся множеств с кастомной функцией извлечения ключа', () => {
const keyExtractor = (value) => value.key
const disjointSet = new DisjointSet(keyExtractor)
const itemA = { key: 'A', value: 1 }
const itemB = { key: 'B', value: 2 }
const itemC = { key: 'C', value: 3 }
expect(disjointSet.find(itemA)).toBeNull()
expect(disjointSet.find(itemB)).toBeNull()
disjointSet.makeSet(itemA)
expect(disjointSet.find(itemA)).toBe('A')
expect(disjointSet.find(itemB)).toBeNull()
disjointSet.makeSet(itemB)
expect(disjointSet.find(itemA)).toBe('A')
expect(disjointSet.find(itemB)).toBe('B')
disjointSet.makeSet(itemC)
expect(disjointSet.isSameSet(itemA, itemB)).toBe(false)
disjointSet.union(itemA, itemB)
expect(disjointSet.find(itemA)).toBe('A')
expect(disjointSet.find(itemB)).toBe('A')
expect(disjointSet.isSameSet(itemA, itemB)).toBe(true)
expect(disjointSet.isSameSet(itemB, itemA)).toBe(true)
expect(disjointSet.isSameSet(itemA, itemC)).toBe(false)
disjointSet.union(itemA, itemC)
expect(disjointSet.find(itemA)).toBe('A')
expect(disjointSet.find(itemB)).toBe('A')
expect(disjointSet.find(itemC)).toBe('A')
expect(disjointSet.isSameSet(itemA, itemB)).toBe(true)
expect(disjointSet.isSameSet(itemB, itemC)).toBe(true)
expect(disjointSet.isSameSet(itemA, itemC)).toBe(true)
})
it('должен объединить меньшее множество с большим, сделав большее новым выделенным элементом', () => {
const disjointSet = new DisjointSet()
disjointSet
.makeSet('A')
.makeSet('B')
.makeSet('C')
.union('B', 'C')
.union('A', 'C')
expect(disjointSet.find('A')).toBe('B')
})
})
Выполняем тесты:
npm run test ./data-structures/disjoint-set/__tests__/disjoint-set
Результаты:

Проверяем, что код автономного СНМ работает, как ожидается
// data-structures/disjoint-set/__tests__/ad-hoc.test.js
import DisjointSetAdhoc from '../ad-hoc'
describe('DisjointSetAdhoc', () => {
it('должен создать множества и найти соединенные элементы', () => {
const set = new DisjointSetAdhoc(10)
// 1-2-5-6-7 3-8-9 4
set.union(1, 2)
set.union(2, 5)
set.union(5, 6)
set.union(6, 7)
set.union(3, 8)
set.union(8, 9)
expect(set.connected(1, 5)).toBe(true)
expect(set.connected(5, 7)).toBe(true)
expect(set.connected(3, 8)).toBe(true)
expect(set.connected(4, 9)).toBe(false)
expect(set.connected(4, 7)).toBe(false)
// 1-2-5-6-7 3-8-9-4
set.union(9, 4)
expect(set.connected(4, 9)).toBe(true)
expect(set.connected(4, 3)).toBe(true)
expect(set.connected(8, 4)).toBe(true)
expect(set.connected(8, 7)).toBe(false)
expect(set.connected(2, 3)).toBe(false)
})
it('должен сохранять высоту дерева маленькой', () => {
const set = new DisjointSetAdhoc(10)
// 1-2-6-7-9 1 3 4 5
set.union(7, 6)
set.union(1, 2)
set.union(2, 6)
set.union(1, 7)
set.union(9, 1)
expect(set.connected(1, 7)).toBe(true)
expect(set.connected(6, 9)).toBe(true)
expect(set.connected(4, 9)).toBe(false)
expect(Math.max(...set.heights)).toBe(3)
})
})
Выполняем тесты:
npm run test ./data-structures/disjoint-set/__tests__/ad-hoc
Результаты:

Фильтр Блума
Описание
Фильтр Блума (Bloom filter) - это пространственно-эффективная вероятностная структура данных, предназначенная для определения наличия элемента во множестве. С одной стороны, эта структура является очень быстрой и использует минимальный объем памяти, с другой стороны, возможны ложноположительные (false positive) результаты. Ложноотрицательные (false negative) результаты невозможны. Другими словами, фильтр возвращает либо "элемент МОЖЕТ содержаться во множестве", либо "элемент ТОЧНО НЕ содержится во множестве". Фильтр Блума может использовать любое количество памяти, но, как правило, чем больше памяти, тем ниже вероятность ложноположительных результатов.
Блум предложил эту технику для применения в областях, где количество исходных данных потребовало бы непрактично много памяти в случае применения условно безошибочных техник хеширования.
Описание алгоритма
Пустой фильтр Блума представлен ма�ссивом из m битов, установленных в 0. Должно быть определено k независимых хеш-функций, отображающих каждый элемент множества в одну из m позиций массива, генерируя единообразное случайное распределение. Обычно k задается константой, которая намного меньше m и пропорциональна количеству добавляемых элементов. Точный выбор k и постоянной пропорциональности m определяются уровнем ложных срабатываний фильтра.
Вот пример фильтра Блума, представляющего множество {x, y, z}. Цветные стрелки показывают позиции (индексы) битового массива, соответствующие элементам множества. Элемент w не содержится во множестве {x, y, z}, потому что он привязан к позиции массива, равной 0. В данном случае m = 18, а k = 3.
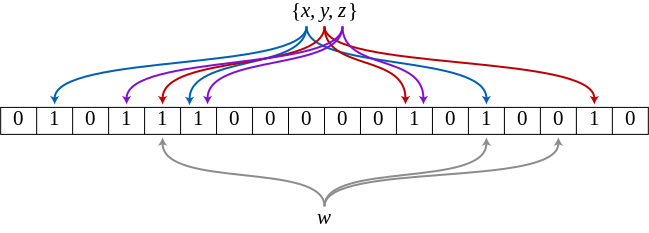
Для добавления в фильтр элемента e необходимо записать 1 в каждую позицию h1(e), ..., hk(e) (хеш-функции) битового массива.
Для определения наличия элемента e во множестве необходимо проверить состояние битов h1(e), ..., hk(e). Если хот�я бы один бит имеет значение 0, элемент отсутствует. Если все биты имеют значение 1, структура сообщает, что элемент присутствует. При этом, может возникнуть две ситуации: либо элемент действительно содержится во множестве, либо все биты оказались установлены случайно при добавлении других элементов. Второй случай является источником ложноположительных результатов.
Операции
Фильтр Блума позволяет выполнять две основные операции: вставка и поиск элемента. Поиск может завершаться ложноположительными результатами. Удаление элементов возможно, но проблематично.
Другими словами, в фильтр можно добавлять элементы, а на вопрос о наличии элемента структура отвечает либо "нет", либо "возможно".
Операции вставки и поиска выполняются за время O(1).
Создание фильтра
При создании фильтра указывается его размер. Размер нашего фильтра составляет 100. Все элементы устанавливаются в false (по сути, тоже самое, что 0).
В процессе добавления генерируется хеш элемента с помощью трех хеш-функций. Эти функции возвращают индексы. Значение по каждому индексу обновляется на true.
В процессе поиска также генерируется хеш элемента. Затем проверяется, что все значения по индексам являются true. Если это так, то элемент может содержаться во множестве.
Однако мы не можем быть в этом уверены на 100%, поскольку биты могли быть установлены при добавлении других элементов.
Если хотя бы одно значение равняется false, элемент точно отсутствует во множестве.
Ложноположительные результаты
Вероятность ложноположительных срабатываний определяется тремя факторами: размером фильтра (m), количеством используемых хеш-функций (k) и количеством элементов, добавляемых в фильтр (n).
Формула выглядит следующим образом:
( 1 - e -kn/m ) k
Значения этих переменных выбираются, исходя из приемлемости ложноположительных результатов.
Применение
Фильтр Блума может использоваться в блогах. Он идеально подходит для определения статей, которые пользователь еще не читал, за счет добавления в фильтр статей, прочитанных им.
Некоторые статьи будут отфильтрованы по ошибке, но цена приемлема: пользователь не увидит нескольких статей, зато ему будут показываться новые статьи при каждом посещении сайта.
Подробнее о фильтре Блума можно почитать в этой статье.
Реализация
Приступаем к реализации фильтра Блума:
// data-structures/bloom-filter.js
export default class BloomFilter {
// Размер фильтра напрямую влияет на вероятность ложноположительных результат�ов.
// Как правило, чем больше размер, тем такая вероятность ниже
constructor(size = 100) {
// Размер фильтра
this.size = size
// Хранилище (по сути, сам фильтр)
this.storage = this.createStore(size)
}
}
Метод добавления элемента в фильтр:
// Добавляет элемент в фильтр
insert(item) {
// Вычисляем хеш элемента (индексы массива в количестве 3 штук)
const hashValues = this.getHashValues(item)
// Устанавливаем значение по каждому индексу в `true`
hashValues.forEach((v) => this.storage.setValue(v))
}
Метод определения наличия элемента в фильтре:
// Определяет наличие элемента в фильтре
mayContain(item) {
// Вычисляем хеш элемента
const hashValues = this.getHashValues(item)
// Перебираем индексы
for (const v of hashValues) {
// Если хотя бы одно значение равняется `false`
if (!this.storage.getValue(v)) {
// Элемент точно отсутствует
return false
}
}
// Элемент может присутствовать
return true
}
Метод создания хранилища (по сути, фильтра):
// Создает хранилище
createStore(size) {
// Хранилище - массив указанного размера, заполненный `false`
const storage = new Array(size).fill(false)
// Возвращается объект с "геттером" и "сеттером"
return {
getValue(i) {
return storage[i]
},
setValue(i) {
storage[i] = true
},
}
}
Хеш-функции (довольно примитивные, надо сказать):
// Хеш-функции
hash1(item) {
let hash = 0
for (let i = 0; i < item.length; i++) {
const char = item.charCodeAt(i)
hash = (hash << 5) + hash + char
hash &= hash // конвертируем значение в 32-битное целое число
hash = Math.abs(hash)
}
return hash % this.size
}
hash2(item) {
let hash = 5381
for (let i = 0; i < item.length; i++) {
const char = item.charCodeAt(i)
hash = (hash << 5) + hash + char // hash * 33 + char
}
return Math.abs(hash % this.size)
}
hash3(item) {
let hash = 0
for (let i = 0; i < item.length; i++) {
const char = item.charCodeAt(i)
hash = (hash << 5) - hash + char
hash &= hash // конвертируем значение в 32-битное целое число
}
return Math.abs(hash % this.size)
}
Наконец, метод генерации хеша:
// Генерирует хеш элемента.
// Возвращает массив из трех индексов
getHashValues(item) {
return [this.hash1(item), this.hash2(item), this.hash3(item)]
}
Полный код фильтра Блума
export default class BloomFilter {
// Размер фильтра напрямую влияет на вероятность ложноположительных результатов.
// Как правило, чем больше размер, тем такая вероятность ниже
constructor(size = 100) {
// Размер фильтра
this.size = size
// Хранилище (по сути, сам фильтр)
this.storage = this.createStore(size)
}
// Добавляет элемент в фильтр
insert(item) {
// Вычисляем хеш элемента (индексы массива в количестве 3 штук)
const hashValues = this.getHashValues(item)
// Устанавливаем значение по каждому индексу в `true`
hashValues.forEach((v) => this.storage.setValue(v))
}
// Определяет наличие элемента в фильтре
mayContain(item) {
// Вычисляем хеш элемента
const hashValues = this.getHashValues(item)
// Перебираем индексы
for (const v of hashValues) {
// Если хотя бы одно значение равняется `false`
if (!this.storage.getValue(v)) {
// Элемент точно отсутствует
return false
}
}
// Элемент может присутствовать
return true
}
// Создает хранилище
createStore(size) {
// Хранилище - массив указанного размера, заполненный `false`
const storage = new Array(size).fill(false)
// Возвращается объект с "геттером" и "сеттером"
return {
getValue(i) {
return storage[i]
},
setValue(i) {
storage[i] = true
},
}
}
// Хеш-функции
hash1(item) {
let hash = 0
for (let i = 0; i < item.length; i++) {
const char = item.charCodeAt(i)
hash = (hash << 5) + hash + char
hash &= hash // конвертируем значение в 32-битное целое число
hash = Math.abs(hash)
}
return hash % this.size
}
hash2(item) {
let hash = 5381
for (let i = 0; i < item.length; i++) {
const char = item.charCodeAt(i)
hash = (hash << 5) + hash + char // hash * 33 + char
}
return Math.abs(hash % this.size)
}
hash3(item) {
let hash = 0
for (let i = 0; i < item.length; i++) {
const char = item.charCodeAt(i)
hash = (hash << 5) - hash + char
hash &= hash // конвертируем значение в 32-битное целое число
}
return Math.abs(hash % this.size)
}
// Генерирует хеш элемента.
// Возвращает массив из трех индексов
getHashValues(item) {
return [this.hash1(item), this.hash2(item), this.hash3(item)]
}
}
Тестирование
Проверяем, что код фильтра работает, как ожидается
// data-structures/__tests__/bloom-filter.test.js
import BloomFilter from '../bloom-filter'
describe('BloomFilter', () => {
let bloomFilter
const people = ['Bruce Wayne', 'Clark Kent', 'Barry Allen']
beforeEach(() => {
bloomFilter = new BloomFilter()
})
it('должен содержать методы "insert" и "mayContain"', () => {
expect(typeof bloomFilter.insert).toBe('function')
expect(typeof bloomFilter.mayContain).toBe('function')
})
it('должен создать хранилище с указанными методами', () => {
const store = bloomFilter.createStore(18)
expect(typeof store.getValue).toBe('function')
expect(typeof store.setValue).toBe('function')
})
it('должен стабильно хешировать элементы с помощью трех хеш-функций', () => {
const str1 = 'apple'
expect(bloomFilter.hash1(str1)).toEqual(bloomFilter.hash1(str1))
expect(bloomFilter.hash2(str1)).toEqual(bloomFilter.hash2(str1))
expect(bloomFilter.hash3(str1)).toEqual(bloomFilter.hash3(str1))
expect(bloomFilter.hash1(str1)).toBe(14)
expect(bloomFilter.hash2(str1)).toBe(43)
expect(bloomFilter.hash3(str1)).toBe(10)
const str2 = 'orange'
expect(bloomFilter.hash1(str2)).toEqual(bloomFilter.hash1(str2))
expect(bloomFilter.hash2(str2)).toEqual(bloomFilter.hash2(str2))
expect(bloomFilter.hash3(str2)).toEqual(bloomFilter.hash3(str2))
expect(bloomFilter.hash1(str2)).toBe(0)
expect(bloomFilter.hash2(str2)).toBe(61)
expect(bloomFilter.hash3(str2)).toBe(10)
})
it('должен создать массив с тремя хешированными значениями', () => {
expect(bloomFilter.getHashValues('abc').length).toBe(3)
expect(bloomFilter.getHashValues('abc')).toEqual([66, 63, 54])
})
it('должен добавить строки и возвращать `true` при проверке их наличия', () => {
people.forEach((person) => bloomFilter.insert(person))
// expect(bloomFilter.mayContain('Bruce Wayne')).toBe(true)
// expect(bloomFilter.mayContain('Clark Kent')).toBe(true)
// expect(bloomFilter.mayContain('Barry Allen')).toBe(true)
expect(bloomFilter.mayContain('Tony Stark')).toBe(false)
})
})
Запускаем тесты:
npm run test ./data-structures/__tests__/bloom-filter
Результаты:

Кэш актуальных данных
Описание
Кэш актуальных (часто используемых) данных (least recently used (LRU) cache) орган�изует (хранит) элементы таким образом, что мы можем легко определить, какие элементы используются часто, а какие - редко.
Реализация КАД включает в себя:
- конструктор
LRUCache(capacity: number), инициализирующий КАД определенного размера (capacity, положительное целое число) - метод
get(key: string), возвращающий значение по ключу (key) илиnull - метод
set(key: string, value: any), обновляющий или добавляющий значение (value) по ключу (key). При превышенииcapacityиз кэша удаляется (вытесняется) самое старое (наименее используемое) значение
Функции get и set должны выполняться за константное время O(1).
Сложность
Временная
| get | set |
|---|---|
| O(1) | O(1) |
Пространственная
O(n)
Реализация
Двусвязный список и хеш-таблица
В следующей реализации КАД мы будем использовать хеш-таблицу (см. часть 2, раздел 5) для константного (в среднем) доступа к элементам и двойной связный список (см. часть 1, раздел 2) для константного обновления и вытеснения элементов.

Начнем с реализации узла:
// data-structures/lru-cache.js
// Узел
class Node {
constructor(key, val, prev = null, next = null) {
// Ключ
this.key = key
// Значение
this.val = val
// Ссылка на предыдущий узел
this.prev = prev
// Ссылка на следующий узел
this.next = next
}
}
Теперь займемся КАД:
// КАД
export default class LRUCache {
// Конструктор принимает емкость кэша
constructor(capacity) {
// Максимальный размер кэша
this.capacity = capacity
// Кэшированные узлы
this.nodesMap = {}
// Текущий размер кэша
this.size = 0
// Головной узел
this.head = new Node()
// Хвостовой узел
this.tail = new Node()
}
}
Метод получения элемента по ключу:
// Возвращает значение по ключу
get(key) {
const node = this.nodesMap[key]
if (!node) return null
// Обновляем "приоритет" узла
this.promote(node)
return node.val
}
Метод добавления элемента в кэш:
// Добавляет узел в кэш
set(key, val) {
if (this.nodesMap[key]) {
// Обновляем значение существующего узла
const node = this.nodesMap[key]
node.val = val
this.promote(node)
} else {
// Добавляем новый узел
const node = new Node(key, val)
this.append(node)
}
}
Метод обновления приоритета узла:
/**
* Перемещает узел в конец связного списка.
* Это означает, что узел используется наиболее часто.
* Это также снижает вероятность удаления такого узла из кэша
*/
promote(node) {
this.evict(node)
this.append(node)
}
Метод добавления узла в конец связного списка:
// Перемещает узел в конец связного списка
append(node) {
this.nodesMap[node.key] = node
if (!this.head.next) {
// Первый узел
this.head.next = node
this.tail.prev = node
node.prev = this.head
node.next = this.tail
} else {
// Добавляем узел в конец
const oldTail = this.tail.prev
oldTail.next = node
node.prev = oldTail
node.next = this.tail
this.tail.prev = node
}
// Увеличиваем текущий размер кэша
this.size += 1
// Если достигнут максимальный размер кэша,
// то удаляем первый узел
if (this.size > this.capacity) {
this.evict(this.head.next)
}
}
И метод удаления узла:
// Удаляет (вытесняет) узел из кэша
evict(node) {
delete this.nodesMap[node.key]
// Уменьшаем текущий размер кэша
this.size -= 1
const prev = node.prev
const next = node.next
// Имеется только один узел
if (prev === this.head && next === this.tail) {
this.head.next = null
this.tail.prev = null
this.size = 0
return
}
// Это головной узел
if (prev === this.head) {
next.prev = this.head
this.head.next = next
return
}
// Это хвостовой узел
if (next === this.tail) {
prev.next = this.tail
this.tail.prev = prev
return
}
// Это узел в середине списка
prev.next = next
next.prev = prev
}
Полный код КАД вместе с узлом
// Узел
class Node {
constructor(key, val, prev = null, next = null) {
// Ключ
this.key = key
// Значение
this.val = val
// Ссылка на предыдущий узел
this.prev = prev
// Ссылка на следующий узел
this.next = next
}
}
// КАД
export default class LRUCache {
// Конструктор принимает емкость кэша
constructor(capacity) {
// Максимальный размер кэша
this.capacity = capacity
// Кэшированные узлы
this.nodesMap = {}
// Текущий размер кэша
this.size = 0
// Головной узел
this.head = new Node()
// Хвостовой узел
this.tail = new Node()
}
// Возвращает значение по ключу
get(key) {
const node = this.nodesMap[key]
if (!node) return null
// Обновляем "приоритет" узла
this.promote(node)
return node.val
}
// Добавляет узел в кэш
set(key, val) {
if (this.nodesMap[key]) {
// Обновляем значение существующего узла
const node = this.nodesMap[key]
node.val = val
this.promote(node)
} else {
// Добавляем новый узел
const node = new Node(key, val)
this.append(node)
}
}
/**
* Перемещает узел в конец связного списка.
* Это означает, что узел используется наиболее часто.
* Это также снижает вероятность удаления такого узла из кэша
*/
promote(node) {
this.evict(node)
this.append(node)
}
// Перемещает узел в конец связного списка
append(node) {
this.nodesMap[node.key] = node
if (!this.head.next) {
// Первый узел
this.head.next = node
this.tail.prev = node
node.prev = this.head
node.next = this.tail
} else {
// Добавляем узел в конец
const oldTail = this.tail.prev
oldTail.next = node
node.prev = oldTail
node.next = this.tail
this.tail.prev = node
}
// Увеличиваем текущий размер кэша
this.size += 1
// Если достигнут максимальный размер кэша,
// то удаляем первый узел
if (this.size > this.capacity) {
this.evict(this.head.next)
}
}
// Удаляет (вытесняет) узел из кэша
evict(node) {
delete this.nodesMap[node.key]
// Уменьшаем текущий размер кэша
this.size -= 1
const prev = node.prev
const next = node.next
// Имеется только один узел
if (prev === this.head && next === this.tail) {
this.head.next = null
this.tail.prev = null
this.size = 0
return
}
// Это головной узел
if (prev === this.head) {
next.prev = this.head
this.head.next = next
return
}
// Это хвостовой узел
if (next === this.tail) {
prev.next = this.tail
this.tail.prev = prev
return
}
// Это узел в середине списка
prev.next = next
next.prev = prev
}
}
Проверяем, что КАД работает, как ожидается
import LRUCache from '../lru-cache'
describe('LRUCache', () => {
it('должен добавить/извлечь значения в/из кэша', () => {
const cache = new LRUCache(100)
expect(cache.get('key-1')).toBeNull()
cache.set('key-1', 15)
cache.set('key-2', 16)
cache.set('key-3', 17)
expect(cache.get('key-1')).toBe(15)
expect(cache.get('key-2')).toBe(16)
expect(cache.get('key-3')).toBe(17)
expect(cache.get('key-3')).toBe(17)
expect(cache.get('key-2')).toBe(16)
expect(cache.get('key-1')).toBe(15)
cache.set('key-1', 5)
cache.set('key-2', 6)
cache.set('key-3', 7)
expect(cache.get('key-1')).toBe(5)
expect(cache.get('key-2')).toBe(6)
expect(cache.get('key-3')).toBe(7)
})
it('должен вытеснить элементы из кэша раз�мером 1', () => {
const cache = new LRUCache(1)
expect(cache.get('key-1')).toBeNull()
cache.set('key-1', 15)
expect(cache.get('key-1')).toBe(15)
cache.set('key-2', 16)
expect(cache.get('key-1')).toBeNull()
expect(cache.get('key-2')).toBe(16)
cache.set('key-2', 17)
expect(cache.get('key-2')).toBe(17)
cache.set('key-3', 18)
cache.set('key-4', 19)
expect(cache.get('key-2')).toBeNull()
expect(cache.get('key-3')).toBeNull()
expect(cache.get('key-4')).toBe(19)
})
it('должен вытеснить элементы из кэша размером 2', () => {
const cache = new LRUCache(2)
expect(cache.get('key-21')).toBeNull()
cache.set('key-21', 15)
expect(cache.get('key-21')).toBe(15)
cache.set('key-22', 16)
expect(cache.get('key-21')).toBe(15)
expect(cache.get('key-22')).toBe(16)
cache.set('key-22', 17)
expect(cache.get('key-22')).toBe(17)
cache.set('key-23', 18)
expect(cache.size).toBe(2)
expect(cache.get('key-21')).toBeNull()
expect(cache.get('key-22')).toBe(17)
expect(cache.get('key-23')).toBe(18)
cache.set('key-24', 19)
expect(cache.size).toBe(2)
expect(cache.get('key-21')).toBeNull()
expect(cache.get('key-22')).toBeNull()
expect(cache.get('key-23')).toBe(18)
expect(cache.get('key-24')).toBe(19)
})
it('должен вытеснить элемент из кэша размером 3', () => {
const cache = new LRUCache(3)
cache.set('key-1', 1)
cache.set('key-2', 2)
cache.set('key-3', 3)
expect(cache.get('key-1')).toBe(1)
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-3')).toBe(3)
cache.set('key-3', 4)
expect(cache.get('key-1')).toBe(1)
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-3')).toBe(4)
cache.set('key-4', 5)
expect(cache.get('key-1')).toBeNull()
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-3')).toBe(4)
expect(cache.get('key-4')).toBe(5)
})
it('должен обновить узел при вызове метода `set`', () => {
const cache = new LRUCache(2)
cache.set('2', 1)
cache.set('1', 1)
cache.set('2', 3)
cache.set('4', 1)
expect(cache.get('1')).toBeNull()
expect(cache.get('2')).toBe(3)
})
it('должен обновить элементы в кэше размером 3', () => {
const cache = new LRUCache(3)
cache.set('key-1', 1)
cache.set('key-2', 2)
cache.set('key-3', 3)
expect(cache.get('key-1')).toBe(1)
cache.set('key-4', 4)
expect(cache.get('key-1')).toBe(1)
expect(cache.get('key-3')).toBe(3)
expect(cache.get('key-4')).toBe(4)
expect(cache.get('key-2')).toBeNull()
})
it('должен обновить элементы в кэше размером 4', () => {
const cache = new LRUCache(4)
cache.set('key-1', 1)
cache.set('key-2', 2)
cache.set('key-3', 3)
cache.set('key-4', 4)
expect(cache.get('key-4')).toBe(4)
expect(cache.get('key-3')).toBe(3)
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-1')).toBe(1)
cache.set('key-5', 5)
expect(cache.get('key-1')).toBe(1)
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-3')).toBe(3)
expect(cache.get('key-4')).toBeNull()
expect(cache.get('key-5')).toBe(5)
cache.set('key-6', 6)
expect(cache.get('key-1')).toBeNull()
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-3')).toBe(3)
expect(cache.get('key-4')).toBeNull()
expect(cache.get('key-5')).toBe(5)
expect(cache.get('key-6')).toBe(6)
})
})
Выполняем тесты:
npm run test ./data-structures/__tests__/lru-cache
Результаты:

Упорядоченная карта
Реализация, в которой используется связный список, полезна в целях обучения, поскольку позволяет понять, как достигается время выполнения O(1) операций get и set.
Однако КАД легче реализовать с помощью объекта Map, который хранит пары "ключ-значение" и запоминает порядок добавления ключей. Мы можем хранить последний используемый элемент в конце карты за счет его удаления и повторного добавления. Элемент, находящийся в начале карты, первым вытесняется из кэша. Для проверки порядка элементов можно использовать IteratorIterable, такой как map.keys().
// data-structure/lru-cache-on-map.js
export default class LruCacheOnMap {
// Конструктор принимает размер кэша
constructor(size) {
// Размер кэша
this.size = size
// Хранилище (по сути, сам кэш)
this.map = new Map()
}
// Возвращает значение по ключу
get(key) {
const val = this.map.get(key)
if (!val) return null
// Обновляем "приоритет" элемента
this.map.delete(key)
this.map.set(key, val)
return val
}
// Добавляет элемент в кэш
set(key, val) {
// Обновляем "приоритет" элемента
this.map.delete(key)
this.map.set(key, val)
// Если кэш переполнен, удаляем первый (самый редко используемый) элемент
if (this.map.size > this.size) {
for (const key of this.map.keys()) {
this.map.delete(key)
break
}
}
}
}
Проверяем, что КАД, реализованный с помощью карты, работает, как ожидается
// data-structure/__tests__/lru-cache-on-map.test.js
import LRUCache from '../lru-cache-on-map'
describe('LRUCacheOnMap', () => {
it('должен добавить/извлечь значения в/из кэша', () => {
const cache = new LRUCache(100)
expect(cache.get('key-1')).toBeNull()
cache.set('key-1', 15)
cache.set('key-2', 16)
cache.set('key-3', 17)
expect(cache.get('key-1')).toBe(15)
expect(cache.get('key-2')).toBe(16)
expect(cache.get('key-3')).toBe(17)
expect(cache.get('key-3')).toBe(17)
expect(cache.get('key-2')).toBe(16)
expect(cache.get('key-1')).toBe(15)
cache.set('key-1', 5)
cache.set('key-2', 6)
cache.set('key-3', 7)
expect(cache.get('key-1')).toBe(5)
expect(cache.get('key-2')).toBe(6)
expect(cache.get('key-3')).toBe(7)
})
it('должен вытеснить элементы из кэша размером 1', () => {
const cache = new LRUCache(1)
expect(cache.get('key-1')).toBeNull()
cache.set('key-1', 15)
expect(cache.get('key-1')).toBe(15)
cache.set('key-2', 16)
expect(cache.get('key-1')).toBeNull()
expect(cache.get('key-2')).toBe(16)
cache.set('key-2', 17)
expect(cache.get('key-2')).toBe(17)
cache.set('key-3', 18)
cache.set('key-4', 19)
expect(cache.get('key-2')).toBeNull()
expect(cache.get('key-3')).toBeNull()
expect(cache.get('key-4')).toBe(19)
})
it('должен вытеснить элементы из кэша размером 2', () => {
const cache = new LRUCache(2)
expect(cache.get('key-21')).toBeNull()
cache.set('key-21', 15)
expect(cache.get('key-21')).toBe(15)
cache.set('key-22', 16)
expect(cache.get('key-21')).toBe(15)
expect(cache.get('key-22')).toBe(16)
cache.set('key-22', 17)
expect(cache.get('key-22')).toBe(17)
cache.set('key-23', 18)
expect(cache.get('key-21')).toBeNull()
expect(cache.get('key-22')).toBe(17)
expect(cache.get('key-23')).toBe(18)
cache.set('key-24', 19)
expect(cache.get('key-21')).toBeNull()
expect(cache.get('key-22')).toBeNull()
expect(cache.get('key-23')).toBe(18)
expect(cache.get('key-24')).toBe(19)
})
it('должен вытеснить элемент из кэша размером 3', () => {
const cache = new LRUCache(3)
cache.set('key-1', 1)
cache.set('key-2', 2)
cache.set('key-3', 3)
expect(cache.get('key-1')).toBe(1)
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-3')).toBe(3)
cache.set('key-3', 4)
expect(cache.get('key-1')).toBe(1)
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-3')).toBe(4)
cache.set('key-4', 5)
expect(cache.get('key-1')).toBeNull()
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-3')).toBe(4)
expect(cache.get('key-4')).toBe(5)
})
it('должен обновить узел при вызове метода `set`', () => {
const cache = new LRUCache(2)
cache.set('2', 1)
cache.set('1', 1)
cache.set('2', 3)
cache.set('4', 1)
expect(cache.get('1')).toBeNull()
expect(cache.get('2')).toBe(3)
})
it('должен обновить элементы в кэше размером 3', () => {
const cache = new LRUCache(3)
cache.set('key-1', 1)
cache.set('key-2', 2)
cache.set('key-3', 3)
expect(cache.get('key-1')).toBe(1)
cache.set('key-4', 4)
expect(cache.get('key-1')).toBe(1)
expect(cache.get('key-3')).toBe(3)
expect(cache.get('key-4')).toBe(4)
expect(cache.get('key-2')).toBeNull()
})
it('должен обновить элементы в кэше размером 4', () => {
const cache = new LRUCache(4)
cache.set('key-1', 1)
cache.set('key-2', 2)
cache.set('key-3', 3)
cache.set('key-4', 4)
expect(cache.get('key-4')).toBe(4)
expect(cache.get('key-3')).toBe(3)
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-1')).toBe(1)
cache.set('key-5', 5)
expect(cache.get('key-1')).toBe(1)
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-3')).toBe(3)
expect(cache.get('key-4')).toBeNull()
expect(cache.get('key-5')).toBe(5)
cache.set('key-6', 6)
expect(cache.get('key-1')).toBeNull()
expect(cache.get('key-2')).toBe(2)
expect(cache.get('key-3')).toBe(3)
expect(cache.get('key-4')).toBeNull()
expect(cache.get('key-5')).toBe(5)
expect(cache.get('key-6')).toBe(6)
})
})
Выполняем тесты:
npm run test ./data-structures/__tests__/lru-cache-on-map
Результаты:
